atomorbitaler
en orbital är kvantmekanisk förfining av Bohrs bana. I motsats till hans koncept om en enkel cirkulär bana med en fast radie är orbitaler matematiskt härledda regioner i rymden med olika sannolikheter för att ha en elektron.
ett sätt att representera elektronsannolikhetsfördelningar illustrerades i Figur 6.5.2 för 1s-orbitalen av väte. Eftersom Jacob2 ger sannolikheten för att hitta en elektron i en given volym utrymme (såsom en kubisk pikometer), är en plot av Jacob2 kontra avstånd från kärnan (r) en plot av sannolikhetstätheten. 1s-orbitalen är sfäriskt symmetrisk, så sannolikheten för att hitta en 1s-elektron vid en given punkt beror endast på dess avstånd från kärnan. Sannolikhetstätheten är störst vid r = 0 (vid kärnan) och minskar stadigt med ökande avstånd. Vid mycket stora värden på r är elektronsannolikhetstätheten mycket liten men inte noll.
däremot kan vi beräkna den radiella sannolikheten (sannolikheten att hitta en 1s elektron på ett avstånd r från kärnan) genom att lägga samman sannolikheten för att en elektron är vid alla punkter på en serie X sfäriska skal med radie r1, r2, r3,…, rx − 1, rx. I själva verket delar vi atomen i mycket tunna koncentriska skal, ungefär som skikten av en lök (del (A) i Figur \(\PageIndex{1}\)) och beräknar sannolikheten för att hitta en elektron på varje sfäriskt skal. Minns att elektronsannolikhetstätheten är störst vid r = 0 (del (b) i Figur \(\PageIndex{1}\)), Så tätheten av prickar är störst för de minsta sfäriska skalen delvis (a) i Figur \(\PageIndex{1}\). Däremot är ytan på varje sfäriskt skal lika med 4nr2, vilket ökar mycket snabbt med ökande r (del (c) i Figur \(\PageIndex{1}\)). Eftersom ytan på de sfäriska skalen ökar snabbare med ökande r än elektrons sannolikhetstätheten minskar, har plottet med radiell Sannolikhet ett maximum vid ett visst avstånd (del (d) i Figur \(\PageIndex{1}\)). Viktigast, när r är mycket liten, är ytan på ett sfäriskt skal så liten att den totala sannolikheten för att hitta en elektron nära kärnan är mycket låg; vid kärnan försvinner elektronsannolikheten (del (d) i Figur \(\PageIndex{1}\)).

för väteatomen uppträder toppen i det radiella sannolikhetsplottet vid r = 0,529 kg (52,9 pm), vilket är exakt radien beräknad av Bohr för N = 1-banan. Således är den mest sannolika radien erhållen från kvantmekanik identisk med radien beräknad av klassisk mekanik. I Bohrs modell antogs emellertid elektronen vara på detta avstånd 100% av tiden, medan det i den kvantmekaniska Schr Auddinger-modellen bara är på detta avstånd en del av tiden. Skillnaden mellan de två modellerna är hänförlig till elektronens vågliknande beteende och Heisenbergs osäkerhetsprincip.
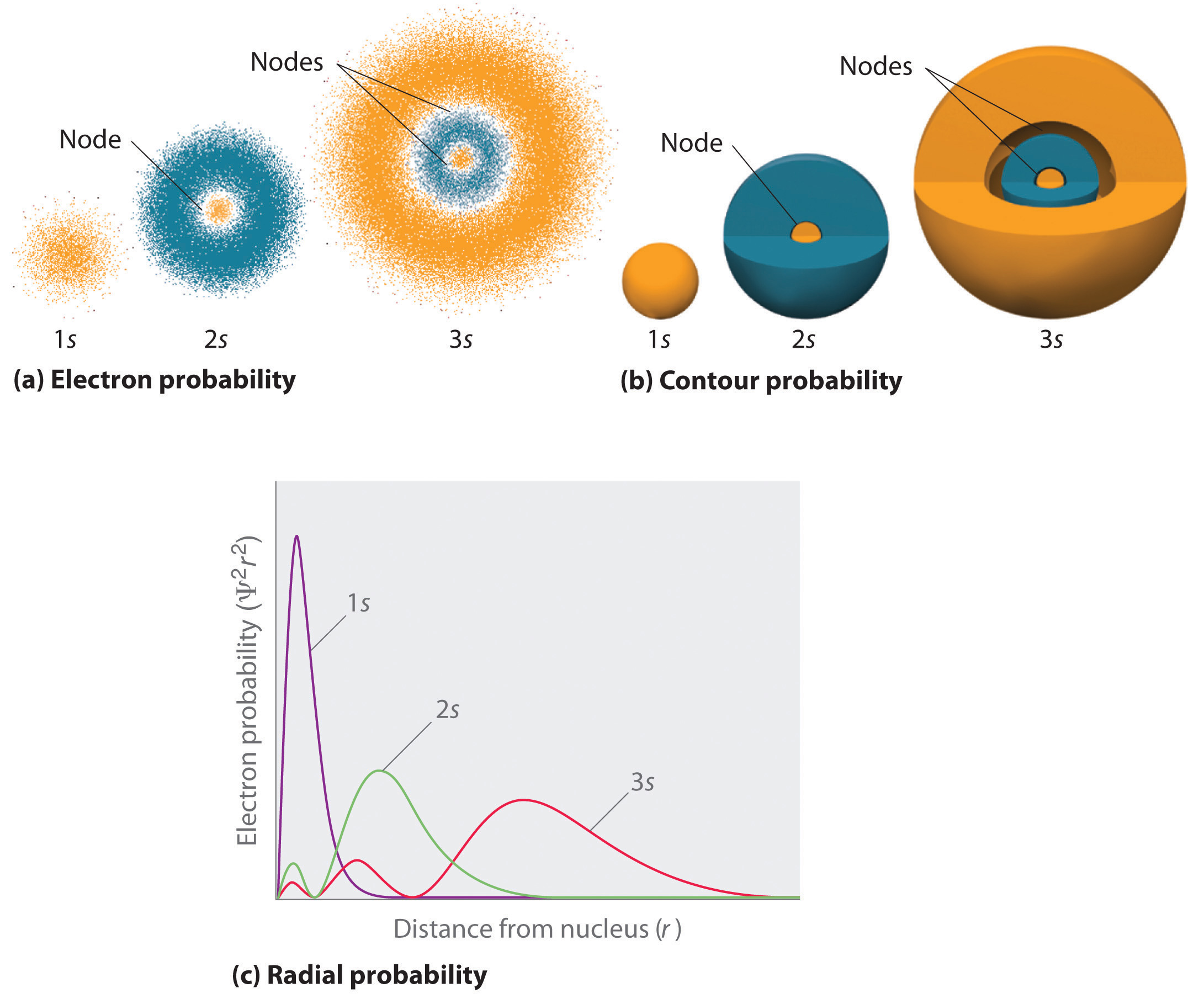
figur \(\PageIndex{2}\) jämför elektronsannolikhetstätheterna för väte 1s, 2s och 3S orbitaler. Observera att alla tre är sfäriskt symmetriska. För 2s-och 3S-orbitalerna (och för alla andra s-orbitaler också) faller elektronsannolikhetstätheten inte smidigt med ökande r. istället observeras en serie minima och maxima i de radiella sannolikhetsplottorna (del (c) i Figur \(\PageIndex{2}\)). Minima motsvarar sfäriska noder (regioner med nollelektrons Sannolikhet), som alternerar med sfäriska regioner med icke-nollelektrons Sannolikhet.