Em outras seções foi mencionado que muitas das propriedades dos sólidos, líquidos e gases pode ser contabilizado para se partimos do pressuposto de que as substâncias são feitas de átomos ou moléculas que estão em constante movimento. A lei de Boyle e as outras leis do gás deram-nos agora muito mais informações quantitativas sobre os gases, e vale a pena perguntar se, com o modelo anterior, podemos fazer previsões quantitativas de acordo com essas leis. Ao responder a esta pergunta, nós também ganharemos insights importantes sobre a natureza da temperatura e da energia do calor.

A teoria microscópica do comportamento dos gases baseada no movimento molecular é chamada de teoria cinética dos gases. Seus postulados básicos estão listados na Tabela 1:

tabela \(\PageIndex{1}\) postulados da Teoria Cinética dos Gases.

1 as moléculas de um gás são pequenas e muito distantes. A maior parte do volume que um gás ocupa é espaço vazio.

2 moléculas de gás estão em constante movimento aleatório. Assim como muitas moléculas estão se movendo em uma direção como em qualquer outra.as moléculas podem colidir entre si e com as paredes do recipiente. Colisões com as paredes são responsáveis pela pressão do gás.

4 Quando colisões ocorrem, as moléculas não perdem energia cinética, ou seja, as colisões são ditas perfeitamente elásticas. A energia cinética total de todas as moléculas permanece constante, a menos que haja alguma interferência externa com o

5 as moléculas não exercem forças atrativas ou repulsivas um sobre o outro, exceto durante o processo de colisão. Entre colisões, movem-se em linhas rectas.

a Partir deles é possível obter a seguinte expressão para a pressão de um gás, em termos das propriedades de suas moléculas:

\ Onde P, V = pressão e volume do gás

N = número de moléculas

m = massa de cada molécula

(u2)ave = média (ou média) dos quadrados de todas as velocidades moleculares. Esta velocidade quadrada média deve ser usada porque a pressão é proporcional ao quadrado da velocidade molecular, e colisões moleculares causam diferentes moléculas a ter velocidades bastante diferentes.

em vez de nos preocuparmos com o procedimento para derivar a NQA. \(\ref{1}\), Vamos inspecionar a equação e ver que as suas características gerais são tanto quanto seria de esperar. De certa forma, a capacidade de fazer isso com uma fórmula é mais útil do que a capacidade de derivá-la. Figura \(\PageIndex{1}\)

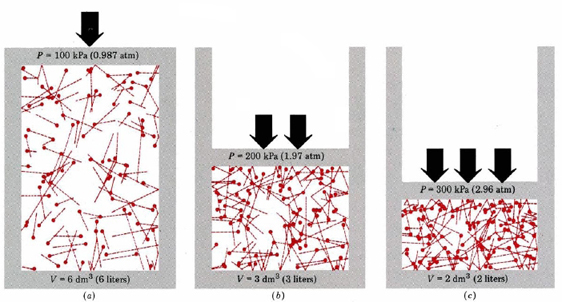em primeiro lugar, a equação diz-nos que a pressão de um gás é proporcional ao número de moléculas divididas pelo volume. Isto é mostrado graficamente na figura \(\PageIndex{1}\), onde um computador desenhou o mesmo número de moléculas de gás ocupando cada um dos três volumes diferentes. A “cauda” em cada molécula mostra o caminho exato seguido por essa molécula no microssegundo anterior—quanto maior a cauda, mais rápida a molécula estava indo. A média dos quadrados dos comprimentos da cauda é proporcional ao ave (u2)e é a mesma em todos os três diagramas. Também se assume que todas as moléculas têm massas iguais.

Como pode ver, reduzir o volume do gás aumenta o número de colisões por unidade de área nas paredes do recipiente. Cada colisão exerce força na parede; força por unidade de área é pressão, e assim o número de colisões por unidade de área é proporcional à pressão. Reduzir para metade o volume duplica a pressão, uma previsão que concorda com os fatos experimentais resumidos na lei de Boyle. A equação \(\ref{1}\) também diz que a pressão é proporcional à massa de cada molécula de gás. Mais uma vez, isto é o que nós esperaríamos. Moléculas pesadas dão um “empurrão”maior(o termo técnico para isso é impulso) contra a parede do que as leves com a mesma velocidade.

finalmente, a equação nos diz que a pressão é proporcional à média dos quadrados das velocidades moleculares. Esta dependência do quadrado da velocidade é razoável se percebermos que dobrar a velocidade de uma molécula tem dois efeitos.em primeiro lugar, a molécula pode mover-se mais longe num dado período de tempo, duplicando o número de colisões com as paredes. Isto duplicaria a pressão. Em segundo lugar, dobrar a velocidade de uma molécula duplica o impulso ou impulso de cada colisão. Isto duplica a pressão outra vez. Portanto, dobrar a velocidade de uma molécula quadruplica a pressão, e para um grande número de moléculas, P é proporcional à velocidade quadrada média.