Atomic Orbitals
an orbital is the quantum mechanical refinement of Bohr’s orbit. Em contraste com seu conceito de uma órbita circular simples com um raio fixo, orbitais são regiões matematicamente derivadas do espaço com diferentes probabilidades de ter um elétron.uma forma de representar distribuições de probabilidade de elétrons foi ilustrada na figura 6.5.2 para o orbital 1s de hidrogênio. Porque Ψ2 dá a probabilidade de encontrar um elétron em um determinado volume de espaço (como um picômetro cúbico), um gráfico de Ψ2 versus distância do núcleo (r) é um gráfico da densidade de probabilidade. O orbital 1s é esférico simétrico, então a probabilidade de encontrar um elétron 1s em qualquer ponto determinado depende apenas de sua distância do núcleo. A densidade de probabilidade é maior em r = 0 (no núcleo) e diminui de forma constante com o aumento da distância. Em valores muito grandes de r, A densidade de probabilidade de elétrons é muito pequena, mas não zero.
Em contraste, podemos calcular a radial da probabilidade (probabilidade de encontrar um electrão 1s a uma distância r do núcleo) somando-se as probabilidades de um elétron estar em todos os pontos em uma série de x cascas esféricas de raio r1, r2, r3,…, rx − 1, rx. Com efeito, estamos dividindo o átomo em conchas concêntricas muito finas, muito como as camadas de uma cebola (parte (a) na figura \(\PageIndex{1}\)), e calculando a probabilidade de encontrar um elétron em cada concha Esférica. Lembre-se que a densidade de probabilidade de elétrons é maior em r = 0 (parte (b) Na Figura \(\PageIndex{1}\)), de modo que a densidade de pontos é maior para as menores conchas esféricas na Parte (A) Na Figura \(\PageIndex{1}\). Em contraste, a área de superfície de cada concha esférica é igual a 4nr2, o que aumenta muito rapidamente com o aumento r (parte (C) na figura \(\PageIndex{1}\)). Como a área de superfície das Conchas esféricas aumenta mais rapidamente com o aumento de R do que a densidade de probabilidade dos elétrons diminui, o gráfico de probabilidade radial tem um máximo a uma determinada distância (Parte (d) na figura \(\PageIndex{1}\)). O mais importante, quando r é muito pequeno, a área de superfície de uma concha esférica é tão pequena que a probabilidade total de encontrar um elétron perto do núcleo é muito baixo; o núcleo, o elétron probabilidade desaparece (parte (d) na Figura \(\PageIndex{1}\)).

Para o átomo de hidrogênio, o pico na radial probabilidade trama ocorre em r = 0.529 Å (52.9 pm), que é exatamente o raio calculado por Bohr para n = 1 órbita. Assim, o raio mais provável obtido da mecânica quântica é idêntico ao raio calculado pela mecânica clássica. No modelo de Bohr, no entanto, o elétron foi assumido para estar a esta distância 100% do tempo, enquanto no modelo de mecânica quântica de Schrödinger, ele está a esta distância apenas alguns do tempo. A diferença entre os dois modelos é atribuível ao comportamento ondulatório do elétron e o princípio da incerteza de Heisenberg.
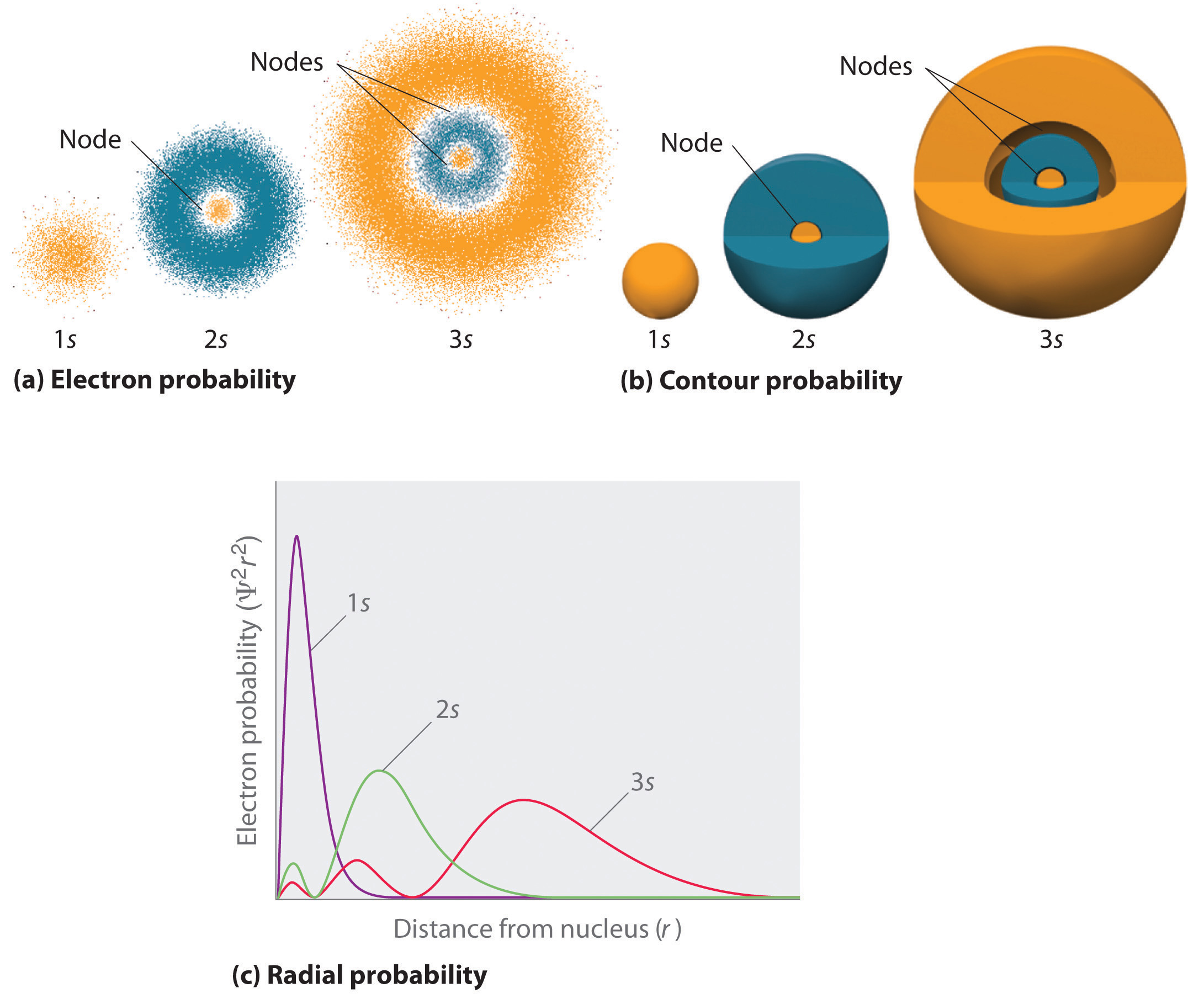
figura \(\PageIndex{2}\) compara as densidades de probabilidade dos elétrons para os orbitais de hidrogênio 1s, 2s e 3s. Note que todos os três são esféricos simétricos. Para os orbitais 2s e 3s, no entanto (e para todos os outros orbitais s também), a densidade de probabilidade de elétrons não cai suavemente com o aumento R. em vez disso, uma série de mínimos e máximos são observados nos gráficos de probabilidade radial (parte c) na figura \(\Pagindex{2}\). Os mínimos correspondem a nós esféricos (regiões de probabilidade de elétrons zero), que alternam com regiões esféricas de probabilidade de elétrons não-zero.