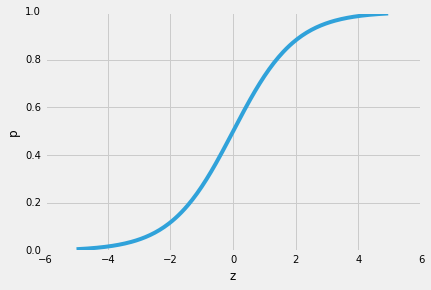
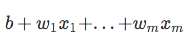tak więc, jedną z ładnych właściwości regresji logistycznej jest to, że funkcja esicy wyświetla warunkowe prawdopodobieństwa przewidywania, prawdopodobieństwa klasy. Jak to działa?Zacznijmy od tak zwanego „ilorazu szans” p / (1 – p), który opisuje stosunek między prawdopodobieństwem wystąpienia pewnego, dodatniego zdarzenia a prawdopodobieństwem jego wystąpienia-gdzie dodatnie odnosi się do „zdarzenia, które chcemy przewidzieć”, tj. p(y=1 | x).
(zauważ, że regresja logistyczna jest specjalnym rodzajem funkcji esicy, esicy logistycznej; istnieją inne funkcje esicy, na przykład styczna hiperboliczna).
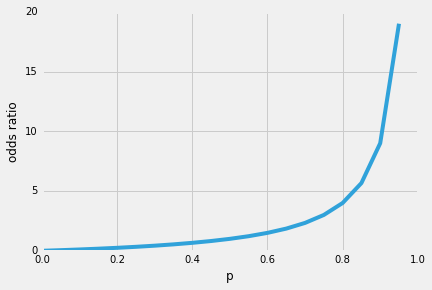
więc im bardziej prawdopodobne jest, że wystąpi zdarzenie dodatnie, tym większy jest stosunek szans.Teraz, jeśli weźmiemy logarytm naturalny tego stosunku kursów, log-odds lub funkcji logit, otrzymamy następujący
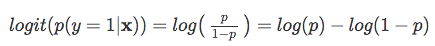
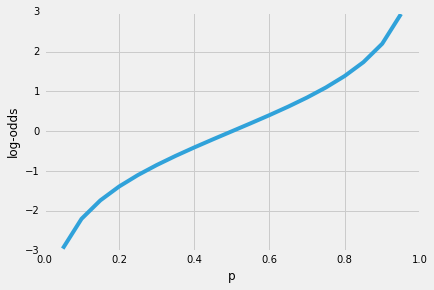

następnie użyjmy tej transformacji loga do modelowania zależności między naszymi zmiennymi objaśniającymi a zmienną docelową:
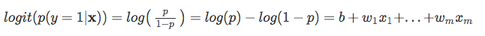
| teraz pamiętaj, że nie próbujemy przewidzieć właściwej części powyższego równania, ponieważ *p(y = 1 | X)* jest tym, co naprawdę nas interesuje. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
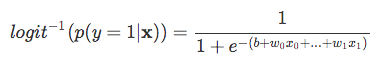
| which returns the class probabilities *p(y=1 | x)* from the inputs |