prawo Boyle ’ a
Robert Boyle (1627 – 1691), angielski chemik, jest powszechnie uważany za jednego z założycieli nowoczesnej eksperymentalnej nauki chemii. Odkrył, że podwojenie ciśnienia zamkniętej próbki gazu przy zachowaniu stałej temperatury spowodowało zmniejszenie objętości gazu o połowę. Prawo Boyle ’ a mówi, że objętość danej masy gazu zmienia się odwrotnie z ciśnieniem, gdy temperatura jest utrzymywana na stałym poziomie. Zależność odwrotna jest opisana w ten sposób. Jak jedna zmienna zwiększa wartość, druga zmienna maleje.
Co Się Dzieje? Cząsteczki gazu poruszają się i znajdują się w pewnej odległości od siebie. Wzrost ciśnienia popycha cząsteczki bliżej siebie, zmniejszając objętość. Jeśli ciśnienie jest zmniejszone, gazy mogą swobodnie poruszać się w większej objętości.

matematycznie prawo Boyle ’ a można wyrazić równaniem:
\
\(k\) jest stałą dla danej próbki gazu i zależy tylko od masy gazu i temperatury. Poniższa tabela przedstawia dane dotyczące ciśnienia i objętości dla określonej ilości gazu w stałej temperaturze. Trzecia kolumna przedstawia wartość stałej \(\left (k \right)\) dla tych danych i jest zawsze równa ciśnieniu pomnożonemu przez objętość. Gdy jedna ze zmiennych się zmienia, druga zmienia się w taki sposób, że iloczyn \(P \razy V\) zawsze pozostaje taki sam. W tym konkretnym przypadku stała ta wynosi \(500\: \ text{atm} \ cdot \ text {mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
wykres danych w tabeli dalej ilustruje odwrotną relację natury prawa Boyle ’ a (patrz rysunek poniżej). Objętość jest wykreślana na osi \(x\), z odpowiednim ciśnieniem na osi \(y\).
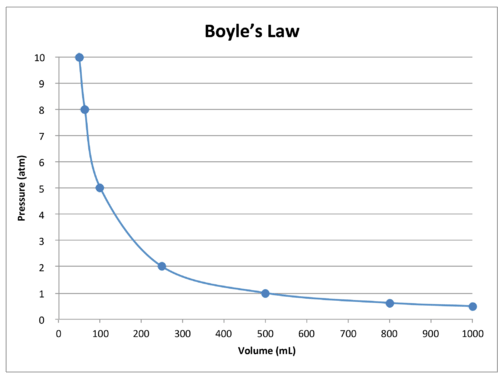
Używamy \(P_1\) i \(V_1\) do oznaczenia początkowego ciśnienia i początkowej objętości gazu. Po dokonaniu zmiany, \(P_2\) i \(V_2\) oznaczają ciśnienie końcowe i objętość. Matematyczna zależność prawa Boyle ’ a staje się:
\
równanie to może być użyte do obliczenia dowolnej z czterech wielkości, jeśli pozostałe trzy są znane.
przykład \(\PageIndex{1}\)
Próbka gazu tlenowego ma objętość \(425 \: \text{mL}\), gdy ciśnienie jest równe \(387 \: \ text{kPa}\). Gaz może rozwinąć się do kontenera \(1.75 \: \text{L}\). Oblicz nowe ciśnienie gazu.
rozwiązanie
Krok 1: Wymień znane ilości i zaplanuj problem.
znany
- \(P_1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1.75 \: \text{L} = 1750 \: \text{mL}\)
nieznany
- \(P_2 =? \ : \ text{kPa}\)
użyj prawa Boyle ’ a do rozwiązania nieznanego ciśnienia \(\left( P_2 \right)\). Ważne jest, aby dwa tomy (\(V_1\) i \(V_2\)) były wyrażone w tych samych jednostkach, więc \(V_2\) zostało przekonwertowane na \(\text{mL}\).
Krok 2: Rozwiąż.
najpierw przestawiamy równanie algebraicznie do rozwiązania dla \(P_2\).
\
teraz zastąp znane wielkości do równania i rozwiąż.
\
krok 3: pomyśl o swoim wyniku.
objętość wzrosła do nieco ponad 4 razy swojej pierwotnej wartości, a więc ciśnienie jest zmniejszone o około jedną czwartą. Ciśnienie jest w \(\text{kPa}\), a wartość ma trzy znaczące cyfry. Należy pamiętać, że wszelkie jednostki ciśnienia lub objętości mogą być używane tak długo, jak są one spójne przez cały problem.