Purplemath
in de wiskunde is een “identiteit” een vergelijking die altijd waar is. Deze kunnen” triviaal “waar zijn, zoals” x = x “of nuttig waar, zoals de Stelling van Pythagoras” a2 + b2 = c2 ” voor rechthoekige driehoeken. Er zijn tal van trigonometrische identiteiten, maar de volgende zijn degene die je waarschijnlijk zult zien en gebruiken.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Basic en de stemming van Pythagoras Identiteiten
Affiliate
Merk op hoe een “co-(iets)”trig verhouding is altijd de reciproke van een aantal “niet-co” ratio. U kunt dit feit gebruiken om u te helpen recht te houden dat cosecant gaat met sinus en secant gaat met cosinus.
de volgende (in het bijzonder de eerste van de drie hieronder) worden “Pythagoras” identiteiten genoemd.
sin2 (t) + cos2(T) = 1
tan2(T) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
advertentie
merk op dat de drie identiteiten vooral squaring en het nummer 1 omvatten. Je kunt de Pythagoras-Therom relatie duidelijk zien als je kijkt naar de eenheidscirkel, waar de hoek t is, de” tegenovergestelde “kant is sin(t) = y, de” aangrenzende ” kant is cos(t) = x, en de hypotenusa is 1.
we hebben extra identiteiten gerelateerd aan de functionele status van de trig ratio ‘ s:
sin(–t) = –sin(t)
cos(–t) = cos(t)
tan(–t) = –tan(t)
merk in het bijzonder op dat sinus en raaklijn oneven functies zijn, die symmetrisch zijn over de oorsprong, terwijl cosinus een even functie is, die symmetrisch is over de y-axis. Het feit dat je het “min” teken van het argument buiten kunt nemen (voor sinus en raaklijn) of het volledig kunt elimineren (voor cosinus) kan nuttig zijn bij het werken met ingewikkelde uitdrukkingen.
hoek-som en-verschil identiteiten
sin(α) = sin(α) cos(β) + cos(α) sin(β)
sin(α) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α) = cos(α) cos(β) + sin(α) sin(β)
in de bovenstaande identiteiten worden de hoeken overigens aangeduid met Griekse letters. De a-letter, “α”, wordt” alfa “genoemd, wat wordt uitgesproken als”AL-fuh”. De letter b-type, “β”, wordt” beta “genoemd, wat uitgesproken wordt als”BAY-tuh”.
inhoud gaat verder onder
dubbele-hoek identiteiten
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Halfhoek identiteiten
p>de bovenstaande identiteiten kunnen opnieuw worden aangegeven door elke zijde te kwadrateren en alle hoekmetingen te verdubbelen. De resultaten zijn als volgt::
Affiliate

Sum Identities
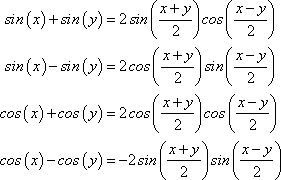
Product Identities
Affiliate
U zal worden met behulp van al deze identiteiten, of bijna, voor het aantonen van andere goniometrische identiteiten en voor het oplossen van goniometrische vergelijkingen. Echter, als je verder gaat met het bestuderen van calculus, besteed dan bijzondere aandacht aan de aangepaste sinus en cosinus halfhoek identiteiten, want je zult ze veel gebruiken in integrale calculus.
URL: https://www.purplemath.com/modules/idents.htm