Deze sectie behandelt:

• Inleiding tot Stuksgewijze Functies
• Evaluatie Stuksgewijze Functies
• Grafische Stuksgewijze Functies
• Hoe om te Vertellen als een Stuksgewijze Functie is Continu of Niet-Continu
• het Verkrijgen van Vergelijkingen van Stuksgewijze Functie Grafieken
• Absolute Waarde als een Stuksgewijze Functie
• Transformaties van Stuksgewijze Functies
• Piecewise Functie Word Problemen
• Meer Praktijk

Stuksgewijze functies (of stuksgewijze functies) zijn slechts wat ze zijn genoemd: stukken van verschillende functies (sub-functies) allemaal op één grafiek. De makkelijkste manier om er aan te denken is als je meer dan één functie op een grafiek tekent, en je gewoon delen van de functies wiste waar ze niet horen te zijn (langs de \(x\)’s); ze zijn anders gedefinieerd voor verschillende intervallen van \(x\). \(y\) is anders gedefinieerd voor verschillende waarden van \(x\); we gebruiken de \(x\) om op te zoeken in welk interval het zit, zodat we kunnen achterhalen wat de \(y\) moet zijn.

merk op dat er een voorbeeld is van de inverse van een stuksgewijze functie hier in de sectie Inverses of Functions.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Er zijn andere manieren om dit weer te geven, zoals het gebruik van een “voor” in plaats van een “ALS”, en het gebruik van komma ‘ s of semi-dubbele punten in plaats van de “als”.) domein: \(\mathbb{R},\,\,\, \ text{or}\,\, \ left ({- \infty, \ infty } \ right)\) bereik: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

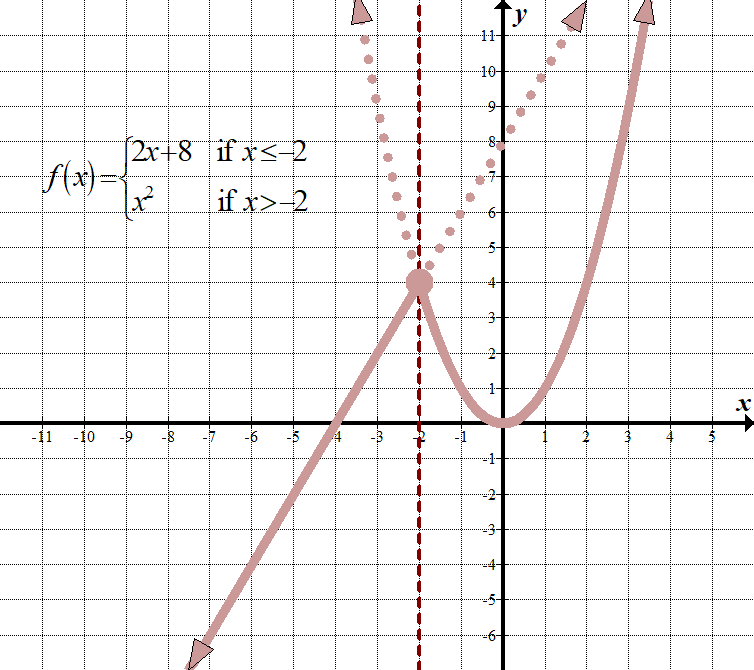wat dit middelen is voor elke \(x\) kleiner dan of gelijk aan -2, we moeten de lijn \(2x+8\) grafieken, alsof het de enige functie op de grafiek is. Voor elke \(x\) waarde groter dan -2, moeten we grafiek \({{x}^{2}}\), alsof het de enige functie op de grafiek. Dan moeten we ons ontdoen van de onderdelen die we niet nodig hebben. Vergeet niet dat we nog steeds de oorsprong gebruiken als referentiepunt voor beide grafieken!

zie je hoe de verticale lijn \(x=-2\) fungeert als een “grens” tussen de twee grafieken?

merk op dat het punt \((-2,4)\) een gesloten cirkel heeft. Technisch gezien zou het alleen tot de functie \(2x+8\) moeten behoren, omdat die functie het teken kleiner dan of gelijk heeft, maar omdat het punt ook op de grafiek \({{x}^{2}}\) staat, kunnen we gewoon een gesloten cirkel gebruiken alsof het op beide functies voorkomt. Zie je, niet zo slecht, toch?

stuksgewijze functies evalueren

soms krijgt u stuksgewijze functies en wordt u gevraagd deze te evalueren; met andere woorden, Zoek de \(y\) waarden wanneer je een \(x\) waarde krijgt. Laten we dit doen voor \(x=-6\) en \(x=4\) (zonder de grafiek te gebruiken). Hier is de functie weer:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ als }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ als }x>-2\end{align} \right.\)

We willen eerst kijken naar de Voorwaarden aan de rechterkant, om te zien waar onze \(x\) is. Als \(x=-6\), weten we dat het minder is dan -2, dus sluiten we onze \(x\) alleen aan op \(2x+8\). \(f (x)\) of \(y\) is \((2)(-6)+8=-4\). We geven niet eens om de \(\boldsymbol{{x}^{2}}\)! Zo makkelijk is het. U kunt ook zien dat we dit correct hebben gedaan met behulp van de grafiek hierboven.

Probeer nu \(x=4\). We kijken eerst naar rechts, en zien dat onze \(x\) groter is dan -2, dus steken we hem in de \({{x}^{2}}\). (We kunnen deze keer gewoon de \(2x+8\) negeren.) \(f (x)\) of \(y\) is \({{4}^{2}}=16\).

Graphing Stukswise Functions

u zult waarschijnlijk gevraagd worden om stukswise functions te grafieken. Soms bevatten de grafieken functies die niet continu of discontinu zijn, wat betekent dat je je potlood in het midden van de grafiek moet pakken wanneer je hem tekent (zoals een sprong!). Continue functies betekent dat je nooit je potlood hoeft op te pakken als je ze van links naar rechts tekent.

en onthoud dat de grafieken alleen echte functies zijn als ze de verticale lijntest doorstaan.

laten we deze stuksgewijze functies tekenen en bepalen of ze continu of niet-continu zijn. Merk op hoe we elke functie tekenen alsof het de enige is, en dan “wissen” de delen die niet nodig zijn. We krijgen ook het domein en bereik zoals we hier in de algebraïsche functies sectie hebben gedaan.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
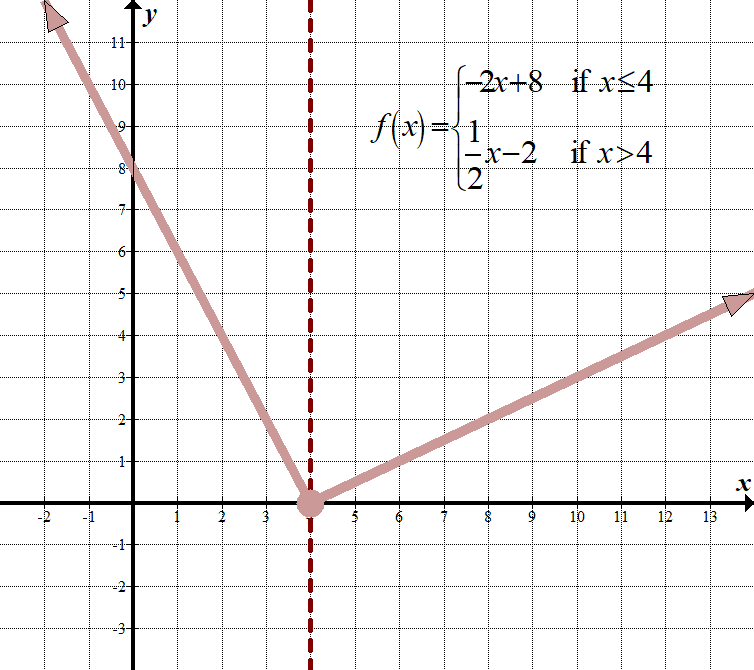\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

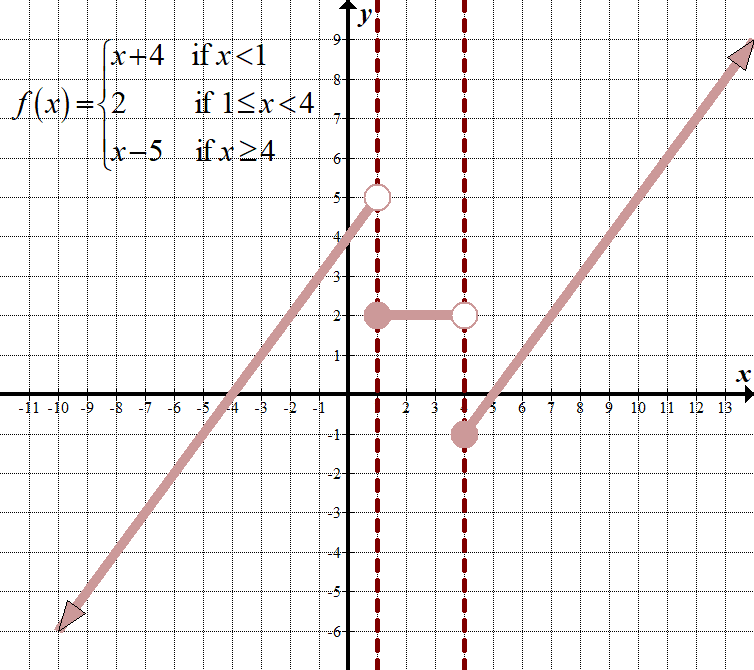We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: Hier is de grafiek:

Om de stuksgewijze functie \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{als }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als 1 }\le x<4\\-5+x\,\,\,\,\,\text{als }x\ge 4\end{array} \right.\) in de rekenmachine kun je de functie op drie regels invoeren door de functie in elk interval te delen door een “testongelijkheid” van dat interval (en let op haakjes!). de reden dat we delen door de intervallen of ongelijkheden is omdat de calculator Een 1 retourneert als de ongelijkheid(zoals \(x<1\)) Waar is; bijvoorbeeld, \((x+4)\) eindigt gewoon \((x+4)/(1)\) wanneer \(x<1\). Als \(x \ ge 1\), delen we door 0, dus er wordt niets getekend. Hier is wat we in de rekenmachine kunnen zetten: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {x+4} \right)/\left( {x<1} \right)\\{{Y}_{2}}=\left( 2 \right)/\left( {x\ge 1\text{ en }x<4} \right)\\{{Y}_{3}}=\left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (Merk op dat u dit op één lijn door het vermenigvuldigen van de voorwaarden in plaats van het verdelen, en het gebruik van plustekens tussen elk van de drie functies/intervallen: \(\displaystyle {{Y}_{1}}=\left( {x+4} \right)\left( {x<1} \right)+\left( 2 \right)\left( {x\ge 1\text{ and }X<4} \right)+\left( {-5+x} \right)\left( {x\ge 4} \right)\).) Hier zijn de toetsaanslagen voor het gebruik van drie regels. Merk op dat je 2e wiskunde (TEST) gebruikt om bij het scherm te komen dat de \(\le \), \(\ge \), enzovoort heeft. Bijvoorbeeld, 2e wiskunde 6 krijgt je \(\le \). Gebruik 2de wiskunde (TEST), rechts naar logica, dan 1, voor de “en” in \({{y}_{2}}\).

hoe te vertellen of een stuksgewijze grafiek continu of niet-continu is

om te vertellen of een stuksgewijze grafiek continu of niet-continu is, kunt u kijken naar de grenspunten en kijk of het \(Y\) punt op elk van hen hetzelfde is. (Als de \(y\) ‘ s anders waren, zou er een “sprong” in de grafiek zijn!)

laten we dit proberen voor de functies die we hierboven hebben gebruikt:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the “boundary point”: \(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) Sinds \(0=0\) is deze stuksgewijze functie continu.
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als 1 }\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\text{als }x\ge 4\end{array} \right.\)	laten we de eerste twee delen van de functie controleren. Opmerking in het tweede deel is \(y\) altijd 2: \(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) sinds \(5\ne 2\), kunnen we hier stoppen, en merk op dat deze stuksgewijze functie niet continu is. Als de \(y\)’s gelijk waren, zouden we er één moeten gaan om het volgende grenspunt op \(x=4\) te controleren.

het verkrijgen van vergelijkingen uit stuksgewijze functiegrafieken

u kan worden gevraagd om een stuksgewijze functie te schrijven, gegeven een grafiek. Nu we weten wat stuksgewijze functies zijn allemaal over, het is niet zo slecht!

om te bekijken hoe vergelijkingen uit lineaire grafieken verkregen kunnen worden, zie vergelijkingen van een lijn verkrijgen, en uit kwadraten, zie een kwadratische vergelijking vinden uit punten of een grafiek.

Hier zijn de grafieken, met uitleg over hoe ze hun stuksgewijze vergelijkingen kunnen afleiden:

Piecewise Function Graph	Procedure to get Function
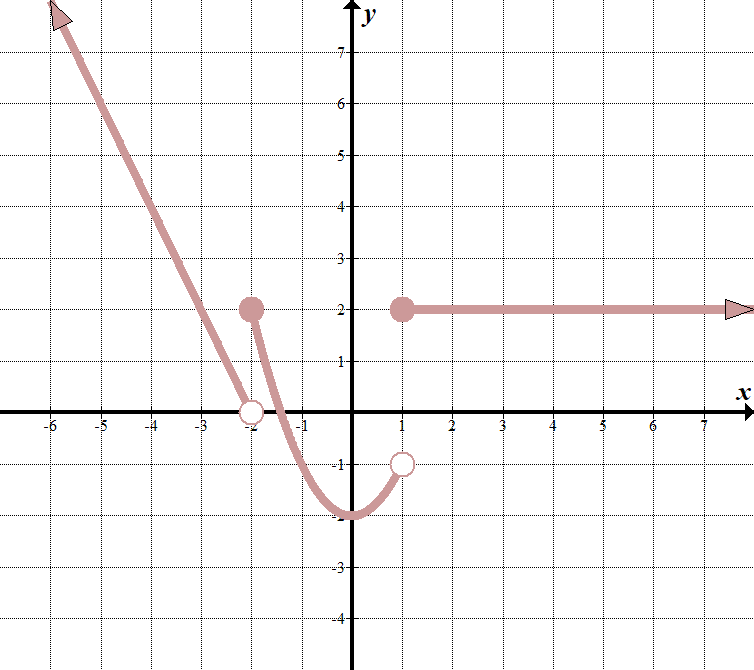	We see that our “boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\text{als }x<-2\\\tekst{ }……\,\,\,\,\,\,\,\,\text{als }-\text{2 }\le x<1\\\tekst{ }……\,\,\,\,\,\,\,\,\text{als }x\ge 1\end{array} \right.\) We kunnen twee punten \((-2,0)\) en \((-3,2)\) op de meest linkse lijn kiezen om de vergelijking \(y=-2x-4\) te krijgen. de middelste functie is \(y = {{x}^{2}}-2\), en de meest rechtse functie is alleen de horizontale lijn \(y = 2\). dus is de stuksgewijze functie: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x-4\,\,\,\,\,\,\,\text{als }x<-2\\\text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{als }-\text{2}\le x<1\\\tekst{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }x\ge 1\end{array} \right.\)
	we zien dat onze” grenslijn ” op \(x=5\) ligt. Aangezien de lijnen elkaar ontmoeten op \((5,4)\), maakt het niet uit waar we het \(\le \) of \(\ge \) teken zetten; we kunnen het niet op beide plaatsen plaatsen, anders zou het geen functie zijn. We hebben tot nu toe: \(\displaystyle f \ left (x \ right)= \ left\ {\begin{array}{l} \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x<5 \ \ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x \ ge 5 \ end{array} \ right.\) nogmaals, we moeten elke lijn apart bekijken om hun vergelijkingen te bepalen. We kunnen 2 punten van elke lijn nemen om deze te krijgen, of afleiden van hellingen en \(y\)–Onderscheppingen; de stuksgewijze functie is: \(\displaystyle f \ left (x \ right)= \ left\ {\begin{array}{l} \ frac{6}{5}x-2\,\,\,\,\,\,\,\tekst{if }x<5 \ \ \ frac{2}{5}x+2\,\,\,\,\,\,\,\text{if }x \ ge 5 \ end{array} \ right.\)

Absolute waarde als stuksgewijze functie

We kunnen absolute waardefuncties als stuksgewijze functies schrijven – het is echt cool! Misschien wilt u het oplossen van Absolute Waardevergelijkingen en ongelijkheden bekijken voordat u verder gaat met dit onderwerp.

laten we zeggen dat we de functie \(f\left( x \right)=\left| x \right|\) hebben. Van wat we eerder geleerd hebben, weten we dat wanneer \(x\) positief is, aangezien we de absolute waarde nemen, het nog steeds gewoon \(x\) zal zijn. Maar als \(x\) negatief is, als we de absolute waarde nemen, moeten we het tegenovergestelde nemen (ontkennen), omdat de absolute waarde positief moet zijn. Logisch? Dus, bijvoorbeeld, als we \(|5|\) hadden, nemen we gewoon wat er in het absolute teken zit, omdat het positief is. Maar voor \(|-5/\) moeten we het tegenovergestelde (negatief) nemen van wat er in de absolute waarde zit om het \(\displaystyle 5\,\,\,(-\,-5=5)\).

Dit betekent dat we deze absolute waardefunctie als stuksgewijze functie kunnen schrijven. Merk op dat we het “keerpunt” of “grenspunt” kunnen krijgen door wat zich binnen de absolute waarde bevindt in te stellen op 0. Dan zullen we ofwel de oorspronkelijke functie gebruiken, of de functie negeren, afhankelijk van het teken van de functie (zonder de absolute waarde) in dat interval.

bijvoorbeeld, we kunnen \(\displaystyle \left| x \right|\text {} = \ left\ {\begin{array}{l}x\,\,\,\,\,\,\,\,\,\tekst{if }x \ ge 0\\ – x\,\,\,\,\,\text{if }x<0 \ end{array} \ right.\). Merk ook op dat, als de functie continu is (er is geen “sprong”) op het grenspunt, het niet uitmaakt waar we de “kleiner dan of gelijk aan” (of “groter dan of gelijk aan”) tekens plaatsen, zolang we ze niet herhalen! We kunnen ze niet herhalen omdat we theoretisch geen twee waarden van \(y\) voor dezelfde \(x\) kunnen hebben, anders zouden we geen functie hebben.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the “boundary line”. We doen dit door in te stellen wat er in de absolute waarde zit op 0, en dan op te lossen voor \(\boldsymbol{x}\). als \(2x+3\ge 0\), krijgen we \(\displaystyle x\ge -\frac{3}{2}\) (eigenlijk kunnen we de \(\ge \) houden als we oplossen). Als \(2x+3\) positief is, nemen we het gewoon “zoals het is”, maar als het negatief is, moeten we het geheel ontkennen. daarom is de stuksgewijze functie: \(\displaystyle \ left / {2x+3} \ right / = \left\ {\begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{if }x \ ge – \ frac{3}{2} \ text { } \\ – 2x-3\,\,\,\,\,\text{if }x< – \ frac{3}{2} \ end{array} \ right.\) probeer het-het werkt!
\(f\left( x \right)=\left| {{{x}^{2}}-4} \right|\)	laten we eerst de” boundary line(s) ” vinden; we stellen de absolute waarde in op 0. als \({{x}^{2}}-4 \ ge 0\), krijgen we \(x\le -2\) of \(x\ge 2\) (Probeer een aantal getallen!). Als \({{x}^{2}}-4\) positief is, nemen we het gewoon “zoals het is”, maar als het negatief is, moeten we het ontkennen. De stuksgewijze functie is: \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\text{als }x\le -2\\4-{{x}^{2}}\,\,\,\,\,\text{als }-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\text{als }x\ge 2\text{ }\end{array} \right.\) of \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\text{als }x\le -2\text{ }\,\,\text{of}\,\,\text{ }x\ge 2\\4-{{x}^{2}}\,\,\,\,\,\,\,\text{als }-2<x<2\end{array} \right.\) nogmaals (aangezien de functie continu is), maakt het echt niet uit waar we de \(\le\) en \(\ge\) hebben (in tegenstelling tot \(<\) en \(>\)), zolang we ze maar niet herhalen.
\(f\left( x \right)=2x+\left| {x+2} \right|\)	Dit is een beetje lastiger, omdat we een \(x\) binnen en buiten de absolute waarde hebben. Voor de “grenslijn” gebruiken we alleen wat zich binnen de absolute waarde bevindt. als \(x+2\ge 0\), krijgen we \(x\ge -2\). Maar voor de stuksgewijze functie, moeten we de hele functie gebruiken, inclusief het deel dat buiten de absolute waarde ligt. Dus, de stuksgewijze functie is: \(\displaystyle 2x+ \ left / {x + 2} \ right / =\left\ {\begin{array}{l}2x + x+2\,\,\,\,\,\tekst{if }x \ ge -2\ \ 2x-x-2\,\,\,\,\,\text{if }x<-2 \ end{array} \ right.\) laten we vereenvoudigen: \(\displaystyle 2x+\left|{x+2} \right / =\left\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\tekst{if }x \ ge -2\ \ x-2\,\,\,\,\,\,\,\,\,\,\text{if }x<-2 \ end{array} \ right.\) probeer een aantal waarden kleiner dan en groot dan -2; ze zouden moeten werken!
\(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\)	deze kan het best worden opgelost met een tekendiagram omdat we een kwadratische hebben en we moeten weten waar de functie positief en negatief is. eerst factor je de kwadratische functie binnen de absolute waarde naar \(\left ({x-5}\right) \left ({x+1}\right)\). Gebruik dan een tekendiagram om te zien waar de factoren positief en negatief zijn, en vergeet niet dat waar de factoren positief zijn, we de functie gebruiken “zoals ze is”, en waar de factoren negatief zijn, we de functie ontkennen: \(\displaystyle \left| {{{x}^{2}}-4x-5} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }x\le -1\,\,\,\,\tekst{of}\,\,\,\,x\ge 5\\-\left( {{{x}^{2}}-4x-5} \right)\,\,\,\,\text{als }-1<x<5\text{ }\end{array} \right.\)
\(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\)	Dit is een rationele functie omdat er een variabele in de noemer zit. wanneer \(x+2\ge 0\), krijgen we \(\displaystyle x\ge -2\). Als \(x+2\) positief is, kunnen we gewoon “zoals het is”, maar als het negatief is, hebben we om te ontkennen wat in de absolute waarde: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}\frac{{x+2}}{{x+2}}\,\,\,\,\,\,\,\,\,\text{als }x\ge -2\\\frac{{-x-2}}{{x+2}}\,\,\,\,\,\,\text{als }x<-2\end{array} \right.\). Maar we moeten voorzichtig zijn, omdat \(x\ne 2\) (domeinbeperking: de noemer zou 0 zijn). daarom is de stuksgewijze functie: \(\displaystyle\frac {{\left / {x + 2} \ right/}} {{x + 2}}= \ left\ {\begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\tekst{if }x>-2\\-1\,\,\,\,\,\,\text{if }x<-2 \ end{array} \ right.\).

u kunt ook worden gevraagd om een absolute waardegrafiek te nemen en deze als stuksgewijze functie te schrijven:

Absolute Value Graph	Method to get Piecewise Function
	We see that our “boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Dit is omdat om de grenslijn met een absolute waarde functie te krijgen, we instellen wat er in de absolute waarde op 0, en oplossen voor \(x\)). wanneer \(x>0\), kunnen we zien dat de vergelijking van de lijn \(y=2x-2\) is. Wanneer \(x<0\), is de vergelijking \(y=2x-2\). We kunnen dit schrijven als een stuksgewijze functie: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\text{if }x>0\\ – 2x-2\,\,\,\text{if }x \ le 0 \ end{array} \ right.\) We kunnen dit ook schrijven als een getransformeerde absolute waarde functie: \(y=2\left| x \right|-2\) of \(y=\left| {2x} \right|-2\) (aangezien 2 positief is, kan het binnen of buiten de \(\left| {\,\,} \right|\)). (Dit is logisch want als wat in de \(\left| {\,\,} \right|\) \(> 0\) zit, gebruiken we de reguliere functie \(y=2x-2\), en als wat in de \(< 0\) zit, negeren we het absolute waardedeel om het \(y=-\left( {2x}) \right) -2\)).
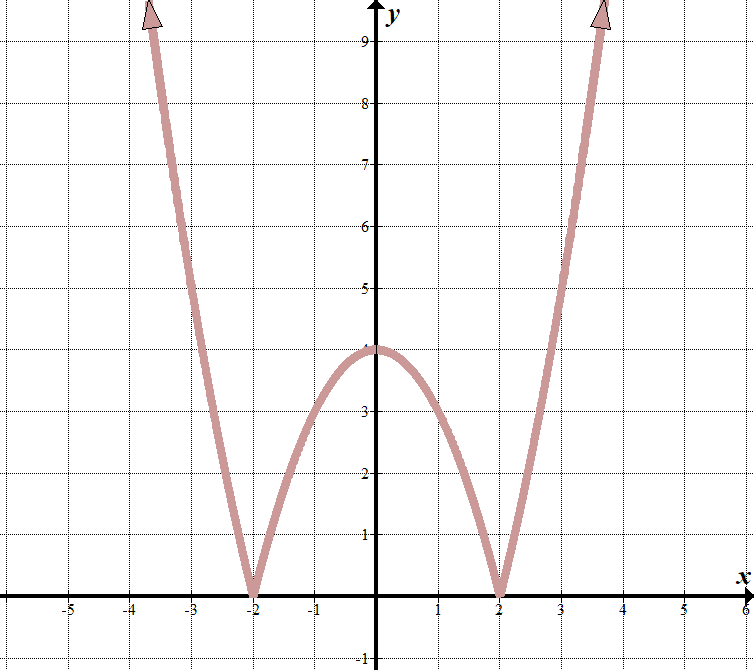	we zien dat onze “grenslijnen” op \(x=2\) en \(x=-2\) liggen, dus wat er in het absolute waardeteken zit moet factoren hebben van \(x-2\) en \(X+2\). wanneer \(x<-2\) of \(x>2\), kunnen we zien dat de grafiek eruit ziet als het normale deel van de grafiek \(y = {{x}^{2}}-4\). (Ik bedacht dit door het kennen van de factoren, en het nemen van een goede gok!) Wanneer \(-2<x<2\), wordt de vergelijking omgedraaid, of ontkend (omgedraaid over de \(x\)-as). We kunnen dit schrijven als een stuksgewijze functie: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{als }x<-2\text{ of }x>2\\-{{x}^{2}}\text{+ 4}\,\,\,\,\,\,\text{als }-2\le x\le 2\end{array} \right.\) We kunnen zien dat dit begon met een getransformeerde kwadratische functie \(y={{x}^{2}}-4\) met een absolute waarde eromheen, omdat alle \(y\) waarden positief zijn: \(y=\left| {{{x}^{2}}-4} \right|\).
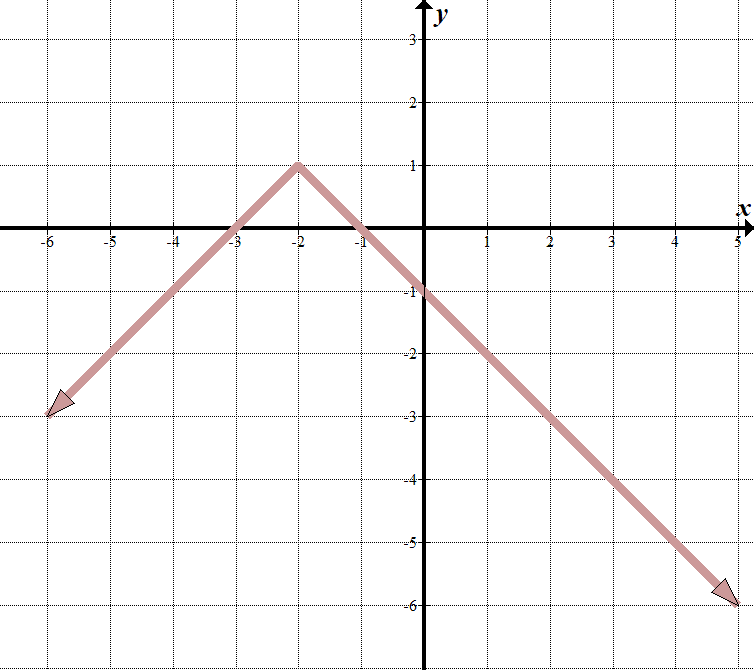	we zien dat onze” grenslijn ” op \(x=-2\) ligt, dus wat er in het absolute waardeteken zit moet \(x+2\) zijn. wanneer \(x>-2\), kunnen we zien dat de vergelijking van de lijn \(y=-x-1\) is. Wanneer \(x<-2\), is de regel \(y=x+3\). We kunnen dit schrijven als een stuksgewijze functie: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l} – x-1\,\,\,\,\,\,\tekst{if }x>-2\ \ x+3\,\,\,\,\,\,\,\,\,\,\tekst{if }x \ le -2 \ end{array} \ right.\) Het is waarschijnlijk makkelijker om dit als een getransformeerde absolute waarde functie te schrijven. We kunnen zien dat de bovenliggende absolute waarde functie verticaal wordt omgedraaid, naar links 2, en omhoog 1. Onze absolute waardevergelijking is \(y= – \ left / {x + 2} \ right|\,\,+\,\,1\). Dit is hetzelfde als de stuksgewijze functie hierboven. Probeer het – het werkt!

transformaties van stuksgewijze functies

laten we een transformatie van een stuksgewijze functie uitvoeren. We leerden hoe over Ouderfuncties en hun transformaties hier in de Oudergrafieken en transformaties sectie. U zult waarschijnlijk deze sectie eerst willen lezen, voordat u een stuksgewijze transformatie probeert.

laten we de volgende stuksgewijze functie omdraaien om de \(x\)-as, verticaal uitgerekt met een factor van 2 eenheden, 1 eenheid naar rechts, en 3 eenheden naar boven.

We zullen tekenen \(-2f\left( x-1 \right)+3\), waar:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\text{ als }x<&\text{ als 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ als }x\ge 4\end{align} \right.\)

laten we ervoor zorgen dat we de “grens” punten gebruiken wanneer we het T-diagram invullen voor de transformatie. Vergeet niet dat de transformaties binnen de haakjes worden gedaan naar de \(x\) (het doen van de tegenovergestelde wiskunde), en buiten worden gedaan naar de \(y\). Om te komen met een t-grafiek, zoals weergegeven in de tabel hieronder, kunnen we sleutelpunten gebruiken, waaronder twee punten op elk van de “grenslijnen”.

merk op dat omdat deze transformatie ingewikkeld is, we een nieuwe stuksgewijze functie kunnen bedenken door de 3 “stukken” te transformeren en ook de “\(x\)”S te transformeren waar de grenspunten zijn (1 optellen, of naar rechts 1 gaan), omdat we de tegenovergestelde wiskunde doen voor de “\(x\)”s. Om de nieuwe functies in elk interval te krijgen, kunnen we gewoon “\(x-1\)” vervangen door “\(x\)” in de oorspronkelijke vergelijking, vermenigvuldigen met -2, en dan 3 optellen. Bijvoorbeeld \(\displaystyle-2f \ left ({x-1} \right)+3=-2\left+3=-2\left ({x+3} \right)+3=-2x-3\).

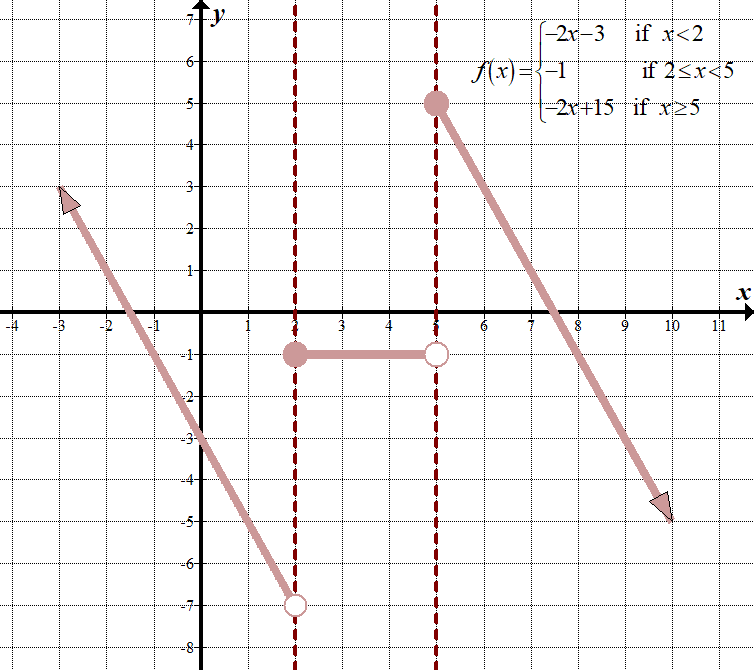
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2\left( {\left( {x-1} \right)+4} \right)+3=-2x-3,\,\,\,\,\text{ als }x-1<1\,\,\,\left( {x<2} \right)\\-2\left( 2 \right)+3=-1,\,\,\,\,\text{ als }\,\text{ 2 }\le x<5\\-2\left( {\left( {x-1} \right)-5} \right)+3=-2x+15,\,\,\,\,\text{ als }x\ge 5\end{array} \right.\)

Hier zijn de” voor “en” na ” grafieken, inclusief het T-diagram:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

uw favoriete hondenverzorgster rekent op basis van het gewicht van uw hond. Als uw hond is 15 pond en onder, de groomer kosten $ 35. Als uw hond tussen de 15 en 40 pond, ze rekent $ 40. Als uw hond is meer dan 40 pond, ze rekent $40, plus een extra $2 voor elk pond.

(a) Schrijf een stuksgewijze functie die beschrijft wat uw hond stalknecht opladt.

(B) Grafiek de functie.

(c) wat zou de groomer kosten als uw schattige hond 60 pond weegt?

oplossing:

(a) we zien dat de “grenspunten” 15 en 40 zijn, omdat dit de gewichten zijn waar de prijzen veranderen. Omdat we twee grenspunten hebben, hebben we drie vergelijkingen in onze stuksgewijze functie. We moeten beginnen bij 0, omdat honden meer dan 0 Pond moeten wegen:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{als }0<x\le 15\\\tekst{ }……\,\,\,\,\,\,\,\,\,\text{als }15<x\le 40\\\tekst{ }……\,\,\,\,\,\,\,\,\,\text{als }x>40\end{array} \right.\)

We zijn op zoek naar de” antwoorden “(hoeveel de verzorging kost) op de” vragen ” (hoeveel de hond weegt) voor de drie prijsklassen. De eerste twee zijn gewoon flat fees ($35 en $ 40, respectievelijk). De laatste vergelijking is wat lastiger; de groomer rekent $40 plus $2 voor elk pond boven de 40. Laten we eens echte nummers proberen: als uw hond 60 pond weegt, zal ze $40 plus $2 keer \(20(60-40)\) in rekening brengen. We zetten dit om in een vergelijking: \(40+2 (x–40)\), die vereenvoudigt tot \(2x-40\) (zie hoe 2 De Helling is?).

de gehele stuksgewijze functie is:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }0<x\le 15\\\tekst{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }15<x\le 40\\\text{ }40+2\left( {x-40} \right)\,\,\,\,\,\,\text{als }x>40\end{array} \right.\) of \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }0<x\le 15\\\tekst{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }15<x\le 40\\\text{ }2x-40\,\,\,\,\,\,\,\text{als }x>40\end{array} \right.\)

(b) laten we grafiek:merk op dat deze stuksgewijze vergelijking niet continu is. Merk ook op dat een redelijk domein voor dit probleem \(\left( {0,200} \right]\) kan zijn (gegeven honden wegen niet meer dan 200 pond!) en een redelijk bereik zou \(\left\cup \left\) kunnen zijn.

(c) als uw hond 60 pond weegt, kunnen we de grafiek of de functie gebruiken om te zien dat u $80 moet betalen. Whoa! Dat kost meer dan een menselijk kapsel (tenminste mijn kapsels)!

probleem:

U bent van plan om She Love Math T-shirts te verkopen als een fondsenwerver. De groothandel t-shirt bedrijf rekent u $ 10 per shirt voor de eerste 75 shirts. Na de eerste 75 shirts die u tot 150 shirts koopt, zal het bedrijf zijn prijs verlagen tot $ 7,50 per shirt. Na de aankoop van 150 shirts, zal de prijs dalen tot $ 5 per shirt. Schrijf een functie die deze situatie modelleert.

oplossing:

we zien dat de “grenspunten” 75 en 150 zijn, omdat dit het aantal gekochte T-shirts is waar de prijzen veranderen. Omdat we twee grenspunten hebben, hebben we drie vergelijkingen in onze stuksgewijze functie. We beginnen met \(x \ ge 1\), omdat we aannemen dat er tenminste één shirt is gekocht. Merk in dit probleem op dat het aantal gekochte T-shirts (\(x\)), of het domein, een geheel getal moet zijn, maar deze beperking mag de uitkomst van het probleem niet beïnvloeden.

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text{ if }1\le x\le 75\\\text {}….. \text {} 75<x\le 150\\\text {}…….. \Text{ if }x>150\end{array} \right.\)

We zijn op zoek naar de “antwoorden” (totale kosten van t-shirts) op de “vragen” (hoeveel worden er gekocht) voor de drie prijsklassen.

voor maximaal 75 shirts is de prijs $10, dus de totale prijs zou \(10x\). Voor meer dan 75 shirts maar tot 100 shirts, de kosten zijn $ 7.50 ,maar de eerste 75 t-shirts zal nog steeds kosten $10 per shirt. De tweede functie omvat de $ 750 besteed aan de eerste 75 shirts( 75 keer $ 10), en bevat ook $7.50 keer het aantal shirts boven de 75, wat \((x-75)\) zou zijn. Bijvoorbeeld, als je 80 shirts kocht, zou je \(\$10\keer 75=\$750\) moeten uitgeven, plus \(\$7.50\keer 5\,\) (80 – 75) voor de shirts na het 75ste shirt.

evenzo zouden we voor meer dan 150 overhemden nog steeds de $10 prijs omhoog betalen via 75 overhemden, de $7.50 prijs voor 76 tot 150 shirts (75 meer shirts), en dan $5 per shirt voor het aantal shirts gekocht meer dan 150. We betalen.\(10(75)+7.50(75)+5( x-150)\) voor \(x\) shirts. Zet in cijfers en probeer het!

De hele stuksgewijze functie is:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }1\le x\le 75\\\text{ }7,5 x\text{ }+\tekst{ }187.5\,\,\,\,\,\tekst{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if }x>150 \ end{array} \ right.\) of \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }1\le x\le 75\\\text{ }7,5 x\text{ }+\tekst{ }187.5\,\,\,\,\,\tekst{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{als }x>150\end{array} \right.\)

probleem:

een busdienst kost $ 50 voor de eerste 400 mijl, en elke extra 300 mijl (of een fractie daarvan) voegt $10 toe aan het tarief.

gebruik een stuksgewijze functie om het bustarief weer te geven in termen van de afstand in mijlen.

oplossing:

Dit is eigenlijk een lastig probleem, maar laten we eerst nadenken over het “grenspunt”, dat 400 is. Het is vrij eenvoudig als de rit minder dan 400 mijl is; de kosten zijn $ 50.

voor meer dan 400 mijl moeten we de eerste 400 mijl Aftrekken (maar vergeet niet de eerste $50 op te nemen), het aantal mijlen dat overblijft delen door 300 mijl (en naar boven afronden, als er een fractionele hoeveelheid is), en dat vermenigvuldigen met $10.

het lastige deel is wanneer we” round up ” voor een deel van de volgende 300 mijl. We kunnen een “plafond” functie gebruiken (aangeduid door \(\left \ lceil {} \ right \ rceil \)); deze functie geeft het kleinste geheel getal dat groter is dan of gelijk is aan zijn input; bijvoorbeeld, het plafond van zowel 3.5 als 4 is 4.

Dit is dus wat we hebben:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }50\tekst{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{als }0\le x\le 400\\\text{ }50+10\times \left\lceil {\frac{{x-400}}{{300}}} \rechts\rceil \tekst{ }\,\,\,\,\,\,\text{ als }x>400\end{array} \right.\)

laten we het proberen! Als we een 1500-mijl rijden, de kosten zou zijn \ (\displaystyle 50 + 10 \ times \ left \ lceil {\frac{{1500-400}}{{300}}} \rechts \ rceil \ text { } = 50+10 \ times 4 = \ $ 90\).

probleem:

welke waarde van \(\boldsymbol{a}\) zou deze stuksgewijze functie continu maken?

\(\displaystyle f \ left (x \ right)= \ left\ {\begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\tekst{ if }x<-2\ \ 5x+ \ boldsymbol{a}\,\,\,\,\,\,\,\,\text{if }x \ ge -2 \ end{array} \ right.\)

oplossing:

om de stuksgewijze functie continu te laten zijn, moeten op het grenspunt (waar de functie verandert) de twee \(y\) waarden hetzelfde zijn. We kunnen stekker in -2 voor \(x\) in beide functies en zorg ervoor dat de \(y\)’s zijn van dezelfde

\(\begin{align}3{{x}^{2}}+4&=5x+a\\3{{\left( {-2} \right)}^{2}}+4&=5\left( {-2} \right)+a\\12+4&=-10+a\\a&=26\end{align}\)

Als \(a=26\), de stuksgewijze functie is continu!

leer deze regels en oefen, oefen, oefen!

meer oefening: gebruik de Mathway widget hieronder om te proberen een stuksgewijze functie te schrijven. Klik op Submit (de blauwe pijl rechts van het probleem) en klik op Schrijf de Absolute waarde als stuksgewijs om het antwoord te zien.

u kunt ook uw eigen probleem typen, of klik op de drie puntjes in de rechterbovenhoek en klik op “Examples” om naar beneden te boren per onderwerp.

Als u op Tap klikt om stappen te bekijken, of hier klikt, kunt u zich bij Mathway registreren voor een gratis proefperiode en vervolgens upgraden naar een betaald abonnement op elk gewenst moment (om elk type wiskundeprobleem op te lossen!).

Op naar Matrices en het oplossen van systemen met Matrices – u bent klaar!