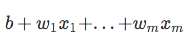een van de mooie eigenschappen van logistieke regressie is dat de sigmoid-functie de voorwaardelijke waarschijnlijkheden van de voorspelling, de klassenwaarschijnlijkheden, uitvoert. Hoe werkt het?Laten we beginnen met de zogenaamde “odds ratio” p / (1-p), die de verhouding beschrijft tussen de waarschijnlijkheid dat een bepaalde, positieve gebeurtenis plaatsvindt en de waarschijnlijkheid dat deze niet plaatsvindt – waarbij positief verwijst naar de “gebeurtenis die we willen voorspellen”, d.w.z., p(y=1 | x).
(merk op dat logistische regressie een speciaal soort sigmoid functie is, de logistische sigmoid; andere sigmoid functies bestaan bijvoorbeeld, de hyperbolische tangens).
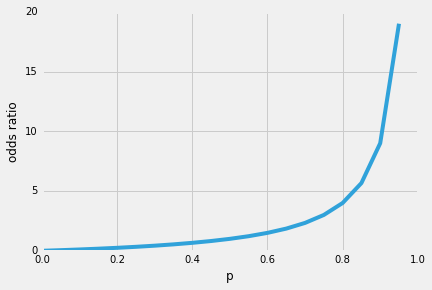
dus, hoe waarschijnlijker het is dat de positieve gebeurtenis optreedt, hoe groter de odds’ ratio.Nu, als we de natuurlijke logaritme van deze odds’ ratio, de log odds of logit-functie, krijgen we de volgende
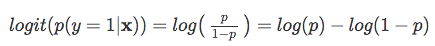
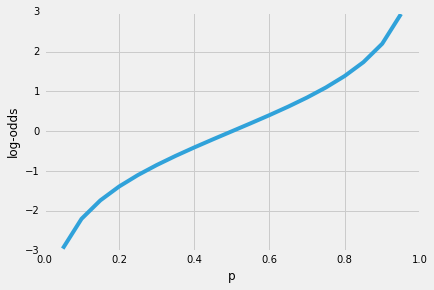
laten we nu gebruik maken van deze log-transformatie van het model de relatie tussen de verklarende variabelen en de variabele:
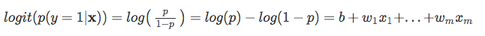
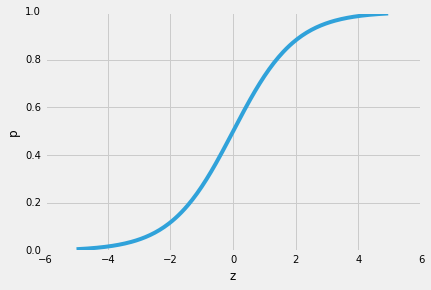
| Nu, onthoud het, dat we niet proberen te voorspellen van de juiste deel van de bovenstaande vergelijking, omdat *p(y=1 | x)* is wat we zijn echt geïnteresseerd in. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
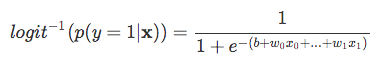
| which returns the class probabilities *p(y=1 | x)* from the inputs |