na het begrijpen van de exponentiële functie, is ons volgende doel de natuurlijke logaritme.

gegeven hoe de natuurlijke log wordt beschreven in wiskundeboeken, is er weinig “natuurlijk” over: het is gedefinieerd als de inverse van $e^x$, al een vreemde exponent genoeg.

maar er is een frisse, intuïtieve verklaring: de natuurlijke log geeft je de tijd die nodig is om een bepaald niveau van groei te bereiken.

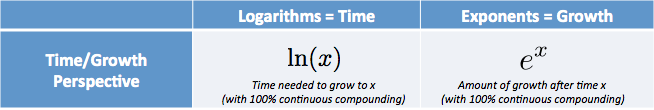
stel dat u een investering hebt in gummy bears (wie niet?) met een rente van 100% per jaar, die voortdurend groeit. Als je 10x groei wilt, uitgaande van continue compounding, zou je slechts $\ln(10)$ of 2.302 jaar wachten. Zie je niet waarom het slechts een paar jaar duurt om 10x groei te krijgen? Zie je niet waarom het patroon niet 1, 2, 4, 8 is? Lees meer over e.

e en de natuurlijke Log zijn tweelingen:

• $e^x$ is het bedrag dat we hebben na het starten bij 1.0 en continu groeien voor$ x $ tijdseenheden
• $ \ ln (x)$ (natuurlijke logaritme) is de tijd om $ x$ te bereiken, ervan uitgaande dat we continu groeiden van 1.0

niet al te slecht, toch? Terwijl de wiskundigen klauteren om u de lange, technische uitleg te geven, laten we duiken in de intuïtieve.

E gaat over groei

het getal e gaat over continue groei. Zoals we de vorige keer zagen, laat $E^X$ ons snelheid en tijd samenvoegen: 3 jaar bij 100% groei is hetzelfde als 1 jaar bij 300% groei, wanneer continu samengesteld.

We kunnen elke combinatie van tarief en tijd (50% voor 4 jaar) en converteren naar 100% voor het gemak (waardoor we 100% voor 2 jaar). Door te converteren naar een snelheid van 100% hoeven we alleen maar aan de tijdcomponent te denken:

intuïtief betekent $e^x$:

• hoeveel groei krijg ik na na X eenheden van tijd (en 100% continue groei)
• bijvoorbeeld: na 3 tijdsperioden heb ik $e^3$ = 20,08 keer de hoeveelheid “spul”.

$e^X$ is een schaalfactor, die ons laat zien hoeveel groei we zouden krijgen na $ x$ tijdseenheden.

natuurlijke Log is ongeveer tijd

het natuurlijke log is de inverse van $e^x$, een mooie term voor tegenovergestelde. Over Fantasie gesproken, de Latijnse naam is logaritmus naturali, wat de afkorting ln Geeft.

wat betekent dit inverse of tegengestelde materiaal?

• $e^x$ laat ons de tijd inpluggen en groei krijgen.
• $ \ ln (x)$ laat ons groei inpluggen en de tijd krijgen die het zou kosten.

bijvoorbeeld:

• $e^3$ is 20,08. Na 3 eenheden, eindigen we met 20.08 keer waarmee we begonnen.
• $ \ ln (20.08)$ is ongeveer 3. Als we groei van 20.08 willen, zouden we 3 eenheden van de tijd wachten (opnieuw, uitgaande van een 100% continue groei).

met mij? De natuurlijke log geeft ons de tijd die nodig is om onze gewenste groei te bereiken.

logaritmische rekenkunde is niet normaal

u hebt logboeken eerder bestudeerd en het waren vreemde beesten. Hoe hebben ze vermenigvuldiging omgezet in optellen? Delen in Aftrekken? Eens kijken.

Wat is $\ln (1)$? Intuïtief is de vraag: hoe lang wacht ik om 1x mijn huidige bedrag te krijgen?

nul. Zip. Nada. U bent al op 1x uw huidige bedrag! Het duurt niet lang om van 1 naar 1 te groeien.

• $\ln(1) = 0$

Ok, wat dacht je van een fractionele waarde? Hoe lang om 1/2 mijn huidige bedrag te krijgen? Ervan uitgaande dat je continu groeit met 100%, weten we dat $\ln(2)$ de hoeveelheid tijd is om te verdubbelen. Als we het omkeren (d.w.z. de negatieve tijd nemen) zouden we de helft van onze huidige waarde hebben.

• $ \ ln (.5) = – \ln(2)= -.693$

is logisch, toch? Als we achteruit gaan .693 eenheden (negatieve seconden, laten we zeggen) we zouden de helft van onze huidige hoeveelheid hebben. In het algemeen kun je de breuk omdraaien en het negatieve nemen: $\ln(1/3) = – \ln(3) = -1.09$. Dit betekent dat als we 1,09 tijdseenheden teruggaan, we een derde zouden hebben van wat we nu hebben.

Ok, hoe zit het met de natuurlijke log van een negatief getal? Hoeveel tijd kost het om je bacteriekolonie van 1 tot -3 te” laten groeien”?

Het is onmogelijk! Je kunt toch geen “negatieve” hoeveelheid bacteriën hebben? Op zijn hoogst (eh… minst) kun je nul hebben, maar er is geen manier om een negatieve hoeveelheid van de kleine beestjes te hebben. Negatieve bacteriën slaan nergens op.

• $\ln(\text{negatief getal}) = \text{undefined}$

Undefined betekent gewoon “er is geen tijd dat je kunt wachten” om een negatief bedrag te krijgen. (Nou, als we imaginaire exponentialen gebruiken, is er een oplossing. Maar laten we het vandaag echt houden.)

logaritmische vermenigvuldiging is erg leuk

Hoe lang duurt het om 9x je huidige hoeveelheid te laten groeien? Natuurlijk kunnen we gewoon ln(9) gebruiken. Maar dat is te makkelijk, laten we anders zijn.

We kunnen 9x groei beschouwen als verdrievoudiging (rekening houdend met $ \ ln (3)$ tijdseenheden) en dan weer verdrievoudiging (rekening houdend met een andere $ \ ln (3)$ tijdseenheden):

• tijd om te groeien 9x = $ \ ln (9)$ = tijd om te triple en triple opnieuw = $ \ ln (3) + \ ln (3) $

interessant. Elk groeigetal, zoals 20, kan worden beschouwd als 2x groei gevolgd door 10x groei. Of 4x groei gevolgd door 5x groei. Of 3x groei gevolgd door 6.666 x groei. Zie je het patroon?

• $\ln(a*b) = \ln(a) + \ln(b)$

de log van A keer b = log(a) + log(b). Deze relatie is zinvol als je denkt in termen van tijd om te groeien.

als we 30x willen groeien, kunnen we $\ln(30)$ in één keer wachten, of gewoon $\ln(3)$, om te verdrievoudigen, en dan $\ln(10)$, om weer 10x te groeien. Het netto effect is hetzelfde, dus de netto tijd moet hetzelfde zijn (en dat is het).

hoe zit het met delen? $ \ ln (5/3)$ betekent: hoe lang duurt het om 5 keer te groeien en dan 1/3 daarvan te nemen?

wel, 5 keer groeien is $\ln (5)$. Groei van 1/3 is $ – \ ln (3)$ tijdseenheden. Dus

• $\ln(5/3) = \ln(5) – \ln(3)$

wat zegt: groei 5 keer en “ga terug in de tijd” totdat je een derde van dat bedrag hebt, dus je blijft over met 5/3 groei. In het algemeen hebben we

• $\ln(a/b) = \ ln(a) – \ln (b)$

Ik hoop dat de vreemde wiskunde van logaritmen zin begint te krijgen: vermenigvuldiging van de groei wordt optellen van de tijd, verdeling van de groei wordt aftrekken van de tijd. Onthoud de regels niet, begrijp ze.

natuurlijke Logs gebruiken met een willekeurige snelheid

“zeker,” zeg je, ” dit logbestand werkt voor 100% groei, maar hoe zit het met de 5% die ik normaal krijg?”

Het is geen probleem. De ” tijd “die we terug krijgen van $\ln()$ is eigenlijk een combinatie van snelheid en tijd, de” x ” van onze $e^x$ vergelijking. We nemen 100% aan om het simpel te maken, maar we kunnen andere getallen gebruiken.

stel dat we 30x groei willen: plug $\ln(30)$ in en krijg 3.4. Dit betekent:

• $e^x = \ text{groei}$
• $e^{3.4} = 30$

en intuïtief betekent deze vergelijking “100% rendement voor 3,4 jaar is 30x groei”. We kunnen de vergelijking als volgt beschouwen:

We kan “Rate” en “time” wijzigen, zolang rate * time = 3.4. Bijvoorbeeld, stel dat we 30x groei willen-hoe lang wachten we ervan uitgaande dat 5% rendement?

• $\ln (30) = 3.4$
• $\text{rate} * \text{time} = 3.4$
• $.* \ Text{time} = 3.4$
• $ \ text{time} = 3.4 / .05 = 68 \ text{years}$

intuïtief denk ik dat ” $\ln(30) = 3,4$, dus bij 100% groei zal het 3,4 jaar duren. Als ik de groei verdubbel, halveer ik de benodigde tijd.”

• 100% gedurende 3,4 jaar = 1,0 * 3,4 = 3,4
• 200% gedurende 1,7 jaar = 2,0 * 1,7 = 3,4
• 50% gedurende 6,8 jaar = 0,5 * 6,8 = 3,4
• 5% gedurende 68 jaar=.05 * 68 = 3,4

Cool, eh? De natuurlijke log kan worden gebruikt met elke rente of tijd, zolang hun product hetzelfde is. Je kunt de variabelen wiebelen zoveel je wilt.

Awesome voorbeeld: de regel van 72

De regel van 72 is een mentale wiskundige snelkoppeling om de tijd in te schatten die nodig is om uw geld te verdubbelen. We gaan het afleiden (yay!) en nog beter, we gaan het intuïtief begrijpen.

hoe lang duurt het om uw geld te verdubbelen tegen 100% rente, elk jaar verhoogd?

Uh oh. We gebruiken natuurlijke log voor continue tarieven, maar nu vraag je om jaarlijkse rente? Zal dit onze formule niet verpesten? Ja, dat zal het, maar bij een redelijke rente zoals 5%, 6% of zelfs 15%, is er niet veel verschil tussen jaarlijkse samengestelde en volcontinue rente. Dus de ruwe formule werkt ruwweg en we doen alsof we continu interesse krijgen.

nu is de vraag eenvoudig: hoe lang te verdubbelen met 100% rente? ln (2)=.693. Het duurt .693 eenheden van de tijd (jaar, in dit geval) om uw geld te verdubbelen met continue compounding met een tarief van 100%.

Ok, wat als onze rente niet 100% is wat als het 5% of 10% is?

eenvoudig. Zolang tarief * tijd=.693, we zullen ons geld verdubbelen:

• rate * time=.693
• time = .693 / rate

dus, als we slechts 10% groei, het zou nemen .693 / .10 of 6,93 jaar tot het dubbele.

om dingen te vereenvoudigen, laten we vermenigvuldigen met 100 zodat we kunnen praten over 10 in plaats van .10:

• tijd tot double = 69,3 / rate, waarbij rate wordt verondersteld in procenten te zijn.

nu is de tijd om met een groei van 5% te verdubbelen 69,3 / 5 of 13,86 jaar. 69.3 is echter niet het meest Deelbare getal. Laten we een naaste buurman kiezen, 72, die gedeeld kan worden door 2, 3, 4, 6, 8 en nog veel meer getallen.

• time to double = 72 / rate

dat is de regel van 72! Rustig aan.

als je de tijd wilt vinden om te verdrievoudigen, gebruik je ln(3) ~ 109.8 en krijg je

• tijd tot verdrievoudiging = 110 / rate

wat een andere nuttige vuistregel is. De regel van 72 is nuttig voor rente, Bevolkingsgroei, bacterieculturen en alles wat exponentieel groeit.

waarheen vanaf hier?

Ik hoop dat de natuurlijke log meer zin heeft — het vertelt je de tijd die nodig is voor elke hoeveelheid exponentiële groei. Ik beschouw het als” natuurlijk “omdat e de universele groeisnelheid is, dus ln kan beschouwd worden als de” universele ” manier om erachter te komen hoe lang het duurt om te groeien.

als je $\ln(x)$ ziet, denk dan gewoon aan “de hoeveelheid tijd om naar x te groeien”. In het volgende artikel brengen we e en ln samen, en de zoete geur van wiskunde zal de lucht vullen.

Appendix: de natuurlijke Log van E

Quick quiz: Wat is $ \ ln (e)$?

• De wiskundige robot zegt: omdat ze zijn gedefinieerd als inverse functies, is duidelijk $ \ ln ( e) = 1$
• de intuïtieve mens: ln(e) is de hoeveelheid tijd die nodig is om “e” eenheden van groei te krijgen (ongeveer 2.718). Maar e is de hoeveelheid groei na 1 tijdseenheid, dus $ \ ln ( e) = 1$.

denk intuïtief.

andere posten in deze serie

1. Een intuïtieve Gids Voor exponentiële functies & e
2. Demystifying The Natural logaritme (ln)
3. een visuele gids voor eenvoudige, samengestelde en continue rente
4. gemeenschappelijke definities van e (gekleurd)
5. exponenten begrijpen (waarom doet 0^0 = 1?)
6. logaritmen gebruiken in de echte wereld
7. Hoe te denken met exponenten en Logaritmen
8. Discrete Versus continue groei
9. Wat betekent een exponent werkelijk?
10. Q: Waarom is e speciaal? (2.718… niet 2, 3,7 of een ander getal?)