Les 3: complexe formules
/en/excelfulas/simple-formulas/content/
Inleiding
een eenvoudige formule is een wiskundige uitdrukking met één operator, zoals 7+9. Een complexe formule heeft meer dan één wiskundige operator, zoals 5+2*8. Wanneer er meer dan één bewerking in een formule is, vertelt de volgorde van bewerkingen aan uw spreadsheet welke bewerking het eerst moet worden berekend. Om complexe formules te gebruiken, moet u de volgorde van bewerkingen begrijpen.
facultatief: Download ons voorbeeldbestand voor deze les.
bekijk de video hieronder voor meer informatie over complexe formules.
De volgorde van handelingen.
Alle spreadsheet-programma ‘ s berekenen met formules gebaseerd op de volgende volgorde van bewerkingen:
- Bewerkingen tussen haakjes
- Exponentiële berekeningen (3^2 bijvoorbeeld)
- Vermenigvuldigen en delen, wat het eerst komt
- Optellen en aftrekken, wat het eerst komt
Een ezelsbruggetje die u kunnen helpen onthoud de volgorde is PEMDAS, of Gelieve Excuus Mijn Lieve Tante Sally.
klik op de pijlen in de diavoorstelling hieronder voor meer informatie over hoe de volgorde van bewerkingen wordt gebruikt om complexe formules te berekenen.
-

hoewel deze formule er heel ingewikkeld uit kan zien, kunnen we de volgorde van bewerkingen stap voor stap gebruiken om het juiste antwoord te vinden.
-

eerst zullen we beginnen met het berekenen van iets tussen de haakjes. In dit geval is er maar één ding dat we moeten berekenen: 6-3=3.
-

zoals u kunt zien, ziet de formule er al een beetje eenvoudiger uit. Vervolgens kijken we of er exponenten zijn. Er is één: 2^2 = 4.
-

vervolgens lossen we elke vermenigvuldiging en deling op, werkend van links naar rechts. Omdat de delingsoperatie voor de vermenigvuldiging komt, wordt deze eerst berekend: 3/4 = 0,75.
-

nu berekenen we onze resterende vermenigvuldigingsoperatie: 0,75*4=3.
-

vervolgens berekenen we elke optelling of aftrekking, opnieuw werkend van links naar rechts. Optellen komt eerst: 10 + 3 = 13.
-

tenslotte hebben we nog één aftrekking: 13-1=12.
-

en nu hebben we ons antwoord: 12. Dit is precies hetzelfde resultaat dat je zou krijgen als je de formule in een spreadsheet ingevoerd.

het gebruik van haakjes binnen een formule kan erg belangrijk zijn. Vanwege de volgorde van de operaties, kan het een antwoord volledig veranderen. Laten we hetzelfde probleem van boven proberen, maar deze keer voegen we haakjes toe aan het laatste deel.
complexe formules aanmaken
in het voorbeeld hieronder zullen we een complexe formule demonstreren met behulp van de volgorde van bewerkingen. Hier willen we de kosten van de omzetbelasting berekenen voor een catering factuur. Om dit te doen, schrijven we onze formule als =(D2+D3)*0.075 in cel D4. Deze formule voegt de prijzen van onze items bij elkaar en vermenigvuldigt die waarde met de 7,5% belastingtarief (dat is geschreven als 0,075) om de kosten van omzetbelasting te berekenen.
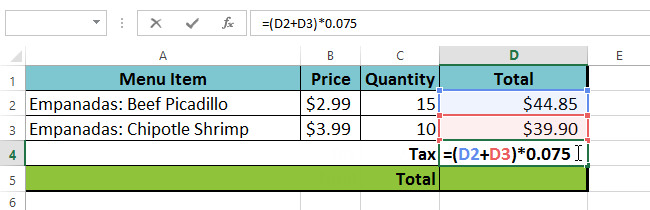
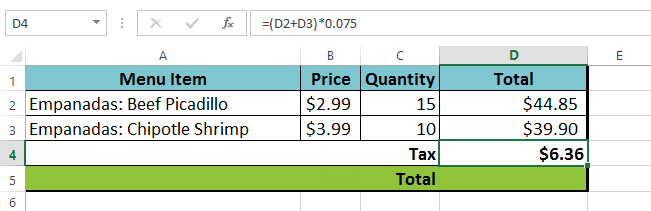
Het spreadsheet volgt dan de volgorde van bewerkingen en voegt eerst de waarden tussen de haakjes toe: (44.85+39.90) = $84.75. Dan vermenigvuldigt het die waarde met het belastingtarief: $ 84.75 * 0.075. Het resultaat zal laten zien dat de omzetbelasting is $ 6.36.
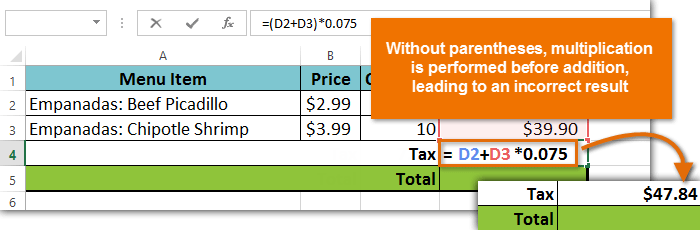
Het is vooral belangrijk om complexe formules in te voeren met de juiste volgorde van bewerkingen. Anders zal de spreadsheet de resultaten niet nauwkeurig berekenen. In ons voorbeeld, als de haakjes niet zijn opgenomen, wordt de vermenigvuldiging eerst berekend en is het resultaat onjuist. Haakjes zijn de beste manier om te bepalen welke berekeningen eerst in een formule worden uitgevoerd.
om een complexe formule te maken met behulp van de volgorde van bewerkingen:
in ons voorbeeld hieronder gebruiken we celverwijzingen samen met numerieke waarden om een complexe formule te maken die de totale kosten voor een catering factuur berekent. De formule berekent de kosten voor elk menu-item en voegt deze waarden samen.
- Selecteer de cel die de formule zal bevatten. In ons voorbeeld selecteren we cel C4.
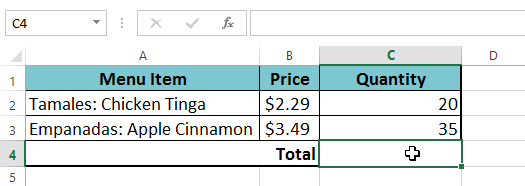
- Voer uw formule in. In ons voorbeeld typen we = B2 * C2+B3 * C3. Deze formule volgt de volgorde van bewerkingen en voert eerst vermenigvuldiging uit: 2,29 * 20 = 45,80 en 3,49 * 35 = 122,15. Vervolgens worden deze waarden bij elkaar opgeteld om het totaal te berekenen: 45.80+122.15.
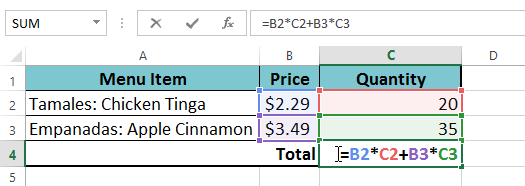
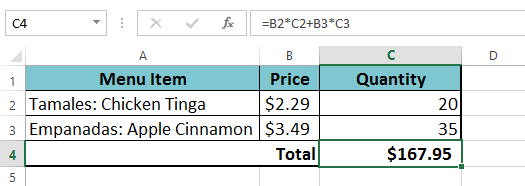
- controleer uw formule op nauwkeurigheid en druk vervolgens op Enter op uw toetsenbord. De formule berekent en toont het resultaat. In ons voorbeeld laat het resultaat zien dat de totale kosten voor de bestelling $167,95 zijn.
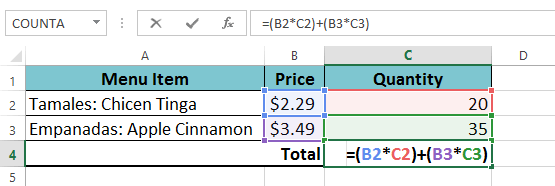
U kunt haakjes toevoegen aan elke vergelijking om het lezen te vergemakkelijken. Hoewel het het resultaat van de formule in dit voorbeeld niet zal veranderen, kunnen we de vermenigvuldigingsoperaties tussen haakjes om te verduidelijken dat ze vóór de optelling zullen worden berekend.
uw spreadsheet zal u niet altijd vertellen of uw Formule Een fout bevat, dus het is aan u om al uw formules te controleren. Om te leren hoe u dit moet doen, kijk dan op de les dubbel-controleer uw formules.
uitdaging!
- Open een bestaande Excel-werkmap. Als je wilt, kun je het voorbeeldbestand gebruiken voor deze les.
- Maak een complexe formule die optellen voor vermenigvuldiging zal uitvoeren. Als u het voorbeeld gebruikt, maakt u een formule in cel D6 die eerst de waarden van cellen D3, D4 en D5 toevoegt en vervolgens hun totaal vermenigvuldigt met 0,075. Hint: Je moet nadenken over de volgorde van bewerkingen om dit correct te laten werken.