In andere secties werd vermeld dat veel van de eigenschappen van vaste stoffen, vloeistoffen en gassen kunnen worden verklaard als we aannemen dat stoffen zijn gemaakt van atomen of moleculen die constant in beweging zijn. De wet van Boyle en de andere gaswetten hebben ons nu veel meer kwantitatieve informatie over gassen gegeven, en het is de moeite waard de vraag te stellen of we met het vorige model kwantitatieve voorspellingen kunnen doen in overeenstemming met deze wetten. Bij het beantwoorden van deze vraag krijgen we ook belangrijke inzichten in de aard van temperatuur en warmte-energie.

de microscopische theorie van gasgedrag gebaseerd op moleculaire beweging wordt de kinetische theorie van gassen genoemd. De basispostulaten zijn vermeld in Tabel 1:

TABLE \(\Paginindex{1}\) postulaten van de kinetische theorie van gassen.

1 de moleculen in een gas zijn klein en zeer ver van elkaar verwijderd. Het grootste deel van het volume dat een gas inneemt is lege ruimte.

2 gasmoleculen zijn in constante willekeurige beweging. Net zo veel moleculen bewegen in de ene richting als in elke andere.

3 moleculen kunnen met elkaar en met de wanden van de container botsen. Botsingen met de wanden zijn verantwoordelijk voor de druk van het gas.

4 bij botsingen verliezen de moleculen geen kinetische energie, dat wil zeggen dat de botsingen volkomen elastisch zijn. De totale kinetische energie van alle moleculen blijft constant, tenzij er enige externe interferentie is met de

5 de moleculen oefenen geen aantrekkelijke of afstotende krachten op elkaar uit, behalve tijdens het botsproces. Tussen botsingen bewegen ze in rechte lijnen.

daaruit kan de volgende uitdrukking voor de druk van een gas worden afgeleid in termen van de eigenschappen van zijn moleculen:

\ waarbij P, V = druk en volume van het gas

N = aantal moleculen

m = massa van elk molecuul

(u2)ave = gemiddelde (of gemiddelde) van de kwadraten van alle individuele moleculaire snelheden. Deze gemiddelde vierkante snelheid moet worden gebruikt omdat de druk evenredig is met het kwadraat van de moleculaire snelheid, en moleculaire botsingen veroorzaken dat verschillende moleculen heel verschillende snelheden hebben.

in plaats van ons bezig te houden met de procedure voor het afleiden van Eq. \(\ref{1}\), Laten we de vergelijking inspecteren en zien dat de Algemene kenmerken zijn zoals we zouden verwachten. In sommige opzichten is de mogelijkheid om dit te doen met een formule nuttiger dan de mogelijkheid om het af te leiden. Figuur \(\Paginindex{1}\)

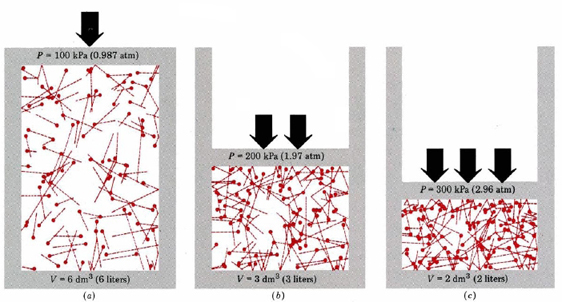allereerst vertelt de vergelijking ons dat de druk van een gas evenredig is met het aantal moleculen gedeeld door het volume. Dit wordt grafisch weergegeven in Figuur \(\Paginindex{1}\), waar een computer hetzelfde aantal gasmoleculen heeft getekend die elk van drie verschillende volumes bezetten. De “staart” op elke molecule toont de exacte weg gevolgd door die molecule in de vorige microseconde—hoe langer de staart, hoe sneller de molecule ging. Het gemiddelde van de vierkanten van de staartlengtes is evenredig met (u2)ave en is hetzelfde in alle drie de diagrammen. Er wordt ook aangenomen dat alle moleculen gelijke massa ‘ s hebben.

zoals u kunt zien, verhoogt het verminderen van het volume van het gas het aantal botsingen per oppervlakte-eenheid op de wanden van de tank. Elke botsing oefent kracht uit op de muur; kracht per oppervlakte-eenheid is druk, en dus is het aantal botsingen per oppervlakte-eenheid evenredig met de druk. Halvering van het volume verdubbelt de druk, een voorspelling die overeenkomt met de experimentele feiten samengevat in de wet van Boyle. Vergelijking \(\ref{1}\) zegt ook dat de druk evenredig is met de massa van elk gasmolecuul. Nogmaals, dit is wat we zouden verwachten. Zware moleculen geven een grotere “duw”(de technische term hiervoor is impuls) tegen de muur dan lichte met dezelfde snelheid.

tenslotte vertelt de vergelijking ons dat de druk evenredig is met het gemiddelde van de kwadraten van de moleculaire snelheden. Deze afhankelijkheid van het kwadraat van de snelheid is redelijk als we ons realiseren dat verdubbeling van de snelheid van een molecuul twee effecten heeft.

ten eerste kan het molecuul in een bepaalde tijd verder bewegen, waarbij het aantal botsingen met de wanden verdubbeld wordt. Dit zou de druk verdubbelen. Ten tweede, het verdubbelen van de snelheid van een molecuul verdubbelt de duw of impuls van elke botsing. Dit verdubbelt de druk weer. Daarom verdubbelt het verdubbelen van de snelheid van een molecuul de druk, en voor een groot aantal molecules, is P evenredig aan de gemiddelde vierkante snelheid.