Boyle ‘ s Law
Robert Boyle (1627-1691), een Engels chemicus, wordt algemeen beschouwd als een van de grondleggers van de moderne experimentele wetenschap van de chemie. Hij ontdekte dat een verdubbeling van de druk van een ingesloten gasmonster met behoud van de temperatuur constant het volume van het gas met de helft verminderde. De wet van Boyle stelt dat het volume van een bepaalde gasmassa omgekeerd varieert met de druk wanneer de temperatuur constant wordt gehouden. Een omgekeerde relatie wordt op deze manier beschreven. Naarmate de ene variabele in waarde toeneemt, neemt de andere af.
fysiek, wat gebeurt er? De gasmoleculen bewegen en bevinden zich op een bepaalde afstand van elkaar. Een toename van de druk duwt de moleculen dichter bij elkaar, waardoor het volume. Als de druk wordt verlaagd, zijn de gassen vrij om in een groter volume te bewegen.

wiskundig kan de wet van Boyle worden uitgedrukt met de vergelijking:
\
De \(k\) is een constante voor een bepaald gasmonster en hangt alleen af van de massa van het gas en de temperatuur. De onderstaande tabel toont druk – en volumegegevens voor een bepaalde hoeveelheid gas bij een constante temperatuur. De derde kolom vertegenwoordigt de waarde van de constante \(\left (k \right)\) voor deze gegevens en is altijd gelijk aan de druk vermenigvuldigd met het volume. Als een van de variabelen verandert, verandert de andere zodanig dat het product van \(P \maal V\) altijd hetzelfde blijft. In dit specifieke geval is die constante \(500\: \text{atm}\cdot \ text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
een grafiek van de gegevens in de tabel illustreert verder het omgekeerde relatiekarakter van de wet van Boyle (zie onderstaande figuur). Volume wordt uitgezet op de \(x\)-as, met de bijbehorende druk op de \(y\)-as.
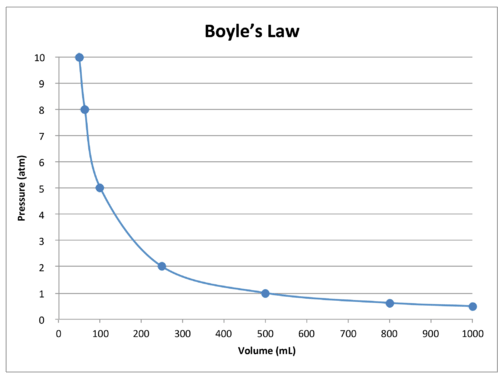
De Wet van Boyle kan worden gebruikt om veranderende omstandigheden voor een gas te vergelijken. We gebruiken \(P_1\) en \(V_1\) om voor de begindruk en het beginvolume van een gas te staan. Na een wijziging staan \(P_2\) en \(V_2\) voor de uiteindelijke druk en het volume. De wiskundige relatie van Boyle ‘ s wet wordt:
\
deze vergelijking kan worden gebruikt om een van de vier grootheden te berekenen als de andere drie bekend zijn.
voorbeeld \(\Paginindex{1}\)
een monster van zuurstofgas heeft een volume van \(425 \: \text{mL}\) wanneer de druk gelijk is aan \(387 \: \text{kPa}\). Het gas mag uitzetten in een \ (1.75\:\ text{L}\) container. Bereken de nieuwe druk van het gas.
oplossing
Stap 1: som de bekende hoeveelheden op en plan het probleem.
bekend
- \(P_1 = 387 \:\text{kPa}\)
- \ (V_1 = 425\:\text{mL}\)
- \ (V_2 = 1,75\: \ text{L} = 1750\:\text{mL}\)
onbekend
- \ (P_2 = ? \ : \ text{kPa}\)
gebruik de wet van Boyle om de onbekende druk \(\left( P_2 \right)\) op te lossen. Het is belangrijk dat de twee volumes (\(V_1\) en \(V_2\)) in dezelfde eenheden worden uitgedrukt, dus \(V_2\) is geconverteerd naar \(\text{mL}\).
Stap 2: oplossen.
eerst, herschik de vergelijking algebraïsch om op te lossen voor \(P_2\).
\
vervang nu de bekende hoeveelheden in de vergelijking en los op.
\
stap 3: Denk na over uw resultaat.
het volume is toegenomen tot iets meer dan 4 keer de oorspronkelijke waarde en dus is de druk met ongeveer een vierde afgenomen. De druk staat in \(\text{kPa}\) en de waarde heeft drie significante cijfers. Merk op dat elke druk-of volume-eenheden kunnen worden gebruikt, zolang ze consistent zijn gedurende het hele probleem.