Boyles Lov
Robert Boyle (1627-1691), en engelsk kjemiker, er allment ansett for å være en av grunnleggerne av den moderne eksperimentelle vitenskapen om kjemi. Han oppdaget at dobling av trykket i en lukket prøve av gass mens temperaturen var konstant, førte til at volumet av gassen ble redusert med halvparten. Boyles lov sier at volumet av en gitt masse gass varierer omvendt med trykket når temperaturen holdes konstant. Et omvendt forhold er beskrevet på denne måten. Når en variabel øker i verdi, reduseres den andre variabelen.
Fysisk, Hva skjer? Gassmolekylene beveger seg og er en viss avstand fra hverandre. En økning i trykk skyver molekylene nærmere sammen, og reduserer volumet. Hvis trykket reduseres, er gassene fri til å bevege seg i et større volum.

Matematisk Kan Boyles lov uttrykkes av ligningen:
\
\(k\) er en konstant for en gitt prøve av gass og avhenger bare av gassens masse og temperaturen. Tabellen nedenfor viser trykk – og volumdata for en bestemt mengde gass ved konstant temperatur. Den tredje kolonnen representerer verdien av konstanten \(\venstre (k \ høyre)\) for disse dataene og er alltid lik trykket multiplisert med volumet. Når en av variablene endres, endres den andre på en slik måte at produktet av \(p \ganger V\) alltid forblir det samme. I dette spesielle tilfellet er den konstanten \(500\: \ text{atm} \cdot \ text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
en graf av dataene i tabellen videre illustrerer boyles lovs inverse forhold (se figur nedenfor). Volum er plottet på \(x\)-aksen, med det tilsvarende trykket på \(y\)-aksen.
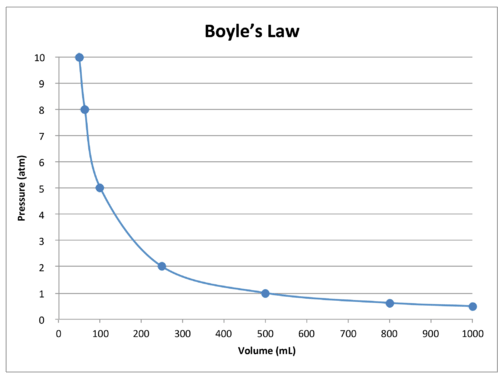
Boyles Lov kan brukes til å sammenligne endrede forhold for en gass. Vi bruker \(P_1\) og \(V_1\) for å stå for det første trykket og det første volumet av en gass. Etter at en endring er gjort, \(P_2\) og \(V_2\) står for det endelige trykket og volumet. Det matematiske forholdet Til Boyles Lov blir:
\
denne ligningen kan brukes til å beregne en av de fire mengdene hvis de andre tre er kjent.
Eksempel \(\PageIndex{1}\)
en prøve av oksygengass har et volum på \(425 \: \text{mL}\) når trykket er lik \(387 \: \ text{kPa}\). Gassen får lov til å ekspandere til en \ (1,75\:\ text{L}\) beholder. Beregn det nye trykket på gassen.
Løsning
Trinn 1: Oppgi kjente mengder og planlegg problemet.
Kjent
- \(P_1 = 387 \: \tekst{kPa}\)
- \(V_1 = 425 \: \tekst{mL}\)
- \(V_2 = 1,75 \: \tekst{L} = 1750 \: \tekst{mL}\)
Ukjent
- \(p_2= ? \: \ text{kPa}\)
Bruk Boyles Lov til å løse for det ukjente trykket \(\venstre (P_2 \ høyre)\). Det er viktig at de to volumene (\(V_1\) og \(V_2\)) uttrykkes i de samme enhetene, så \(V_2\) er konvertert til \(\text{mL}\).
Trinn 2: Løs.
først må du omorganisere ligningen algebraisk for å løse for \(P_2\).
\
erstatt nå de kjente mengdene i ligningen og løs.
\
Trinn 3: Tenk på resultatet ditt.
volumet har økt til litt over 4 ganger sin opprinnelige verdi, og så reduseres trykket med om lag en fjerdedel. Trykket er i \(\text{kPa}\) og verdien har tre signifikante tall. Merk at alle trykk-eller volumenheter kan brukes så lenge de er konsistente gjennom hele problemet.