Atomic Orbitals
en orbital er kvantemekanisk foredling Av Bohrs bane. I motsetning til hans konsept om en enkel sirkulær bane med en fast radius, er orbitaler matematisk avledede romområder med forskjellige sannsynligheter for å ha et elektron.
En måte å representere elektron sannsynlighetsfordelinger ble illustrert I Figur 6.5.2 for 1s orbital av hydrogen. Fordi Ψ 2 gir sannsynligheten for å finne et elektron i et gitt volum av plass (for eksempel et kubisk picometer), er et plott Av Ψ 2 versus avstand fra kjernen (r) et plott av sannsynlighetstettheten. 1s-orbitalet er sfærisk symmetrisk, så sannsynligheten for å finne en 1s-elektron på et gitt punkt avhenger bare av avstanden fra kjernen. Sannsynlighetstettheten er størst ved r = 0 (ved kjernen) og avtar jevnt med økende avstand. Ved svært store verdier av r er elektronens sannsynlighetstetthet svært liten, men ikke null.i motsetning kan vi beregne den radiale sannsynligheten (sannsynligheten for å finne en 1s elektron i en avstand r fra kjernen) ved å legge sammen sannsynlighetene for at et elektron er på alle punkter på en serie x sfæriske skall med radius r1, r2, r3,…, rx − 1, rx. I virkeligheten deler vi atomet i meget tynne konsentriske skall, akkurat som lagene av en løk (del (a) I Figur \(\PageIndex{1}\)), og beregner sannsynligheten for å finne et elektron på hvert sfærisk skall. Husk at elektronens sannsynlighetstetthet er størst ved r = 0 (del (b) I Figur \(\PageIndex{1}\)), så tettheten av prikker er størst for de minste sfæriske skallene i del (a) I Figur \(\PageIndex{1}\). I kontrast er overflaten av hvert sfærisk skall lik 4nr2, noe som øker veldig raskt med økende r (del (c) I Figur \(\PageIndex{1}\)). Fordi overflatearealet til de sfæriske skallene øker raskere med økende r enn elektron-sannsynlighetstettheten minker, har plottet av radial sannsynlighet et maksimum på en bestemt avstand (del (d) I Figur \(\PageIndex{1}\)). Viktigst, når r er svært liten, er overflaten av et sfærisk skall så lite at den totale sannsynligheten for å finne et elektron nær kjernen er svært lav; ved kjernen forsvinner elektronens sannsynlighet (del (d) I Figur \(\PageIndex{1}\)).

for hydrogenatomet oppstår toppen i radial sannsynlighetsplott ved r = 0.529 Å (52.9 pm), som er nøyaktig radiusen beregnet Av Bohr for n = 1 bane. Dermed er den mest sannsynlige radiusen oppnådd fra kvantemekanikk identisk med radiusen beregnet av klassisk mekanikk. I Bohrs modell ble imidlertid elektronen antatt å være på denne avstanden 100% av tiden, mens i den kvantemekaniske Schrö-modellen er det bare på denne avstanden en del av tiden. Forskjellen mellom de to modellene skyldes elektronens bølgelignende oppførsel og heisenbergs usikkerhetsprinsipp.
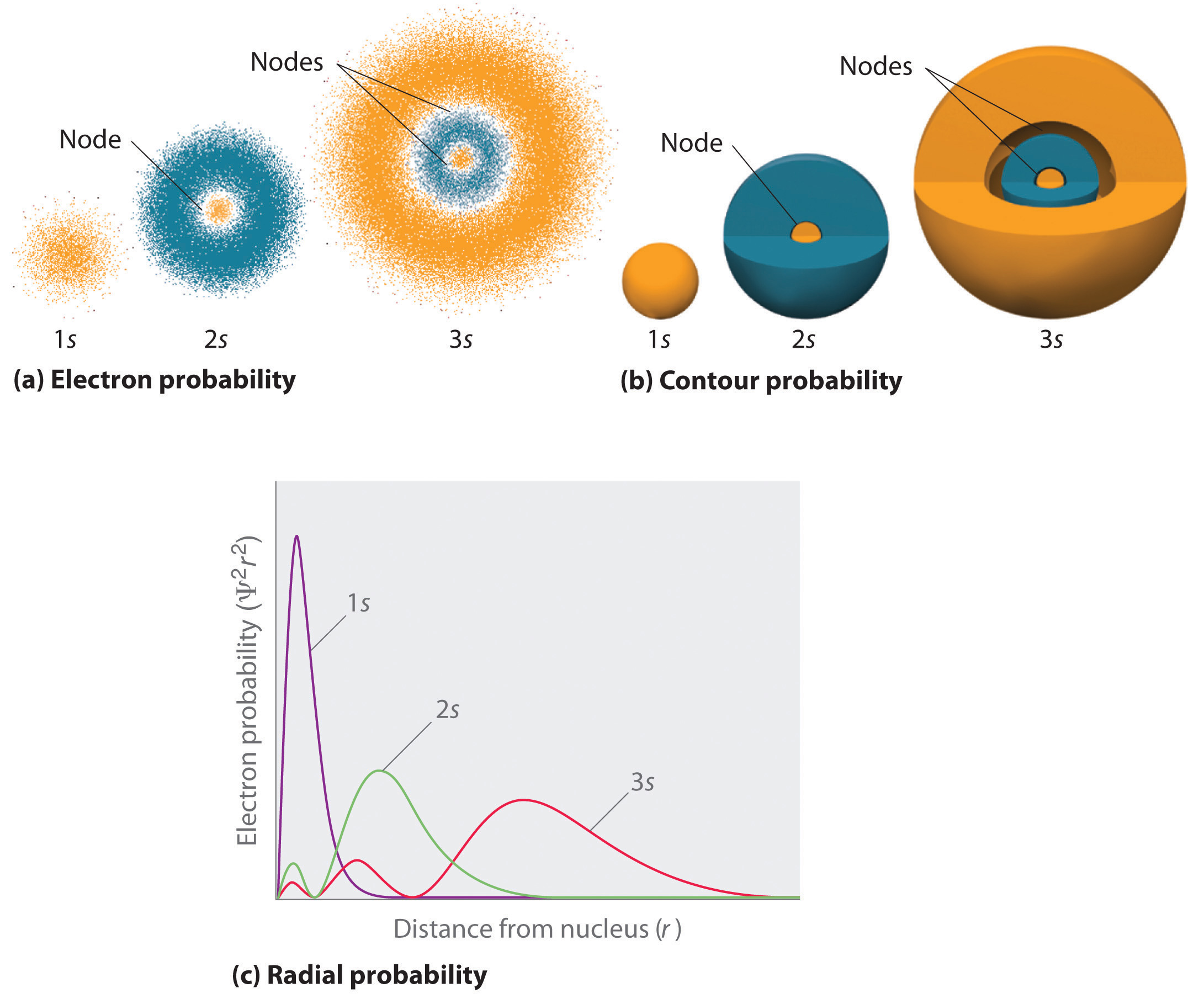
Figur \(\PageIndex{2}\) sammenligner elektronens sannsynlighetstettheter for hydrogen 1s, 2s og 3s orbitaler. Merk at alle tre er sfærisk symmetriske. For 2s og 3s orbitaler, men (og for alle andre s orbitaler også), faller elektronsannsynlighetstettheten ikke jevnt med økende r. I Stedet observeres en serie minima og maxima i de radiale sannsynlighetsplottene (del (c) I Figur \(\PageIndex{2}\)). Minima tilsvarer sfæriske noder (regioner med null elektron sannsynlighet), som veksler med sfæriske regioner med ikke-null elektron sannsynlighet.