각도와 원에 대한 몇 가지 흥미로운 것들.
새겨진 각
첫 번째 정의
새겨진 각도:는 각도에서 만든 점에 앉아있는 원형의 둘레를 표시합니다.
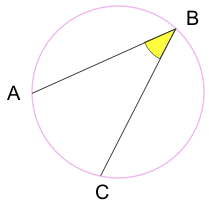
C 는”끝 지점”
B”apex point”
플레이 그것으로 여기:
이동할 때는 지점”B”,무엇이 일어나는 각?
새겨진 각 Theorems
새겨진각°은 절반의 각도를 중앙 2a°
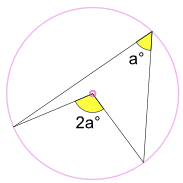
(이라는 각도에서 센터 정리)
고(을 유지 엔드 포인트 고정)… … 각도는°은 항상
상관없이 그것에 동의 끝에 포함되지 않았습니다.
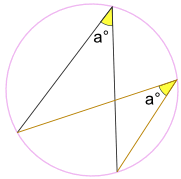
각도는°은 동일합니다.
(동일한 아크 정리에 의해 Subtended 각도라고 함)
예:각도 POQ 의 크기는 얼마입니까? (O 은 원형의 중앙)
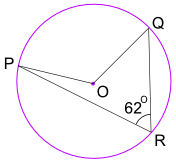
각 개의 poq=2×각 PRQ= 2 × 62° = 124°
예:크기는 무엇입의 각 CBX?
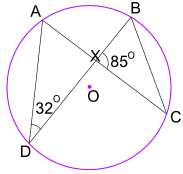
각도 ADB=32°또한 각도 ACB 와 같습니다.
및 각도 ACB 도 각도 XCB 와 같습니다.
그래서 삼각형 bxc 에서 우리는 각도 bxc=85°를 알고 있으며 각도 XCB=32°
이제 삼각형의 각도를 180°에 추가하십시오 :
각도에서 반원(탈레스의 정리)
각도 새겨져에서 원의 직경 권리는 항상각:
(엔드 포인트 중 하나 끝 원형 직경의,
에이펙스 시점에 할 수 있습립니다. 나는 이것이 내가 할 수있는 유일한 방법이라고 생각한다. 왜냐하면:
새겨진 각 90°은 절반의 중앙 각 180°
(“를 사용하여 각도를 중앙에 정리”위)
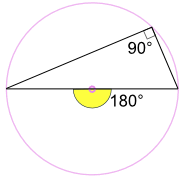
또 다른 좋은 이유가 왜 그것은 작품
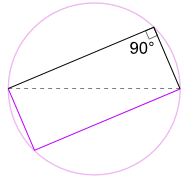
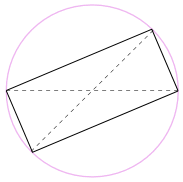
우리는 또한 회전,모 180°사각형을 만들기 위해!왜냐하면 모든면이 평행하고 두 대각선이 동일하기 때문입니다.
따라서 내부 각도는 모두 직각(90°)입니다.
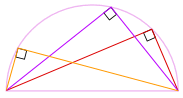
그래서 우리는 간다! 그 각도가 원주에서
인 위치에 상관없이 항상 90°
예:각도 BAC 의 크기는 얼마입니까?
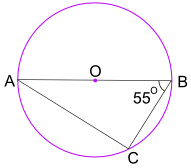
각도에서 반 정리고 우리에게 각 ACB=90°
지금 사용하여 삼각형의 각도 추가 180°을 찾아 각 BAC:
을 찾은 원형의 중심
우리가 사용할 수 있습니다 이런 생각을 동의 센터
- 그리도는 어디에서든 원의 원주를 그릴 직경을 어디에 두 다리를 명중 원
- 는 하지만 다른 직경
어디에 직경이 십자가를 중심!
주기적인 사각형
|
A”주기”사각형은 모든 꼭지점에의 원둘레: |
 |
|
주기적인 사각형의 반대 각도 추가 180°:
|
 |
를 들어: 의 크기는 무엇입 각 WXY?
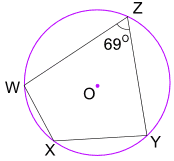
Opposite angles of a cyclic quadrilateral add to 180°

