이 섹션에서는 다룹니다:

• 소개 구분 함수
• 평가를 구분 함수
• 구분 함수의 그래프
• 는 방법을 말하면 구분의 기능은 지속적인 또는 비연속적인
• 을 획득 방정식에서 구분 함수의 그래프
• 절대값으로 구분적으로 기능
• 구분적으로의 변환 기능
• 구분의 기능에 문제
• 더 연습

구분 함수(또는 조각-현명한 기능)은 그들이 무슨 이름: 하나의 그래프에 다른 기능(하위 기능)의 조각. 가장 쉬운 방법은 그들의 생각하는 경우 그린 더 이상의 기능을 그래프에서,당신은 단지 삭제하는 부품의 기능들을 가정하지 않는(을 따라\(x\)’s);그들은 다르게 정의를 위한 다양의 간격으로\(x\). \y(\)가 다르게 정의를 위해 서로 다른 값의\(x\);우리를 사용하여\(x\)을 간격에 있습니다,그래서 우리는 무엇을 찾을 수 있\y(\)가 수반되어야 합니다.여기서 inverses of Functions 섹션에서 piecewise 함수의 inverse 의 예가 있습니다.

Here’s an example and graph:

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (“if”대신”for”를 사용하고”if”대신 쉼표 또는 세미 콜론을 사용하는 등이를 표시하는 다른 방법이 있습니다.() 도메인:\(\mathbb{R},\,\,\,\text{or}\,\,\left({-\infty,\infty}\right)\) Range: \(\mathbb{R},\,\,\,\text{또는}\,\,\left({-\infty,\infty}\right)\)

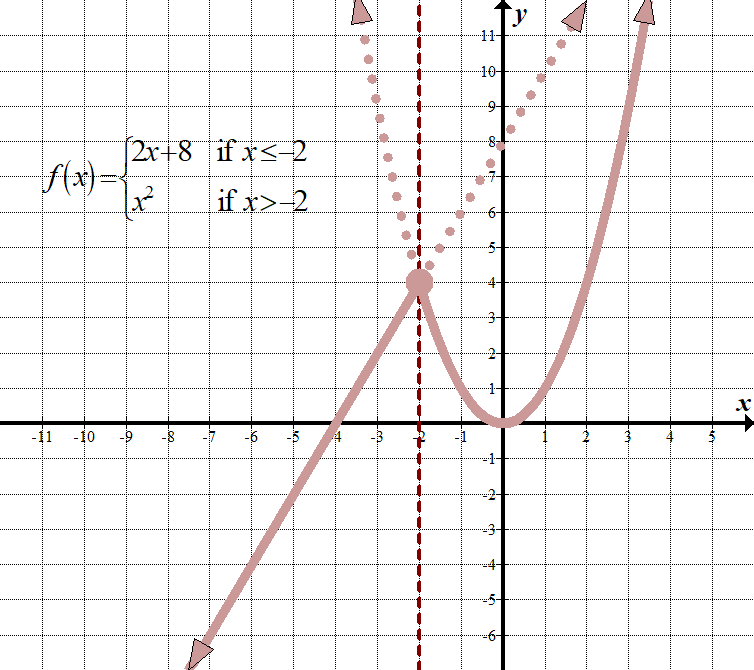이것이 무엇을 의미하는 모든\(x\)보다 작거나 같음 -2,우리가 필요한 그래프를 선\(2x+8\), 된 것처럼 보이지만 실제로는 유일한 기능에서 그래프입니다. -2 보다 큰 모든\(x\)값에 대해 그래프의 유일한 함수 인 것처럼\({{x}^{2}}\)를 그래프로 표시해야합니다. 그런 다음 우리가 필요로하지 않는 부분을”제거”해야합니다. 우리는 여전히 두 그래프의 기준점으로 원점을 사용한다는 것을 기억하십시오!

수직선\(x=-2\)가 두 그래프 사이의”경계”선으로 어떻게 작용하는지 보시겠습니까?

점\((-2,4)\)에는 닫힌 원이 있습니다. 기술적으로,그것은 단지에 속하\(2x+8\)기능을,이후 그 기능이 있는 보다 적거나 동등한 기호,그러나 이후 지점에\({{x}^{2}}\)그래프로,우리는 사용할 수 있습니다 닫히는 원형으로 나타나는 경우에 모두 기능입니다. 보시다시피,그렇게 나쁘지는 않습니까?

조각 단위 함수 평가

때때로 조각 단위 함수를 제공하고 평가하도록 요청합니다; 즉,\(x\)값이 주어지면\(y\)값을 찾으십시오. 그래프를 사용하지 않고\(x=-6\)및\(x=4\)에 대해이 작업을 수행합시다. 여기에는 함수를 다시:

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{맞춤}2x+8\,\,\,\,\,&\text{if}x\le-2\\{{x}^{2}}\,\,\,\,\,\,\,\텍스트{}\,&\text{if}x>-2\끝{맞춤}\right.\)

우리는 먼저에서 보고 싶은 조건에서의 오른쪽 첫째,시 우리의\(x\)입니다. \(X=-6\)일 때,우리는 그것이 -2 보다 작다는 것을 알고 있으므로\(x\)를\(2x+8\)에만 연결합니다. \(f(x)\)또는\(y\)는\((2)(-6)+8=-4\). 우리는\(\boldsymbol{{x}^{2}}\)에 대해서도 신경 쓰지 않습니다! 그렇게 쉽습니다. 위의 그래프를 사용하여 올바르게 수행했음을 알 수 있습니다. 나는 이것을 시도 할 수 없다. 우리는 먼저 오른쪽을보고 우리의\(x\)가-2 보다 크다는 것을 알 수 있으므로\({{x}^{2}}\)에 연결합니다. (우리는 이번에\(2x+8\)를 무시할 수 있습니다.)\(f(x)\)또는\(y\)는\({{4}^{2}}=16\).

조각 단위 함수 그래프 작성

조각 단위 함수를 그래프로 표시하라는 메시지가 표시됩니다. 때로는 그래프를 포함할 기능은 비,연속 또는 불연속을 의미하는 당신을 선택해야에서 연필 중간의 그래프 때 당신은 그것을 그리기(처럼 뛰어!). 연속 기능은 왼쪽에서 오른쪽으로 그려야한다면 연필을 집어 올릴 필요가 없다는 것을 의미합니다.그리고 그래프는 수직선 테스트를 통과 한 경우에만 진정한 함수라는 것을 기억하십시오.

이러한 단편적인 함수를 그려서 연속적인지 비 연속적인지 확인합시다. 우리가 각 함수를 유일한 것처럼 그리는 방법에 주목하고,필요하지 않은 부분을”지우기”하십시오. 대수 함수 섹션에서 여기에서했던 것처럼 도메인과 범위도 얻을 수 있습니다.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
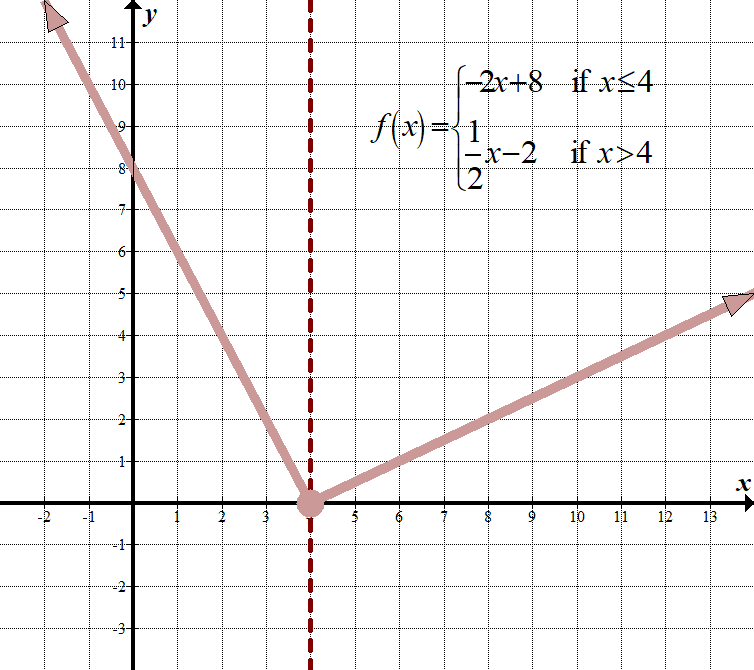\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

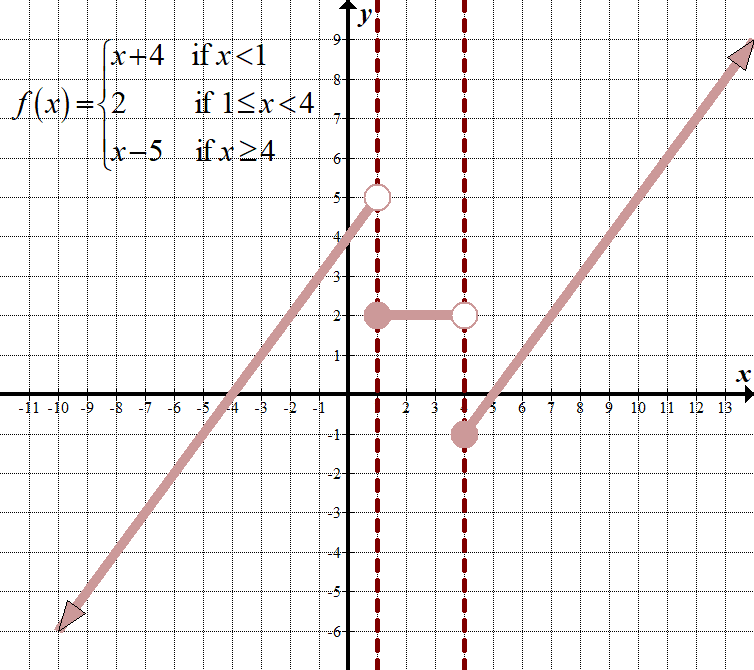We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: 여기 그래프.

를 넣어를 구분적으로 기능\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}x+4\,\,\,\,\,\,\,\,\,\텍스트{if}x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{1}\le x<4\\-5+x\,\,\,\,\,\텍스트{if}x\ge4\끝{array}\right.\)에서 계산기,을 입력할 수 있는 기능에 라인에 의해 나누어 기능에서 각 구간에 의해”시험 불평등”의 간격(보고 괄호 안!). 이유는 우리가 나눌에 의해 간격으로 또는 불평등이기 때문에 계산기를 반환하는 경우 1 불평등(예:\(x<1\))true;예를 들어,\((x+4)\)끝낼 것입\((x+4)/(1)\)면\(x<1\). \(X\ge1\)일 때 0 으로 나누므로 아무 것도 그려지지 않습니다. 다음은 우리가 계산기에 넣을 수있는 것입니다: \(\displaystyle\을 시작{array}{l}{{Y}_{1}}=\left({x+4}\right)/\left({x<1}\right)\\{{Y}_{2}}=\left(2\오른쪽)/\left({x\ge1\text{및}x<4}\right)\\{{Y}_{3}}=\left({-5+x}\right)/\left({x\ge4}\right)\끝{array}\) (주는 입력할 수도 있습니다 이에 한 줄을 곱하여 조건을 대신 나누어,그리고 사용하여 플러스 표지판 사이에 세 개의 각 기능/간격으로: \(\displaystyle{{Y}_{1}}=\left({x+4}\right)\left({x<1}\right)+\left(2\오른쪽)\left({x\ge1\text{및}x<4}\right)+\left({-5+x}\right)\left({x\ge4}\right)\).) 다음은 세 줄을 사용하기위한 키 입력입니다. 두 번째 수학(테스트)을 사용하여\(\le\),\(\ge\)등이있는 화면으로 이동합니다. 예를 들어,2 차 수학 6 은\(\le\)를 얻습니다. 두 번째 수학(테스트)을 사용하여\({{Y}_{2}}\)의”and”에 대해 논리에 대한 권리를 얻은 다음 1 을 사용하십시오.

는 방법을 말하면 구분의 기능은 지속적인 또는 비연속적인

는 경우를 구분적으로 그래프는 지속적인 또는 비연속, 당신이 볼 수 있는 경계에서 포인트를 참조하면\y(\)포인트가 같습니다. (\(Y\)의 다른 경우 그래프에”점프”가있을 것입니다!)

우리가 위에서 사용한 함수에 대해 이것을 시도해 봅시다:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the “boundary point”:나는 이것이 어떻게 작동하는지 잘 모르겠습니다.}-2(4)+8=0\\\,\,\,\프랙{1}{2}(4)-2=0\이 함수는 연속적 일뿐만 아니라 연속적 일 수도 있습니다.
\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{1}\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\텍스트{if}x\ge4\끝{array}\right.\)	함수의 처음 두 부분을 확인해 보겠습니다. 참고 두 번째 부분에서\(y\)는 항상 2 입니다: \(\을 시작{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) 이후\(5\ne2\),우리는 여기서 멈추고,이를 구분의 기능은 아닌 지속적입니다. \(Y\)’s 가 같으면\(x=4\)에서 다음 경계 점을 확인하기 위해 하나씩 가야 할 것입니다.

을 획득 방정식에서 구분 함수의 그래프

요청할 수 있습니다 쓰기연 기능이 주어진,그래프. 이제 우리는 단편적인 기능이 모두 무엇인지 알았으므로 그렇게 나쁘지는 않습니다!

을 검토를 구하는 방법 방정식에서 선형,그래프,보를 획득 방정식의 라인에서,그리고 이차 참조하십시오를 찾는 방정식에서 포인트 또는 그래프.

다음은 그래프이며,조각 별 방정식을 도출하는 방법에 대한 설명이 있습니다:

Piecewise Function Graph	Procedure to get Function
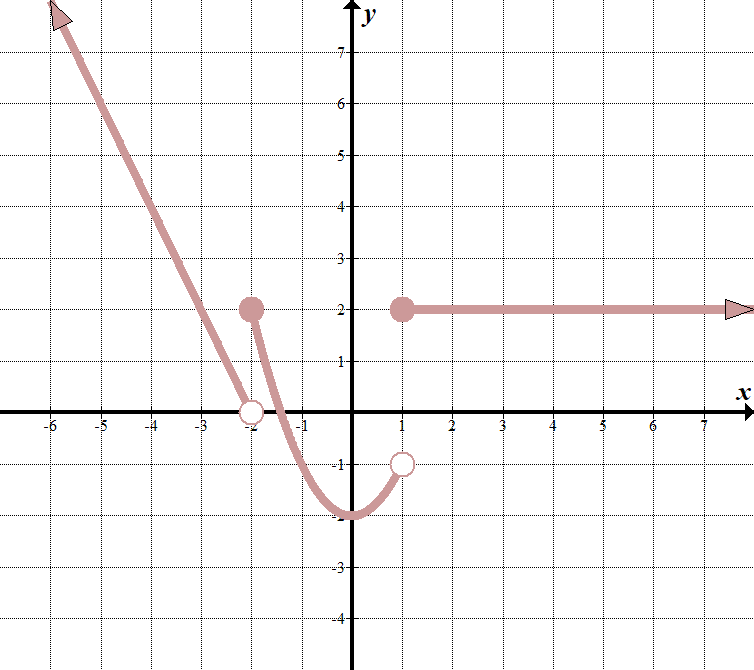	We see that our “boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\텍스트{ }……\,\,\,\,\,\,\,\,\텍스트{if}x<-2\\\텍스트{ }……\,\,\,\,\,\,\,\,\텍스트{if}-\text{2}\le x<1\\\텍스트{ }……\,\,\,\,\,\,\,\,\텍스트{if}x\ge1\끝{array}\right.\) 우리는 방정식\(y=-2x-4\)를 얻기 위해 가장 왼쪽 줄에\((-2,0)\)와\((-3,2)\)두 점을 선택할 수 있습니다. 중간 함수는\(y={{x}^{2}}-2\), 그리고 가장 오른쪽 함수는 단지 수평선\(y=2\)입니다. 따라서,단편적인 함수는: \(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}-2 배-4\,\,\,\,\,\,\,\텍스트{if}x<-2\\\text{}{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\텍스트{if}-\text{2}\le x<1\\\텍스트{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}x\ge1\끝{array}\right.\)
	우리는 우리의”경계선 라인”은\(x=5\). 선은\((5,4)\)에서 만나기 때문에\(\le\)또는\(\ge\)기호를 어디에 넣는지는 중요하지 않습니다; 우리는 단지 그것을 두 곳에 둘 수 없거나 기능이 아닐 것입니다. 우리는 지금까지: \(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\텍스트{ }……\,\,\,\,\,\,\,\,\,\텍스트{if}x<5\\\텍스트{ }……\,\,\,\,\,\,\,\,\,\텍스트{if}x\ge5\끝{array}\right.\) 다시 말하지만,우리는 그들의 방정식을 결정하기 위해 각 줄을 따로보아야합니다. 우리는 이것들을 얻기 위해 각 선에서 2 점을 취하거나 슬로프와\(y\)–인터셉트에서 파생 할 수 있습니다.: \(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\텍스트{if}x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\텍스트{if}x\ge5\끝{array}\right.\)

절대값으로 구분적으로 기능

작성할 수 있습니다 절대값 기능으로 구분 함수의–그것은 정말 멋지다! 이 주제를 계속하기 전에 절대 값 방정식과 부등식 해결을 검토하고 싶을 수 있습니다.

\(f\left(x\right)=\left|x\right|\)함수가 있다고 가정 해 봅시다. 에서 우리가 무엇을 배운 이전에 우리가 알고 있는 경우\(x\)은 긍정적인 때문에,우리는 절대값,그것은 여전히 그냥\(x\). 그러나\(x\)가 음수 일 때 절대 값을 취하면 절대 값이 양수가되어야하기 때문에 반대(부정)를 취해야합니다. 말이 되니? 예를 들어\(|5|\)가 있다면 양수이기 때문에 절대 부호 안에있는 것을 취합니다. 하지만\(|-5|\),우리는 반대로(부)무슨의 내부에는 절대 가치를 만들\(\displaystyle5\,\,\,(-\,-5=5)\).즉,이 절대 값 함수를 단편적인 함수로 쓸 수 있습니다. 절대 값 안에있는 것을 0 으로 설정하여”전환점”또는”경계점”을 얻을 수 있음을 알 수 있습니다. 그런 다음 해당 간격에서 절대 값없이 함수의 부호에 따라 원래 함수를 사용하거나 함수를 부정합니다.

예를 들어,우리가 할 수 있습 쓰기\(\displaystyle\left|x\오른쪽|\text{}=\left\{\을 시작{array}{l}x\,\,\,\,\,\,\,\,\,\텍스트{if}x\ge0\\-x\,\,\,\,\,\텍스트{if}x<0\끝{array}\right.\). 또한,함수의 경우는 연속(이 없다”이동”)에서 경계점,그것은 중요하지 않 우리가 어디를 넣어”보다 작거나 같음”(또는”보다 크거나 같음”)기호로 우리는 반복하지 말라 그들! 이론적으로 동일한\(x\)에 대해\(y\)의 두 값을 가질 수 없거나 함수가 없기 때문에 반복 할 수 없습니다.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the “boundary line”. 절대 값 안에있는 것을 0 으로 설정 한 다음\(\boldsymbol{x}\)에 대해 해결하여이 작업을 수행합니다. 때\(2x+3\ge0\),우리는 얻을\(\displaystyle x\ge-\frac{3}{2}\)(실제로,우리가 해결할 때\(\ge\)를 유지할 수 있습니다). \(2x+3\)가 양수일 때,우리는 단지”있는 그대로”가져 가지만,그것이 음수라면,우리는 전체를 부정해야합니다. 따라서 조각 단위 함수는: \(\displaystyle\left|{2x+3}\right|=\left\{\을 시작{array}{l}2x+3\,\,\,\,\,\,\,\,\,\텍스트{if}x\ge-\frac{3}{2}\text{}\\-2x-3\,\,\,\,\,\텍스트{if}x<-\frac{3}{2}\끝{array}\right.이 작업을 수행하려면 어떻게해야합니까?
\(f\left(x\오른쪽)=\left|{{{x}^{2}}-4}\right|\)	Let’s 처음 찾기”경계선(s)”;우리는 무엇을 설정 내부의 절대값은 0 입니다. 때\({{x}^{2}}-4\ge0\),우리는\(x\le-2\)또는\(x\ge2\)(일부를보십시오 숫자!). \({{X}^{2}}-4\)가 양수이면”있는 그대로”가져 가지만 음수이면 부정해야합니다. 구분의 기능은 다음과 같습니다. \(\displaystyle\left|{{{x}^{2}}-4}\right|=\left\{\을 시작{array}{l}{{x}^{2}}-4\,\,\,\,\,\텍스트{if}x\le-2\\4-{{x}^{2}}\,\,\,\,\,\텍스트{if}-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\텍스트{if}x\ge2\text{}\끝{array}\right.\)또는\(\displaystyle\left|{{{x}^{2}}-4}\right|=\left\{\을 시작{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\텍스트{if}x\le-2\text{}\,\,\text{또는}\,\,\text{}x\ge2\\4-{{x}^{2}}\,\,\,\,\,\,\,\텍스트{if}-2<x<2\끝{array}\right.\) 시(이후에 함수 이 지속적으로),사실은 그렇지 않습니다 문제는 우리가\(\le\)및\(\ge\)(반대하여\(<>\)),로 우리는 반복하지 않는다.
\(f\left(x\오른쪽)=2x+\left|{x+2}\right|\)	이 하나의 작은 난이도가 때문에,우리는\(x\)내부와 외부에서 절대적인 값입니다. “경계선”의 경우 절대 값 안에있는 것만 사용합니다. 때\(x+2\ge0\),우리는\(x\ge-2\). 그러나 단편적인 함수의 경우 절대 값 밖에있는 부분을 포함하여 전체 함수를 사용해야합니다. 따라서 단편적인 함수는: \(\displaystyle2x+\left|{x+2}\right|=\left\{\을 시작{array}{l}2x+x+2\,\,\,\,\,\텍스트{if}x\ge-2\\2x-x-2\,\,\,\,\,\텍스트{if}x<-2\끝{array}\right.\) 자 단순화: \(\displaystyle2x+\left|{x+2}\right|=\left\{\을 시작{array}{l}3x+2\,\,\,\,\,\,\,\텍스트{if}x\ge-2\\x-2\,\,\,\,\,\,\,\,\,\,\텍스트{if}x<-2\끝{array}\right.\) 보다 작고 큰 값을 시도하십시오.
\(g\left(x\오른쪽)=\left|{{{x}^{2}}-4-5}\right|\)	이 최상의 해결과 표시 차트 때문에 우리는 이차와 우리의 위치를 알 필요 기능은 긍정적이고 부정적이다. 먼저 절대 값 함수 내부의 2 차 값을\(\left({x-5}\right)\left({x+1}\right)\)로 팩터링합니다. 다음 사용하인 차트를 보는 요인은 긍정적이고 부정적인,기억하는 요인은 긍정적이,우리가 사용하는 기능”있는 그대로”,그리고는 요인은 부정적인,우리가 부정하는 기능: \(\displaystyle\left|{{{x}^{2}}-4-5}\right|=\left\{\을 시작{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}x\le-1\,\,\,\,\텍스트{또는}\,\,\,\,x\ge5\\-\left({{{x}^{2}}-4-5}\right)\,\,\,\,\텍스트{if}-1<x<5\text{}\끝{array}\right.\)
\(\displaystyle g\left(x\오른쪽)=\frac{{\left|{x+2}\right|}}{{x+2}}\)	이것은 합리적인 기능을,이후 거의 변수 여러 분야에 사용됩니다. 때\(x+2\ge0\),우리는\(\displaystyle x\ge-2\). 면\(x+2\)이 긍정적이,우리는 단지 그것을 가지고”있는 그대로”지만,경우의 음,우리가 부정에서 무엇을 절대값:\(\displaystyle\frac{{\left|{x+2}\right|}}{{x+2}}=\left\{\을 시작{array}{l}\frac{{x+2}}{{x+2}}\,\,\,\,\,\,\,\,\,\텍스트{if}x\ge-2\\\frac{{x2}}{{x+2}}\,\,\,\,\,\,\텍스트{if}x<-2\끝{array}\right.\). 그러나\(x\ne2\)(도메인 제한:분모는 0 이 될 것임)때문에 조심해야합니다. 따라서 조각 단위 함수는: \(\displaystyle\frac{{\left|{x+2}\right|}}{{x+2}}=\left\{\을 시작{array}{l}1\,\,\,\,\,\,\,\,\,\,\텍스트{if}x>-2\\-1\,\,\,\,\,\,\텍스트{if}x<-2\끝{array}\right.\).

를 제출하도록 요청 받으실 수도 있습을 절대값을 그래프에 쓰고 그것으로 구분적으로 기능:

Absolute Value Graph	Method to get Piecewise Function
	We see that our “boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). 절대 값 함수가있는 경계선을 얻으려면 절대 값 안에있는 것을 0 으로 설정하고\(x\)에 대해 해결하기 때문입니다). \(x>0\)일 때,우리는 선의 방정식이\(y=2x-2\)임을 알 수 있습니다. 이 방정식은 다음과 같습니다. 을 작성할 수 있습니다 이것으로 구분적으로 기능: \(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}2x-2\,\,\,\,\,\,\,\텍스트{if}x>0\\-2x-2\,\,\,\text{if}x\le0\끝{array}\right.\) 우리는 또한이 변형된 절대값 기능:\(y=2\left|x\오른쪽|-2\)또는\(y=\left|{2x}\right|-2\)(이후 2 은 긍정적 인,그것은 내부 또는 외부\(\left|{\,\,}\right|\)). (이 말이기 때문 안에 무엇\(\left|{\,\,}\right|\)은\(>0\),우리가 사용하여 정기적인 기능\(y=2x-2\),그리고 무엇을 할 때의 내부에는\(<0\), 우리는 부정 절대값 부분을 확인 그것은\(y=-\left({2x}\right)-2\)).
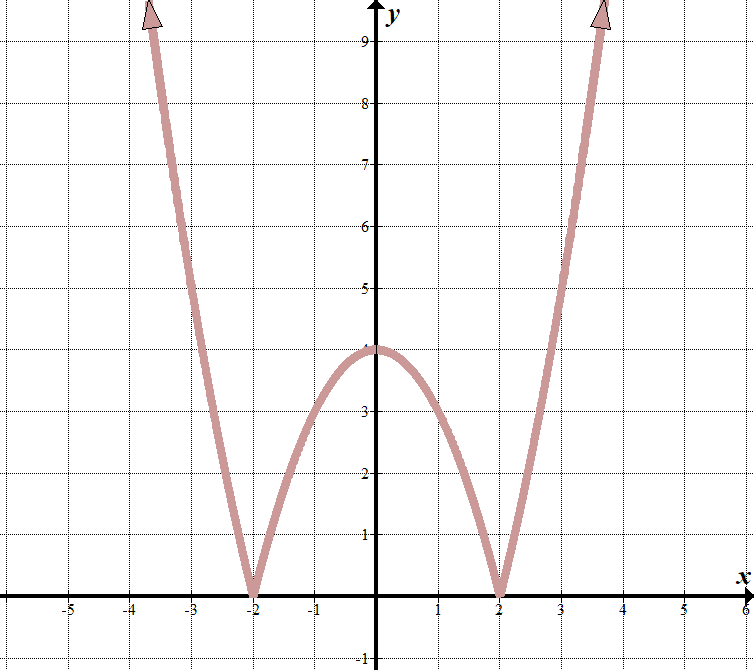	우리는 우리의”경계선은”에\(x=2\)및\(x=-2\),그래서 무엇이 내부에는 절대 값을 등록해야 하는 요인의\(x2\) 와\(x+2\). 때\(x<-2\)또는\(x>2\),우리가 볼 수 있는 그래프와 같이 정상적인 부분의 그래프\(y={{x}^{2}}-4\). (나는 요인을 알고 좋은 추측을 취함으로써 이것을 알아 냈습니다! 을 때)\(-2<x<2\),방정식은,반전이나 부정(뒤집어의\(x\)-axis). 을 작성할 수 있습니다 이것으로 구분적으로 기능: \(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\텍스트{if}x<-2\text{또는}x>2\\-{{x}^{2}}\텍스트{+ 4}\,\,\,\,\,\,\텍스트{if}-2\le x\le2\끝{array}\right.\) 우리는 볼 수 있습니다 이 시작했 변형 이차 기능\(y={{x}^{2}}-4\)절대값으로 주위에,그것 때문에 모든\y(\)값은 긍정적인:\(y=\left|{{{x}^{2}}-4}\right|\).
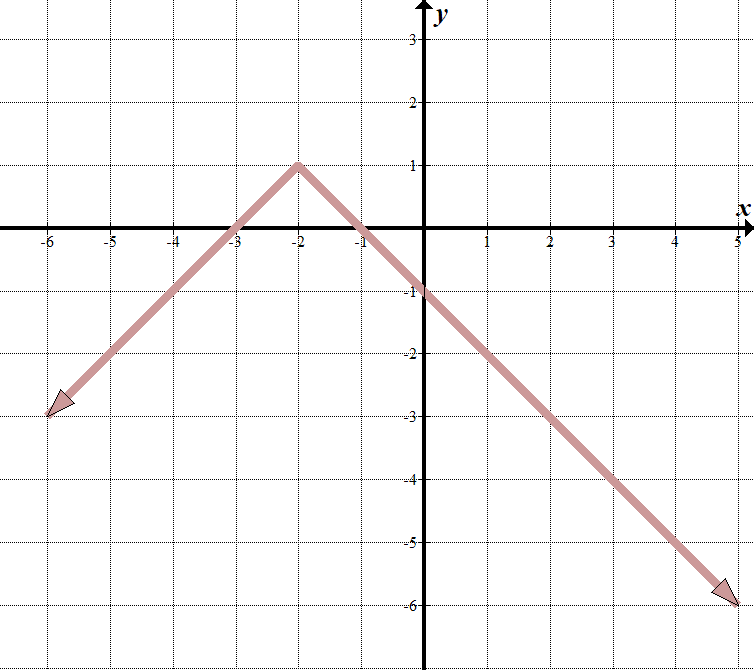	우리는 우리의”경계선 라인”은\(x=-2\),그래서 무엇이 내부에는 절대 값을 등록해야 합\(x+2\). \(x>-2\)일 때,우리는 선의 방정식이\(y=-x-1\)임을 알 수 있습니다. 이 경우 해당 행은 다음과 같습니다. 을 작성할 수 있습니다 이것으로 구분적으로 기능: \(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}x-1\,\,\,\,\,\,\텍스트{if}x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\텍스트{if}x\le-2\끝{array}\right.\) 아마도 이것을 변환 된 절대 값 함수로 쓰는 것이 더 쉬울 것입니다. 우리는 부모 절대 값 함수가 수직으로 뒤집혀 왼쪽 2 로 이동하고 1 위로 이동한다는 것을 알 수 있습니다. 우리의 절대 값 방정식은\(y=-\left|{x+2}\right|\,\,+\,\,1\). 이것은 위의 단편적인 함수와 동일합니다. 그것을 시도하십시오-작동합니다!

Piecewise 함수의 변환

piecewise 함수의 변환을 수행합시다. 여기 부모 그래프 및 변환 섹션에서 부모 함수와 그 변환에 대한 방법을 배웠습니다. 단편적인 변환을 시도하기 전에이 섹션을 먼저 읽고 싶을 것입니다.

자 변형은 다음과 같은 구분적으로 기능을 뒤집위\(x\)-축에 수직으로 뻗어에 의해 요인의 2 단위,단위 1 을 오른쪽 단위 3 니다.

우리는 우리 것을 그릴\(-2f\left(x1\오른쪽)+3\),where:

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{맞춤}x+4\,\,\,\,\,\,\,\,&\text{if}x<&\text{1}\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{if}x\ge4\끝{맞춤}\right.\)

변환을 위해 t-차트를 채울 때”경계”점을 사용하는지 확인합시다. 괄호 안의 변환은\(x\)(반대 수학 수행)로 수행되고 외부는\(y\)로 수행된다는 것을 기억하십시오. 아래 표와 같이 t-차트를 생각해 내기 위해 각”경계선”에 두 점을 포함하여 키 포인트를 사용할 수 있습니다.

주기 때문에 이 변화는 것은 복잡하고,우리는 우리와 함께 올 수 있는 새로운 구분적으로 기능에 의해 변형 3″”조각한 변화는”\(x\)”s 는 경계점(추가 1 또는 오른쪽으로는 1)이후,우리는 반대 수학에 대해”\(x\)”s. 각 간격에서 새로운 함수를 얻으려면 원래 방정식에서”\(x\)”에 대해”\(x-1\)”를 대체하고-2 를 곱한 다음 3 을 더하면됩니다. 예를 들어\(\displaystyle-2f\left({x-1}\right)+3=-2\left+3=-2\left({x+3}\right)+3=-2x-3\).

\(\displaystyle-2f\left({x1}\right)+3=\left\{\을 시작{array}{l}-2\left({\left({x1}\right)+4}\right)+3=-2x-3,\,\,\,\,\텍스트{if}x-1<1\,\,\,\left({x<2}\right)\\-2\left(2\right)+3=-1,\,\,\,\,\텍스트{if}\,\text{2}\le x<5\\-2\left({\left({x1}\right)-5}\right)+3=-2x+15,\,\,\,\,\텍스트{if}x\ge5\끝{array}\right.\)

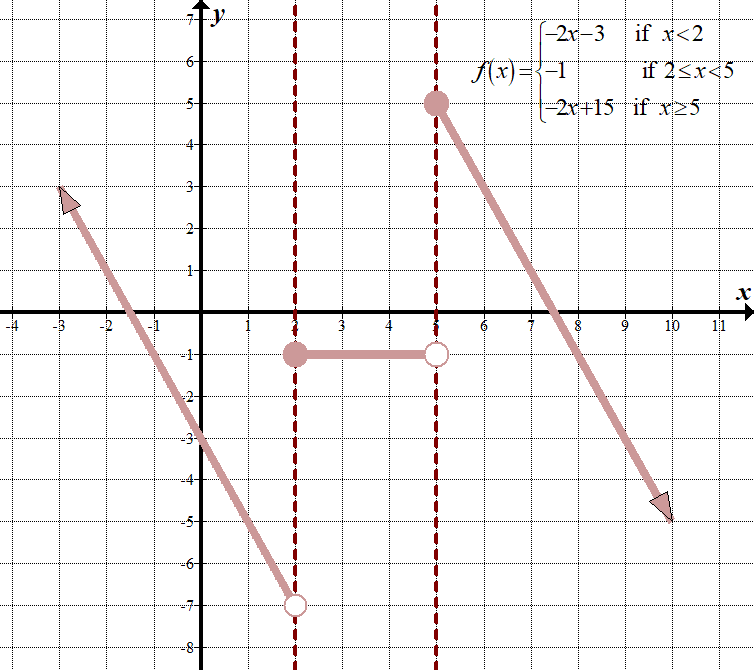
다음은 t 차트를 포함한”이전”및”이후”그래프입니다:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

좋아하는 개 그루머는 강아지의 체중에 따라 요금을 부과합니다. 개가 15 파운드 이하인 경우 그 루머는 35 달러를 청구합니다. 당신의 개가 15 파운드에서 40 파운드 사이라면,그녀는 40 달러를 청구합니다. 당신의 개가 40 파운드 이상인 경우,그녀는 40 달러를 부과하고 각 파운드마다 2 달러를 추가로 부과합니다.

(a)개 그루머가 청구하는 것을 설명하는 단편적인 함수를 작성하십시오.

(b)함수를 그래프로 나타냅니다.

(c)귀여운 강아지의 체중이 60 파운드 인 경우 그 루머는 무엇을 청구합니까?

솔루션:이것이 가격이 변하는 가중치이기 때문에”경계점”이 15 와 40 임을 알 수 있습니다. 우리는 두 개의 경계점을 가지고 있기 때문에,우리는 우리의 단편적인 함수에 세 가지 방정식을 가질 것입니다. 우리는 개가 0 파운드 이상 무게가 나가야하기 때문에 0 에서 시작해야합니다:

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\텍스트{ }……\,\,\,\,\,\,\,\,\,\텍스트{if}0<x\le15\\\텍스트{ }……\,\,\,\,\,\,\,\,\,\텍스트{if}15<x\le40\\\텍스트{ }……\,\,\,\,\,\,\,\,\,\텍스트{if}x>40\끝{array}\right.\)

우리는 우리를 찾고 있다”대답”(얼마나 손질 비용)을”질문에”(얼마나 많은 무게 개)한 범위의 가격입니다. 처음 두 가지는 단지 정액 수수료(각각 35 달러와 40 달러)입니다. 마지막 방정식은 조금 까다 롭습니다; 그 루머는 40 파운드마다$40 플러스$2 를 청구합니다. 진짜 숫자를 시험해 봅시다:당신의 개가 60 파운드의 무게라면,그녀는$40 플러스$2 배\(20(60-40)\)를 청구 할 것입니다. 우리는 이것을 방정식으로 바꿀 것입니다:\(40+2(x–40)\),이는\(2x–40\)로 단순화됩니다(기울기는 어떻게 2 입니까?).

전체 조각 함수는:

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\텍스트{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}0<x\le15\\\텍스트{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}15<x\le40\\\text{}40+2\left({x40}\right)\,\,\,\,\,\,\텍스트{if}x>40\끝{array}\right.\)또는\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\텍스트{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}0<x\le15\\\텍스트{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}15<x\le40\\\text{}2x-40\,\,\,\,\,\,\,\텍스트{if}x>40\끝{array}\right.\)

(b)그래프하자:이 단편적인 방정식은 비 연속적임을 주목하십시오. 또한 주당 도메인 이 문제가 될 수 있습\(\left({0,200}\right]\)(주지 않는 무게가 200 파운드!)및 합리적인 범위는\(\왼쪽\컵\왼쪽\)일 수 있습니다.강아지의 체중이 60 파운드라면 그래프나 함수를 사용하여 80 달러를 내야한다는 것을 알 수 있습니다. 우와! 그것은 인간의 이발(적어도 내 이발)보다 더 많은 비용이 듭니다!

문제:

당신은 그녀가 사랑하는 수학 티셔츠를 기금 모금 행사로 판매 할 계획입니다. 도매 티셔츠 회사는 처음 75 개의 셔츠에 대해 10 달러의 셔츠를 청구합니다. 처음 75 개의 셔츠를 구입 한 후 최대 150 개의 셔츠를 구입하면 회사는 셔츠 당 7.50 달러로 가격을 낮출 것입니다. 150 개의 셔츠를 구입 한 후 가격은 셔츠 당 5 달러로 줄어 듭니다. 이 상황을 모델링하는 함수를 작성하십시오.이것은 가격이 바뀌는 곳에서 구입 한 티셔츠의 수이기 때문에”경계점”이 75 와 150 이라는 것을 알 수 있습니다. 우리는 두 개의 경계점을 가지고 있기 때문에,우리는 우리의 단편적인 함수에 세 가지 방정식을 가질 것입니다. 우리는 적어도 하나의 셔츠를 구입한다고 가정하기 때문에\(x\ge1\)로 시작할 것입니다. 참고 이 문제에서 구입 한 티셔츠 수(\(x\))또는 도메인은 정수이어야하지만이 제한은 문제의 결과에 영향을 미치지 않아야합니다.

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\text{}……\텍스트{if}1\le x\le75\\\text{}……\텍스트{if}75<x\le150\\\text{}……\텍스트{if}x>150\끝{array}\right.\)

우리는 우리를 찾고 있다”대답”(총 비용의 티셔츠는)”질문에”(얼마나 많은 구입하는)한 범위의 가격입니다.

최대 75 개의 셔츠를 포함하여 가격은$10 이므로 총 가격은\(10x\)입니다. 75 개 이상의 셔츠이지만 최대 100 개의 셔츠의 경우 비용은 7.50 달러이지만 처음 75 개의 티셔츠는 여전히 셔츠 당 10 달러입니다. 두 번째 기능에는 처음 75 개의 셔츠(75 회$10)에 지출 된$750 이 포함되며\((x-75)\)인 75 세 이상의 셔츠 수의$7.50 배도 포함됩니다. 예를 들어,80 개의 셔츠를 구입 한 경우\(\$10\번 75=\$750\),\(\$7.50\번 5\,\) (80 – 75) 75 번째 셔츠 이후의 셔츠.

마찬가지로 150 개가 넘는 셔츠의 경우 여전히 75 개의 셔츠 인$7 을 통해$10 의 가격을 지불합니다.50 셔츠 76~150 개(셔츠 75 개 이상)의 가격은 150 개 이상 구입 한 셔츠 수에 대해 셔츠 당 5 달러입니다. 우리는 지불 할 것이다\(10(75)+7.50(75)+5(x-150)\)\(x\)셔츠의 경우. 숫자에 넣고 그것을 시도!

전체 구분의 기능은 다음과 같습니다.

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\text{}10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}1\le x\le75\\\text{}7.5x\text{}+\텍스트{ }187.5\,\,\,\,\,\텍스트{경우 7}5<x\le150\\\text{}5x+562.5\,\,\,\,\,\,\,\,\,\,\텍스트{if}x>150\end{array}\right.\)또는\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\text{}10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}1\le x\le75\\\text{}7.5x\text{}+\텍스트{ }187.5\,\,\,\,\,\텍스트{경우 7}5<x\le150\\\text{}5x+562.5\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}x>150\끝{array}\right.\)

문제가:

버스 서비스 비용은$50 을 위한 첫 번째 400 마일,그리고 각각의 추가 300 마일(또는 일부분)에 추가합$10 운 식사를 제공합니다.

거리 측면에서 버스 요금을 마일 단위로 나타내는 단편적인 함수를 사용합니다.이것은 실제로 까다로운 문제이지만 먼저 400 인”경계점”에 대해 먼저 생각해 봅시다. 타는 것이 400 마일 미만일 때 꽤 간단합니다;비용은$50 입니다.

에 대한보다 큰 400 마일을,우리는 빼야하는 첫 번째 400 마일(하지만 기억을 포함하는 첫 번째$50),나눌 수의 마일에 의해 왼쪽 300miles(라운드까지,가 있다면 분수액),곱해$10.

까다로운 부분은 우리가 다음 300 마일의 일부를”반올림”할 때입니다. 우리가 사용할 수 있습니다”천장”기능(정하여 지정\(\left\lceil{}\right\rceil\));이 기능은 적어도 정수보다 크거나 같음을 입력;예를 들어,천장 모두의 3.5 4 은 4 입니다.이것이 우리가 가지고있는 것입니다:

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}\text{}50\텍스트{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\텍스트{if}0\le x\le400\\\text{}50+10\번\left\lceil{\frac{{x-400}}{{300}}} \오른쪽\rceil\텍스트{ }\,\,\,\,\,\,\텍스트{if}x>400\끝{array}\right.\)

해보자! 만약 우리가 1500 마일 타고,비용을 것\(\displaystyle50+10\번\left\lceil{\frac{{1500-400}}{{300}}} \오른쪽\rceil\text{}=50+10\번 4=\$90\).

문제:

\(\boldsymbol{a}\)의 어떤 값이이 단편적인 함수를 연속적으로 만들까요?

\(\displaystyle f\left(x\오른쪽)=\left\{\을 시작{array}{l}3{{x}^{2}}+4\,\,\,\,\,\텍스트{if}x<-2\\5x+\boldsymbol{a}\,\,\,\,\,\,\,\,\텍스트{if}x\ge-2\끝{array}\right.\)

솔루션:

에 대한 구분적으로 기능을 지속적,경계에서점(여기서 기능을 변화),두\y(\)값이 같아야 합니다. 우리는 플러그인에서 2\(x\)모두에서 기능 및 확인\y(\)’s 는 동

\(\을 시작{맞춤}3{{x}^{2}}+4&=5 배+a\\3{{\left({-2}\right)}^{2}}+4&=5\left({-2}\right)+a\\12+4&=-10+a\\a&=26\끝{맞춤}\)

경\(a=26\)를 구분의 기능은 지속적인!

이 규칙을 배우고,연습,연습,연습!

더 많은 연습:아래의 Mathway 위젯을 사용하여 단편적인 함수를 작성하십시오. 제출(문제의 오른쪽에있는 파란색 화살표)을 클릭하고 절대 값을 단편적으로 쓰기를 클릭하면 답을 볼 수 있습니다.

입력할 수도 있습니에서 자신의 문제 또는 클릭 세 가지 점에서 오른쪽 상단 모서리를 클릭에서”예”을 드릴다운하여 주제입니다.

면 탭을 클릭합 보기 단계거나 여기를 클릭하여 등록할 수 있습에서 스냅 무료 평가판,및 그 후 업그레이드를 유료 구독에서 어떤 시간에(어떤 유형의 수학 문제를 해결합니다!).

행렬과 행렬을 가진 해결 시스템에-당신은 준비가되었습니다!