Konigsberg 는 18 세기에 독일 마을 이었지만 지금은 러시아 인 Preger 강에있는 마을입니다. 마을 내에는 7 개의 다리가있는 은행에 연결된 2 개의 섬이 있습니다(아래 그림과 같이).

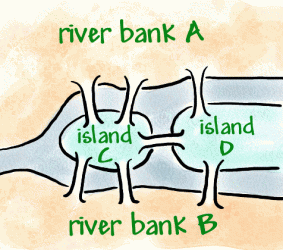
되었다는 전통 산책하려고 도시의 주위에 방법으로 thatonly 넘어 각각 다리를 한 번 있지만,그것을 입증 difficultproblem. 레온하르트 성당,오일러,스위스 수학자로서 서비스의 러시아 황후 Catherine 한,들에 대한 문제입니다.1736 년 오일러는 산책을 할 수 없다는 것을 증명했다. 그는 네트워크라고하는 일종의 다이어그램을 발명하여이를 증명했습니다.꼭지점(선이 만나는 점)과 호(선)로 구성됩니다.

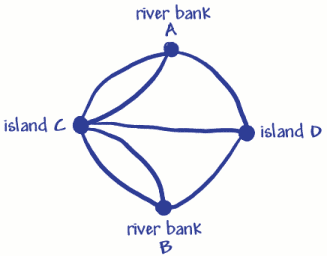
그는 네 개의 점(정점)두 강변 및 twoislands. 이들은 a,B 및 C,D 로 표시되었습니다.7 개의 선(호)은 7 개의 다리입니다. 3 개의 교량(호)이 강둑 A 에 합류하고 3 개의 교량(호)이 강둑 B 에 합류하는 것을 볼 수 있습니다. 즉,모든 정점에는 홀수 개의 호가 있으므로 oddvertices 라고합니다. (짝수 꼭지점은 짝수 호를 가져야 할 것입니다.)
문제는 eachbridge 를 횡단하는 마을을 한 번만 여행하는 것이 었음을 기억하십시오. 오일러의 네트워크에서 이것은 각각을 추적하는 것을 의미했습니다.한 번만 모든 정점을 방문하십시오. 오일러는 당신이 그 꼭지점에서 여행을 시작하거나 끝내기 위해 이상한 꼭지점을 갖기 위해 운동했기 때문에 할 수 없다는 것을 증명했습니다. (그것에 대해 생각해보십시오).하나의 시작과 한쪽 끝 만있을 수 있기 때문에 한 번만 eacharc 를 추적 할 수 있다면 두 개의 홀수 꼭지점이있을 수 있습니다. 다리 문제에는 4 개의 이상한 꼭지점이 있기 때문에 할 수 없습니다! 이상한 꼭지점이 없으면 어떻게됩니까?모두? 이 네트워크를 추적 할 수 있습니까?

본 발명의 네트워크 시작 새로운 유형의 형상 calledTopology. 토폴로지는 이제 계획을 포함하여 여러 가지 방법으로 사용됩니다.및 철도 네트워크 매핑. (아! 기차는 안으로 와야했다.그것….)