이해 한 후 지수 함수,우리의 다음 목표는 자연 로그.

주어진 방법을 자연 로그인이 설명한 수학에서 책,거기 작은””자연적인에 대한 그것은:그것은으로 정의 역$e^$x,이는 충분히 지니다.그러나 신선하고 직관적 인 설명이 있습니다:자연 로그는 일정 수준의 성장에 도달하는 데 필요한 시간을 제공합니다.

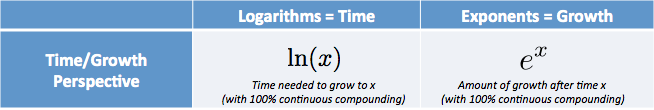
이 있다고 가정한 투자에서 구미 곰(who 하지 않는 이유는 무엇입니까?)연간 100%의 이자율로 지속적으로 성장합니다. 10 배의 성장을 원한다면 연속 복리를 가정하면$\ln(10)$또는 2.302 년만 기다릴 것입니다. 왜 10 배의 성장을 얻는 데 몇 년 밖에 걸리지 않는지 모르십니까? 패턴이 1,2,4,8 이 아닌 이유를 모르십니까? E 에 대해 자세히 읽어보십시오.

e 와 자연 로그는 쌍둥이입니다.

• $e^x$는 1 에서 시작한 후 우리가 가지고있는 금액입니다.0 고 지속적으로 성장을 위해$x$의 단위 시간
• $\ln(x)$(자연 로그)은 시간에 도달하는 금액이$x$고 가정하면,우리가 성장을 지속적으로서 1.0

너무 나쁘지 않죠? 수학자들이 당신에게 길고 기술적 인 설명을하기 위해 출격하는 동안,직관적 인 것에 뛰어 들자.

E 는 성장에 관한 것입니다

숫자 e 는 지속적인 성장에 관한 것입니다. 우리가 본 바와 같이 마지막 시간,$e^x$할 수 있습 병합 평가하고 시간:3 년간 100%성장과 같은 1 년에서 300%증가할 때,지속적으로 배합.

우리는 속도와 시간의 조합(4 년 동안 50%)을 취하고 편의를 위해 속도를 100%로 변환 할 수 있습니다(2 년 동안 100%제공). 로 변환하여 속도의 100%,우리만 생각하는 시간에 대해 구성 요소:

직관적으로, $e^x$의미합니다:

• 얼마나 성장 do I get 후 x 시간 단위(100%지속적인 성장)
• 예를 들어:후 3 시간 기간 동안 나는$e^3$=20.08 번의 양이”콘텐츠”로되어 있습니다.

$e^x$는 스케일링 팩터로,$x$단위 시간 후에 얼마나 많은 성장을 얻을 수 있는지를 보여줍니다.

자연 로그는 시간에 관한 것입니다

자연 로그는$e^x$의 역수이며 반대의 멋진 용어입니다. 공상에 대해 말하면,라틴어 이름은 logarithmus naturali 이며,약어 ln 을 제공합니다.

이제이 역 또는 반대 물건은 무엇을 의미합니까?

• $e^x$는 우리가 시간에 연결하고 성장을 얻을 수 있습니다.
• $\ln(x)$를 사용하면 성장을 연결하고 걸리는 시간을 얻을 수 있습니다.

예:

• $e^3$는 20.08 입니다. 3 단위의 시간이 지나면 우리는 20 으로 끝납니다.우리가 시작한 08 배.
• $\ln(20.08)$는 약 3 입니다. 20.08 의 성장을 원한다면 3 단위의 시간을 기다릴 것입니다(다시 100%연속 성장률을 가정).

나와 함께? 자연 로그는 우리에게 우리가 원하는 성장을 명중하는 데 필요한 시간을 제공합니다.

대수 산술은 정상이 아닙니다

전에 로그를 연구했는데 이상한 짐승이었습니다. 그들은 어떻게 곱셈을 덧셈으로 바꾸었습니까? 뺄셈으로 나누기? 보자.나는 이것을 할 수 없다. 직관적으로 질문은:현재 금액의 1 배를 얻기 위해 얼마나 오래 기다려야합니까?

제로. 지퍼. 나다. 당신은 이미 1 배의 현재 금액입니다! 1 에서 1 로 성장하는 데 시간이 걸리지 않습니다.이 경우 분수 값은 어떻게 계산됩니까? 얼마나 얻을 1/2 내 현재 금액? 100%로 지속적으로 성장하고 있다고 가정하면$\ln(2)$가 두 배가되는 시간이라는 것을 알고 있습니다. 우리가 그것을 역전 시키면(즉,부정적인 시간을 가져라)우리는 현재 가치의 절반을 가질 것입니다.

• $\ln(.나는 이것을 알아 냈다.693$

는 의미가 있습니다. 우리가 거꾸로 가면.693 단위(부정적인 초,가정 해 봅시다)우리는 현재 금액의 절반을 가질 것입니다. 일반적으로 분수를 뒤집어서 음수를 취할 수 있습니다:$\ln(1/3)=–\ln(3)=-1.09$. 즉,1.09 단위의 시간을 거슬러 올라가면 지금 가지고있는 것의 3 분의 1 이됩니다.

좋아,음수의 자연 로그는 어때? 당신의 박테리아 식민지를 1 에서-3 까지”성장”시키는데 얼마나 많은 시간이 걸립니까?

그것은 불가능합니다! 당신은 박테리아의”부정적인”양을 가질 수 없습니다,그렇죠? 대부분의(어…적어도)당신은 0 을 가질 수 있지만,작은 동물의 음의 양을 가질 수있는 방법은 없습니다. 부정적인 박테리아는 단지 이해가되지 않습니다.

• $\ln(\text{부정적인 수})=\text{정의되지 않은}$

정의되지 않은 다 의미 없다”고 양의 시간을 기다릴 수 있을 얻기 위해”부정적인 금액입니다. (글쎄,우리가 가상의 지수를 사용한다면 해결책이 있습니다. 그러나 오늘은 그것을 현실로 유지합시다.)

대수 곱셈은 강력한 재미

현재 금액의 9 배를 늘리는 데 얼마나 걸립니까? 물론,우리는 단지 ln(9)을 사용할 수 있습니다. 그러나 그것은 너무 쉽습니다,달라지자.

우리는 9x 성장을 3 배($\ln(3)$시간 단위를 취함)로 간주 한 다음 다시 3 배(다른$\ln(3)$시간 단위를 취함)로 간주 할 수 있습니다.:

• 9x 성장 시간=$\ln(9)$=다시 트리플 및 트리플 시간=$\ln(3)+\ln(3)$

흥미 롭습니다. 20 과 같은 모든 성장 수는 2 배의 성장이 뒤 따르는 10 배의 성장으로 간주 될 수 있습니다. 또는 4 배의 성장이 이어지고 5 배의 성장이 뒤 따른다. 또는 3 배 성장 다음에 6.666 배 성장. 패턴을 보시겠습니까?이 작업을 수행 할 때 로그가 어떻게 작동하는지 잘 모르겠습니다. 이 관계는 성장할 시간면에서 생각할 때 의미가 있습니다.

우리가 30 배 성장하고 싶다면 한 번에$\ln(30)$를 기다리거나 단순히$\ln(3)$를 3 배로 기다린 다음$\ln(10)$를 기다려 다시 10 배 성장할 수 있습니다. 순 효과는 동일하므로 순 시간도 동일해야합니다(그리고 그렇습니다).

분열은 어때? $\ln(5/3)$의미:5 번 성장하고 그 중 1/3 을 차지하는 데 얼마나 걸립니까?

음,5 번 성장하는 것은$\ln(5)$입니다. 성장하는 1/3 은$-\ln(3)$시간 단위입니다. 그래서

• $\ln(5/3)=\ln(5)–\ln(3)$

말하는 성장:5 시간으로 돌아가기””시간이 있을 때까지 세 번째는,그래서 당신은 왼쪽으로 5/3 성장이다. 일반적으로 우리가

• $\ln(a/b)=\ln(a)–\ln(b)$

I hope 이상한 수학의 로그를 시작해: 성장의 곱셈은 시간의 덧셈이되고,성장의 나눗셈은 시간의 빼기가됩니다. 규칙을 암기하지 말고 이해하십시오.

를 사용하여 자연 로그는 모든 비율

“확실히,당신이 말하는”,”이 문제점을 파악하고 작동을 위한 100%년 성장을 하지만 무엇에 대해 5%나는 일반적으로 얻는가?”

그것은 문제가되지 않습니다. 우리가$\ln()$에서 돌아 오는”시간”은 실제로 우리의$e^x$방정식에서”x”인 속도와 시간의 조합입니다. 우리는 단지 그것을 간단하게하기 위해 100%를 가정하지만 다른 숫자를 사용할 수 있습니다.

우리가 30 배 성장을 원한다고 가정 해보십시오:$\ln(30)$를 연결하고 3.4 를 얻으십시오. 이는 다음을 의미합니다:

• $e^x=\text{성장}$
• $e^{3.4}=30$

고 직관적으로 이 방정식의 의미는”100%반환을 위해 3.4 년 30x 성장”. 우리가 고려할 수 있는 방정식을 수 있:

우리는 수정할 수 있습니다”률”과”시간”한,평가*시간=3.4. 예를 들어,30 배의 성장을 원한다고 가정하십시오—5%의 수익을 가정 할 때 얼마나 오래 기다려야합니까?

• $\ln(30)=3.4$
• $\text{rate}*\text{time}=3.4$
• $.05*\text{time}=3.4$
• $\text{time}=3.4/.05=68\text{years}$

직관적으로”$\ln(30)=3.4$라고 생각하므로 100%성장시 3.4 년이 걸릴 것입니다. 내가 성장 속도를 두 배로 늘리면 필요한 시간을 반으로 줄입니다.”

• 3.4 년 동안 100%=1.0*3.4=3.4
• 1.7 년 동안 200%=2.0*1.7=3.4
• 6.8 년 동안 50%=0.5*6.8=3.4
• 68 년 동안 5%=.05*68=3.4

쿨,어? 자연 로그 사용할 수 있습니다 어떤 금리 또는 시간 만큼 그들의 제품 동일. 원하는 변수를 모두 흔들 수 있습니다.

멋진 예:규칙의 72

72 의 규칙은 정신 수학을 바로 가기를 추정하는 데 필요한 시간을 두 번 돈입니다. 우리는 그것을 도출 할 것입니다(예!)그리고 더 나은,우리는 그것을 직관적으로 이해할 것입니다.매년 100%이자로 돈을 두 배로 늘리는 데 얼마나 걸립니까?

어 오. 우리는 연속 요금에 대한 자연 로그를 사용 해왔다,하지만 지금은 연간 관심을 요구하고있다? 이것이 우리의 공식을 엉망으로 만들지 않을까요? 네,그것은 것입니다,하지만 합리적인 금리에 다음과 같 5%,6%또는 15%,많지 않으니 사이에 차이 매년 합성과 완전히 지속적인 관심사이다. 그래서 거친 공식은,어,대략 작동하고 우리는 우리가 완전히 지속적인 관심을 얻고있는 척 할 것입니다.

이제 질문은 쉽습니다:얼마나 오래 100%이자로 두 배가됩니까? ln(2)=.693. 그것은 걸립니다.693 단위의 시간(이 경우 년)은 100%의 비율로 연속 복리로 돈을 두 배로 늘립니다.

좋아,우리의 관심이 100%가 아니라면 5%또는 10%라면 어떨까요?

간단합니다. 만큼 속도*시간=.693,우리는 돈을 두 배로 늘릴 것입니다:

• rate*time=.693시간=.693/rate

그래서 우리가 10%성장 만했다면 걸릴 것입니다.693 / .10 또는 6.93 년 두 배로.

사물을 단순화하기 위해 100 을 곱하면 10 에 대해 이야기 할 수 있습니다.10:

• 시간을 두 배로=69.3/속도,여기서 비율은 퍼센트로 가정합니다.

이제 5%성장으로 두 배가되는시기는 69.3/5 또는 13.86 년입니다. 그러나 69.3 은 가장 나눌 수있는 숫자가 아닙니다. 2,3,4,6,8 및 더 많은 숫자로 나눌 수있는 가까운 이웃 인 72 를 선택합시다.

• time to double=72/rate

이는 72 의 규칙입니다! 쉬운 미풍.

경우에 당신을 찾고 싶어하는 시간을 배,다음을 사용할 수 있습니다 ln(3)~109.8 및 get

• 시간 트리플=110/율

는 또 다른 유용한 엄지손가락의 규칙. 72 의 규칙은 금리,인구 증가,박테리아 배양 및 기하 급수적으로 증가하는 모든 것에 유용합니다.

여기서 어디로 가야합니까?

자연 로그가 더 의미가 있기를 바랍니다—기하 급수적 인 성장의 양에 필요한 시간을 알려줍니다. 나는 그것을 고려”자기 때문에”전자가 보편적인 비율의 성장,그래서 ln 로 간주될 수 있는”보편적인”방법을 알아내는 방법을 오는 것을 성장합니다.

$\ln(x)$를 볼 때”x 로 성장할 시간”이라고 생각하십시오. 다음 기사에서 우리는 e 와 ln 을 함께 가져올 것이고,수학의 달콤한 향기가 공기를 채울 것입니다.

부록:E 의 자연 로그

빠른 퀴즈:$\ln(e)$는 무엇입니까?

• 수학 로봇은 다음과 같이 말합니다:역함수로 정의되기 때문에 분명히$\ln(e)=1$
• 직관적 인 인간: ln(e)은”e”성장 단위(약 2.718)를 얻는 데 걸리는 시간입니다. 그러나 e 는 1 단위 시간 이후의 성장량이므로$\ln(e)=1$입니다.

직관적으로 생각하십시오.

다른 글에서 이 시리즈

1. 는 직관적인 가이드하여 지수 함수&e
2. Demystifying 자연 로그(ln)
3. Visual 가이드 간단하고,화합물과 지속적인 관심 요금
4. 의 일반적인 정의 e(Colorized)
5. 이해가 지수(왜 0^0=1?)
6. 사용하여 로그에서 현실 세계
7. 는 방법을 생각으로 지수 및 대수
8. 이해 이산에 대한 지속적인 성장
9. 무엇 지수를 정말 의미합니까?
10. Q:왜 e 가 특별합니까? (2.718… 2,3.7 또는 다른 숫자가 아닌가?)