다른 섹션에서 언급되었다는 특성의 고체,액체 및 가스의 수를 차지했으면 우리 가정 물질의 원자나 분자가는 지속적으로 움직이고 있습니다. 보일의 법과 다른 가스의 법률에 지금 우리에게 훨씬 더 정량에 대한 정보 가스,그리고 그것은 가치가 있는지 여부를 묻는 이전 모델을 만들 수 있는 우리 정량 예측에서는 계약으로 이러한 법이 있습니다. 이 질문에 답하면서 우리는 또한 온도와 열 에너지의 본질에 대한 중요한 통찰력을 얻게 될 것입니다.

분자 운동에 기초한 가스 거동의 미세한 이론을 가스의 운동 이론이라고합니다. 그 기본 가정은 표 1 에 나열되어 있습니다:

표\(\PageIndex{1}\)가스의 운동 이론의 가정.

1 가스 내의 분자는 작고 매우 멀리 떨어져 있습니다. 가스가 차지하는 부피의 대부분은 빈 공간입니다.

2 개의 가스 분자는 일정한 무작위 운동에있다. 많은 분자가 다른 분자와 마찬가지로 한 방향으로 움직이고 있습니다.

3 분자는 서로 그리고 용기의 벽과 충돌 할 수 있습니다. 벽과의 충돌은 가스의 압력을 설명합니다.

4 충돌이 발생하면 분자는 운동 에너지를 잃지 않습니다. 총 운동 에너지의 모든 분자는 일정하게 유지 하지 않으면 일부 외부의 간섭으로.

5 분자 발휘 없는 매력적인 또는 반발에 힘을 다른 하나는 동안을 제외하고 프로세스의 충돌이 발생합니다. 충돌 사이에는 직선으로 움직입니다.

그들로부터 파생 가능 다음과 같은 표현한 가스의 압력을 측면에서의 특성을 분자:

\P,V=압력 및 양의 가스

N=숫자의 분자

m=대량의 각 분자

(u2)ave=평균(또는 말)의 사각형의 모든 개별적인 분자의 속도를 얻을 수 있습니다. 이 평균 속도해야 하기 때문에 사용 압력에 비례하는 사각형의 분자 속도,분자의 충돌을 일으킬 다른 분자 생산성을 발휘할 수 있습니다 다른 속도를 얻을 수 있습니다.

Eq 를 유도하는 절차에 대해 우리 자신에 관한 것보다. \(\ref{1}\),방정식을 검사하고 일반적인 기능이 우리가 기대하는만큼 많은 것을 보도록하겠습니다. 어떤면에서는 수식으로 이것을 할 수있는 능력이 그것을 도출하는 능력보다 더 유용합니다. 그림\(\PageIndex{1}\)

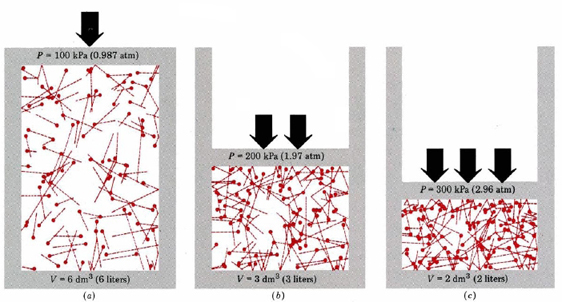첫째,방정식 저희에게 말하는 가스의 압력에 비례하여 분자의 수 나눈다. 이것은 다음과 같 그래픽으로서 그림\(\PageIndex{1}\),는 컴퓨터가 그려진 동일한 수의 가스 분자를 차지하는 각각의 세 가지 다른 볼륨입니다. “꼬리”에서 각 분자 보여줍니다 정확한 경로로는 분자전이크로초—상 빠른 분자가고 있었다. 꼬리 길이의 제곱의 평균은(u2)ave 에 비례하며 세 다이어그램 모두에서 동일합니다. 또한 모든 분자는 동일한 질량을 가지고 있다고 가정합니다.보시다시피,가스의 부피를 줄이면 컨테이너 벽의 단위 면적당 충돌 횟수가 증가합니다. 각 충돌은 벽에 힘을 발휘합니다;단위 면적당 힘은 압력이므로 단위 면적당 충돌 횟수는 압력에 비례합니다. 볼륨을 반으로 줄이면 보일의 법칙에 요약 된 실험 사실에 동의하는 예측 인 압력이 두 배가됩니다. 방정식\(\ref{1}\)는 또한 압력이 각 가스 분자의 질량에 비례한다고 말합니다. 다시 말하지만,이것은 우리가 기대하는 것입니다. 무거운 분자는 동일한 속도로 가벼운 분자보다 벽에 더 큰”푸시”(이것에 대한 기술적 용어는 충동 임)를줍니다.

마지막으로 방정식은 압력이 분자 속도의 제곱의 평균에 비례한다는 것을 알려줍니다. 이에 대한 의존도 광장의 속도는 합리적인 경우에 우리는 깨닫는 배속의 분자의 두 가지 효과.

첫째,분자는 주어진 시간 길이로 더 멀리 이동할 수 있으며 벽과의 충돌 횟수를 두 배로 늘릴 수 있습니다. 이것은 압력을 두 배로 늘릴 것입니다. 둘째,분자의 속도를 두 배로 늘리면 각 충돌의 푸시 또는 임펄스가 두 배가됩니다. 이렇게하면 압력이 다시 두 배가됩니다. 따라서 배로 분자의 속도 배로,압력 및 대한의 큰 숫자 분자,P 에 비례하는 평균 속도합니다.