보일의 법
Robert Boyle(1627-1691),영어 화학자이자,널리 중 하나가 될 것으로 간주의의 설립자는 현대적인 실험 과학의 화학. 그는이 발견되는 배의 압력을 밀폐된 가스 샘플을 유지하면서 그 온도를 일정하게 발생의 볼륨 가스를 절반으로 단축된다. 보일의 법에는 볼륨의 주어진 대량의 가스 반비례 압력 온도가 일정하게 유지. 이 방법으로 역 관계가 설명됩니다. 한 변수의 값이 증가함에 따라 다른 변수의 값이 감소합니다.
육체적으로,무슨 일이 일어나고 있습니까? 가스 분자는 움직이고 있으며 서로 일정한 거리를두고 있습니다. 압력의 증가는 분자를 서로 가깝게 밀어 넣어 부피를 감소시킵니다. 압력이 감소하는 경우에,가스는 더 큰 양에서 대략 움직이게 자유롭습니다.

수학적으로 보일의 법칙은 방정식으로 표현 될 수 있습니다:
\
\(k\)는 일정한 특정의 샘플 가스에 대량의 가스 온도. 아래 표는 일정한 온도에서 설정된 양의 가스에 대한 압력 및 부피 데이터를 보여줍니다. 세 번째 열은이 데이터에 대한 상수\(\left(k\right)\)의 값을 나타내며 항상 압력에 부피를 곱한 값과 같습니다. 변수 중 하나가 변경됨에 따라 다른 하나는\(P\times V\)의 곱이 항상 동일하게 유지되는 방식으로 변경됩니다. 이 특별한 경우,그 상수는\(500\:\text{atm}\cdot\text{mL}\)입니다.
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
데이터의 그래프에서 테이블에 추가 설명은 반비례 관계의 자연 보일의 율법(아래 그림 참조). 볼륨은\(x\)-축에 플롯되며\(y\)-축에 해당하는 압력이 있습니다.
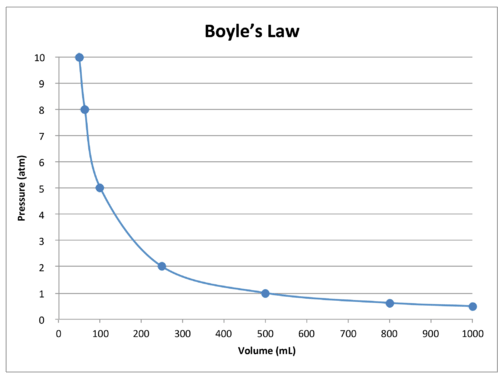
보일의 법칙은 가스에 대한 변화하는 조건을 비교하는 데 사용될 수 있습니다. 우리는\(P_1\)와\(V_1\)를 사용하여 가스의 초기 압력과 초기 부피를 나타냅니다. 변경이 이루어진 후\(P_2\)및\(V_2\)는 최종 압력 및 부피를 나타냅니다. 수학의 관계를 보일의 법률가:
\
이 방정식 계산하는 데 사용할 수 있는 하나의 네 가지 수량인 경우 다른 세 가지 알려져 있습니다.
예\(\PageIndex{1}\)
산소 가스 샘플의 부피는\(425 \: \text{mL}\)압력이\(387\:\text{kPa}\)와 같을 때. 가스는\(1.75\:\text{L}\)컨테이너로 확장 할 수 있습니다. 가스의 새로운 압력을 계산하십시오.
솔루션
1 단계:목록으로 알려진 수량을 계획하는 문제입니다.
알
- \(P_1=387\:\text{kPa}\)
- \(V_1=425\:\text{mL}\)
- \(V_2=1.75\:\text{L}=1750\:\text{mL}\)
알
- \(P_2=? \:\text{kPa}\)
알 수없는 압력\(\left(P_2\right)\)에 대해 해결하기 위해 보일의 법칙을 사용하십시오. 두 볼륨(\(V_1\)및\(V_2\))이 동일한 단위로 표현되므로\(V_2\)가\(\text{mL}\)로 변환되는 것이 중요합니다.
2 단계:해결.
먼저\(P_2\)에 대해 풀기 위해 방정식을 대수적으로 재정렬하십시오.
\
자 대리 알려진 수량 방정식으로는 해결합니다.나는 당신이 그것을 할 수 있다고 생각하지 않지만,나는 그것을 할 수 있다고 생각하지 않는다.
볼륨이 원래 값의 4 배를 약간 넘도록 증가하여 압력이 약 4 분의 1 로 감소합니다. 압력은\(\text{kPa}\)에 있으며 값은 세 가지 중요한 수치입니다. 문제 전반에 걸쳐 일관된 한 모든 압력 또는 부피 단위를 사용할 수 있습니다.