원자 Orbitals

궤도는 양자 역학적의 구체화하는 단점이 있다. 달리,그 개념의 간단한 원형으로 궤도 고정 radius,궤도 있는 수학적으로 파생 된 지역의 공간으로 다른의 가능성을 갖는 전자현.

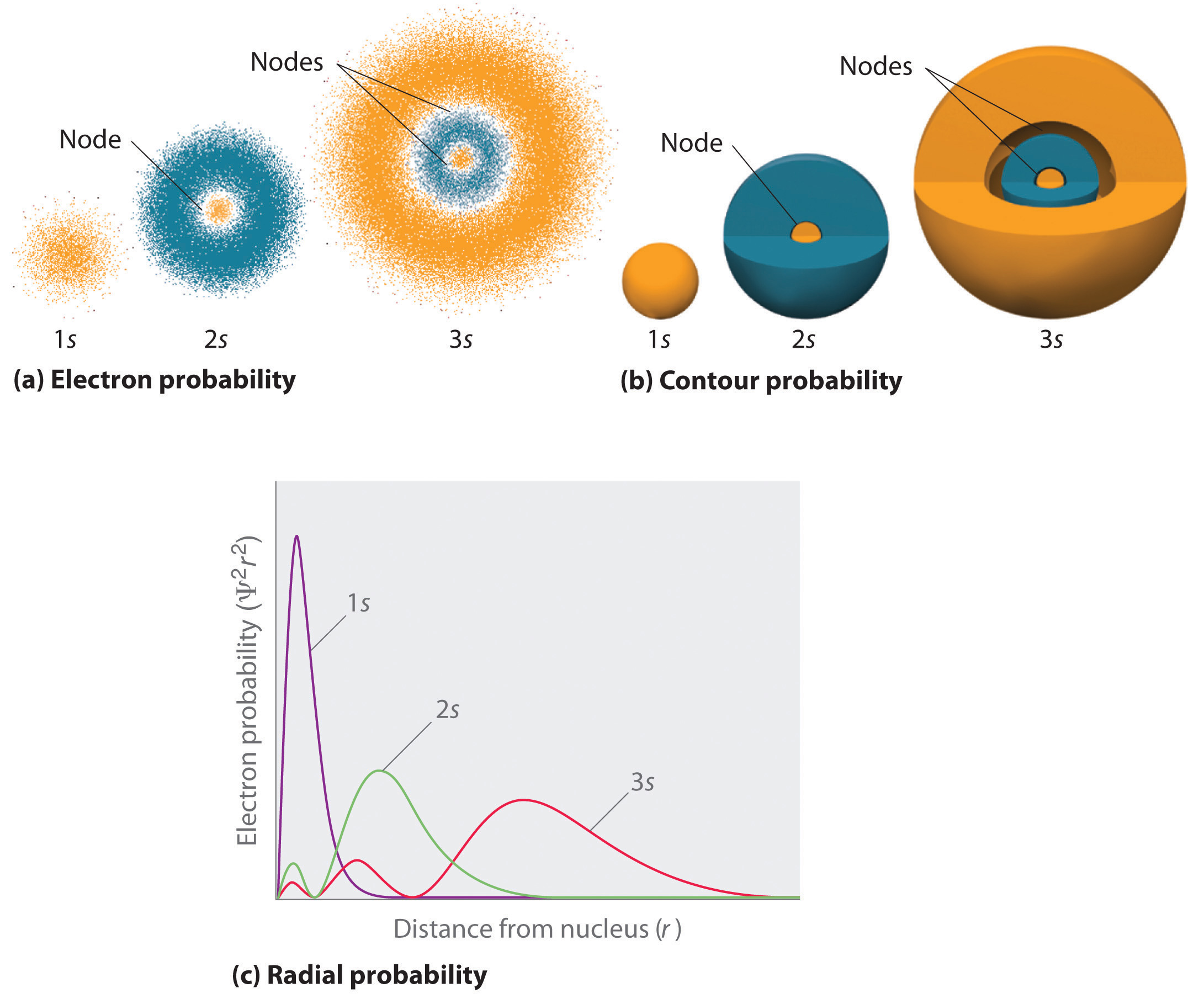
전자 확률 분포를 나타내는 한 가지 방법은 수소의 1s 궤도에 대해 그림 6.5.2 에 도시되었다. 기 때문에 Ψ2 의 가능성을 제공합을 찾기 전에 주어진 공간의 볼륨(과 같이 입방 pico meter),의 음모 Ψ2 대 거리에서 핵(r)은 음모의 확률 밀도입니다. 1s 궤도는 구형 적으로 대칭이므로 주어진 지점에서 1s 전자를 발견 할 확률은 핵과의 거리에만 의존합니다. 확률 밀도는 r=0(핵에서)에서 가장 크며 거리가 증가함에 따라 꾸준히 감소합니다. R 의 매우 큰 값에서 전자 확률 밀도는 매우 작지만 0 은 아닙니다.

반대로 우리가 계산할 수 있습니다 원형 확률(확률을 찾는 1s 전자 거리에 r 에서 핵)추가하여 함께 가능성의 전자에 있는 모든 지점에서의 시리즈 x 둥근의 껍질을 반경 r1,r2,r3,…,rx−1,rx. 에서 효과,우리는 나누어 원자로 아주 얇은 동심 조개와 같은 많은 층의 양파(일(a)그림\(\PageIndex{1}\)),및 계산을 찾는 확률 전자에서 각 구형 쉘입니다. 을 기억하는 전자 확률 밀도에서 가장 큰 r=0(부분(b)그림\(\PageIndex{1}\)),그래서 그 밀도는 점이 가장 큰 위해 가장 작은 둥근 껍질 부분에서(a)그림\(\PageIndex{1}\). 대조적으로,각 구형 쉘의 표면적은 4nr2 와 같으며,이는 그림\(\PageIndex{1}\)에서 r(part(c))이 증가함에 따라 매우 빠르게 증가합니다. 기 때문에 표면적의 둥근 포탄을 증가는 더 급속하게 증가와 함께 r 보다 전자 확률 밀도가 감소하면,줄거리의 레이디얼 확률을 최대에서는 특정 거리(part(d)그림\(\PageIndex{1}\)). 가장 중요한 때,r,매우 작은 표면적의 둥근 포탄은 그래서 작은 총 찾을 가능성 전자가 가까이 핵은 아주 낮에는 핵,전자는 확률이 없어진다(부분(d)그림\(\PageIndex{1}\)).

에 대한 수소 원자,피크에서는 방사형 확률에서 발생합 r=0.529Å(52.9 동)는 정확하게 반경을 계산한 단점에 대한 n=1 궤도. 따라서 양자 역학에서 얻은 가장 가능성있는 반경은 고전 역학에 의해 계산 된 반경과 동일합니다. 에서 보어의 모델,그러나 전이었다으로 간주되 이 거리에는 100%시간의 반면,양자 기계적인 슈뢰딩거는 모델,그것이 거리에서만 일부 시간이다. 두 모델의 차이는 전자의 웨이블리크 거동과 하이젠 베르그 불확실성 원리에 기인한다.

그림\(\PageIndex{2}\)는 수소 1s,2s 및 3s 오비탈에 대한 전자 확률 밀도를 비교합니다. 세 가지 모두 구형 대칭입니다. 에 대해 2 및 3orbitals,그러나(다른 모든 s 궤도뿐만 아니라),전자 확률 밀도가 떨어지지 않을 원활하게 증가와 함께 r. 대신,시리즈의 minima and maxima 는 관찰에서 반경 방향 확률(부분(c)그림\(\PageIndex{2}\)). 의 최소값에 해당하는 둥근 노드(지역의 영 전자 확률)를 대체와 둥근 지역의 아닌 전자는 확률입니다.