Purplemath
수학에서는”id”방정식이는 항상 진실하다. 이들은 직각 삼각형에 대한 피타고라스 정리의”a2+b2=c2″와 같이”x=x”와 같이”사소하게”true 일 수도 있고 유용하게 true 일 수도 있습니다. 삼각 정체성의 부하가 있지만,다음은 당신이보고 사용할 가능성이 가장 높은 것들입니다.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

기본적이고 피타고라스의 신원
제휴
방법을 통 a”co-(뭔가)”삼각 비율은 항상 역의 일부는”비 co”비율이 있습니다. 이 사실을 사용하여 cosecant 가 사인과 함께 가고 secant 가 코사인과 함께 간다는 것을 똑바로 유지하는 데 도움이 될 수 있습니다.
다음(특히 아래 세 가지 중 첫 번째)을”피타고라스”정체성이라고합니다.
sin2(t)+cos2(t)=1
tan2(t)+1=sec2(t)
1+cot2(t)=csc2(t)
광고
참고는 세 id 위의 모든를 포함 및 제곱 번호는 1 입니다. 당신이 볼 수있는 피타고라스-Thereom 관계를 명확하게 고려하는 경우 단,어디에 각 t,”반대”측은 죄(t)=y”인접한”측은 cos(t)=x,빗변은 1 입니다.
우리는 추가적인 정체성과 관련된 기능의 상태를 트리거 비율:
sin(t)=–sin(t)
cos(t)=cos(t)
tan(t)=–탄(t)
통지에서는 특정 사인 및 접는 이상한 기능 는 대칭 기원에 대한하는 동안,코사인도 함수는 대칭 y-axis. 할 수 있다는 사실을 인수””마이너스 등록 외부의(사인 및 접)이거나 그것은 전적으로(예 코사인)사용할 때 도움이 될 수 있습니다 복잡한 표현입니다.
각도계와 차이점 신원
sin(α+β)=sin(α)cos(β)+cos(α)sin(β)
sin(α–β)=sin(α)cos(β)cos(α)sin(β)
cos(α+β)=cos(α) cos(β)–sin(α)sin(β)
cos(α–β)=cos(α)cos(β)+sin(α)sin(β)
방법에 의해 상기 정체성,각도로 표시하여 그리스어 문자입니다. A 형 문자 인”α”는”alpha”라고 불리며”AL-fuh”라고 발음됩니다. B 형 문자 인”β”는”bay-tuh”로 발음되는”beta”라고합니다.
콘텐츠를 계속 아래
더블 각 Id
sin(2x)=2sin(x)cos(x)
cos(2x)=cos2(x)–sin2(x)=1–2sin2(x)=2cos2(x) –1
반 각 Id
위의 정체성을 다시 할 수 있습니다-에 의해 명시된 제곱 각 측면과 두배로 하는 모든 의 각도를 측정합니다. 결과는 다음과 같습니다:
Affiliate

Sum Identities
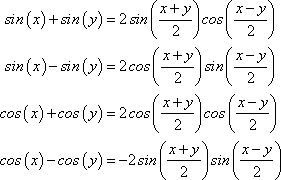
Product Identities
제휴
할 것을 사용하여 모든 이들의 정체성,또는 거의 그래서,증명에 대한 다른 trig 정체성과 해결하기 위한 삼각 답변을 받으실 수 있습니다. 그러나 만약 당신이 공부하는 미적분,특히 주의하여 다시 사인과 코사인 반 각도가 정체성이 될 것이기 때문에 그들을 사용하여 많은에서 필수적인 수학.
URL: 나는 이것이 어떻게 작동하는지 이해하지 못한다.