関連ページ
セットの詳細レッスン
二つのセットの交点
三つのセットの交点
次の図は、セット、互いに素なセット、サブセット、交差点とセットの和集合の補数のためのセット操作とベン図を示しています。 より多くの例と解決策については、ページを下にスクロールします。
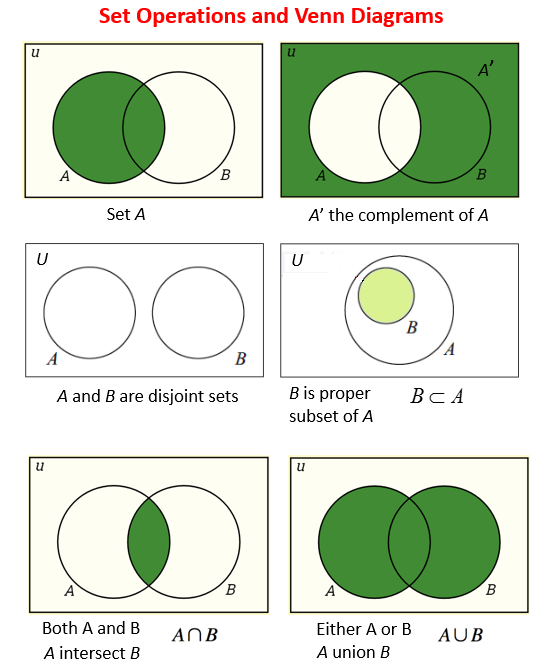
考慮されているすべての要素のセットは、ユニバーサルセット(U)と呼ばれ、arectangleで表されます。a’={x|x∈U and x∈A}
- 集合Aの補集合A’は、Uの要素の集合ですが、これは、BがAの部分集合であるが、B⊆Aであることを意味する。
- AとBの共通部分は、集合Aと集合Bの両方の元の集合である。
- A∩B={x|x∈Aとx∈B}
- euのAおよびBの要素を設定またはセットB∪B={x|x∈A x∈B}
- ∩∅=∅
- ∪∅=A
- ビデオレッスン
セット操作やVenn図
例:
1. セット間の関係を示すベン図を作成します。
Uは1から15までの整数の集合です。
Aは3の倍数の集合です。
bは素数の集合です。
Cは奇数の集合です。
2. 次のベン図を考えると、次のセットのそれぞれを決定します。
A)A≤B
b)A≤B
c)(A≤B)’
d)A’≤B
e)A≤B’
- ビデオレッスンを表示
例:
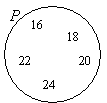
与えられたセットPは15と25の間の偶数のセットです。 ベン図を描画してラベルを付けて、集合Pを表し、ベン図内の集合Pのすべての要素を示します。
解決策:
Pの要素をリストします。
P= {16, 18, 20, 22, 24} ← ”の間には15と25が含まれていません
円または楕円を描きます。 要素をPに入れます。
例:
セットを表すためにベン図を描画し、ラベルを付けます
R={月曜日、火曜日、水曜日}。
ソリューション:
円または楕円を描きます。 Rというラベルを付けています。 要素をRに入れます。

例:セットQ={x:2x–3<11を考えると、xは正の整数です}。 ベン図を描いてラベルを付けて集合Qを表す。
解:
方程式が与えられているので、最初にxを解く必要があります。
2x–3<11⇒2x<14⇒x<7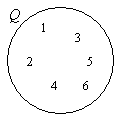
だから、Q= {1, 2, 3, 4, 5, 6}
円または楕円を描く。 Qにラベルを付けます。
要素をQに入れます。
ベン図ビデオ
ベン図とは何ですか?
- ビデオレッスンを表示
ベン図-二つのサブセット
二つのサブセットを持つベン図について学びます。
- ビデオレッスンを表示
ベン図-リージョンを使用して二つのサブセット
リージョンを使用して二つのサブセットを持つベン図につ
- ビデオレッスンを表示
三つのサブセットを持つベン図
三つのサブセットを持つベン図について学びます。
- ビデオレッスンを表示
様々な数学のトピックを練習するために、以下の無料のMathway電卓と問題ソルバーを試してみてください。 与えられた例を試してみるか、あなた自身の問題を入力し、ステップバイステップの説明であなたの答えを確認してください。 