Questa sezione copre:
- Introduzione alle Funzioni a Tratti
- la Valutazione di Funzioni a Tratti
- Grafica a Tratti Funzioni
- Come capire se un Piecewise Funzione è Continua o Non Continua
- Ottenere le Equazioni di Tratti Grafici di funzioni
- Assoluto Valore come Piecewise Function
- Trasformazioni di Funzioni a Tratti
- Piecewise Function Problemi di Word
- Pratica

funzioni a Tratti (o pezzo-saggio funzioni) sono quello che sono chiamato: pezzi di diverse funzioni (sotto-funzioni) tutto su un grafico. Il modo più semplice per pensarli è se hai disegnato più di una funzione su un grafico e hai appena cancellato parti delle funzioni in cui non dovrebbero essere (lungo le \(x\)); sono definite in modo diverso per diversi intervalli di \(x\). \(y\) è definito in modo diverso per diversi valori di \(x\); usiamo \(x\) per cercare in quale intervallo si trova, in modo da poter scoprire cosa dovrebbe essere \(y\).
Si noti che c’è un esempio di inverso di una funzione a tratti qui nella sezione Inverses of Functions.
Here’s an example and graph:
|
Piecewise Function |
Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Ci sono altri modi per visualizzarlo, come usare un “for” invece di un “if” e usare virgole o punti e virgola invece di “if”.) Dominio: \ (\mathbb {R},\,\,\,\text {or}\,\, \ left ({- \infty, \infty}\right)\) Intervallo: \(\mathbb{R},\,\,\,\text{o}\,\,\left( {-\infty ,\infty } \right)\) |
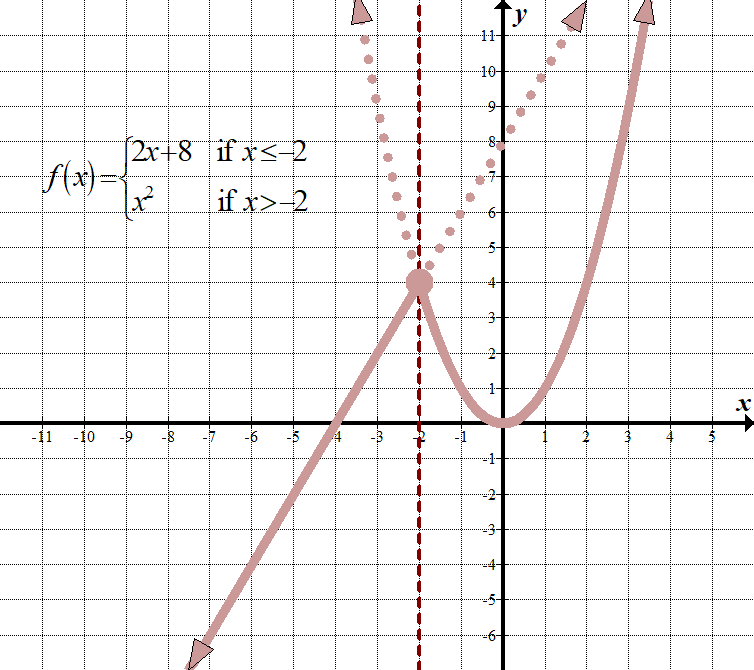 |
che Cosa questo significa è che per ogni \(x\) inferiore o uguale a -2, abbiamo bisogno di un grafico con la linea di \(2x+8\), come se fosse l’unica funzione del grafico. Per ogni valore\ (x\) maggiore di -2, abbiamo bisogno di graph \({{x} ^ {2}}\), come se fosse l’unica funzione sul grafico. Quindi dobbiamo “sbarazzarci” delle parti che non ci servono. Ricorda che usiamo ancora l’origine come punto di riferimento per entrambi i grafici!
Vedere come la linea verticale \(x=-2\) agisce come una linea di “confine” tra i due grafici?
Si noti che il punto \((-2,4)\) ha un cerchio chiuso su di esso. Tecnicamente, dovrebbe appartenere solo alla funzione \(2x+8\), poiché quella funzione ha il segno minore o uguale, ma poiché il punto è anche sul grafico \({{x}^{2}}\), possiamo semplicemente usare un cerchio chiuso come se appaia su entrambe le funzioni. Vedi, non cosi ‘ male, vero?
Valutazione delle funzioni a tratti
A volte, ti verranno fornite funzioni a tratti e ti verrà chiesto di valutarle; in altre parole, trova i valori \(y\) quando ti viene dato un valore\ (x\). Facciamo questo per \(x = -6\) e \(x = 4\) (senza usare il grafico). Ecco di nuovo la funzione:
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ se }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ se }x>-2\end{align} \right.\)
Vogliamo prima guardare le condizioni a destra, per vedere dove si trova il nostro \(x\). Quando \(x = -6\), sappiamo che è inferiore a -2, quindi colleghiamo solo il nostro \(x\) a \(2x+8\). \(f (x)\) o\ (y\) è \((2)(-6)+8=-4\). Non ci interessa nemmeno il \ (\boldsymbol {{x}^{2}}\)! E ‘cosi’ facile. Puoi anche vedere che lo abbiamo fatto correttamente usando il grafico sopra.
Ora prova \(x = 4\). Guardiamo prima a destra e vediamo che il nostro \(x\) è maggiore di -2, quindi lo colleghiamo a \({{x}^{2}}\). (Possiamo semplicemente ignorare il \(2x+8\) questa volta.) \(f(x)\) o \(y\) è \({{4}^{2}}=16\).
Rappresentare graficamente le funzioni a tratti
Probabilmente ti verrà chiesto di rappresentare graficamente le funzioni a tratti. A volte i grafici conterranno funzioni che non sono continue o discontinue, il che significa che devi prendere la matita al centro del grafico quando lo stai disegnando (come un salto!). Funzioni continue significa che non devi mai prendere la matita se si dovesse disegnare da sinistra a destra.
E ricorda che i grafici sono funzioni vere solo se superano il test della linea verticale.
Disegniamo queste funzioni a tratti e determiniamo se sono continue o non continue. Nota come disegniamo ogni funzione come se fosse l’unica, quindi “cancelliamo” le parti che non sono necessarie. Otterremo anche il Dominio e l’intervallo come abbiamo fatto qui nella sezione Funzioni algebriche.
| Piecewise Function | Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\) |
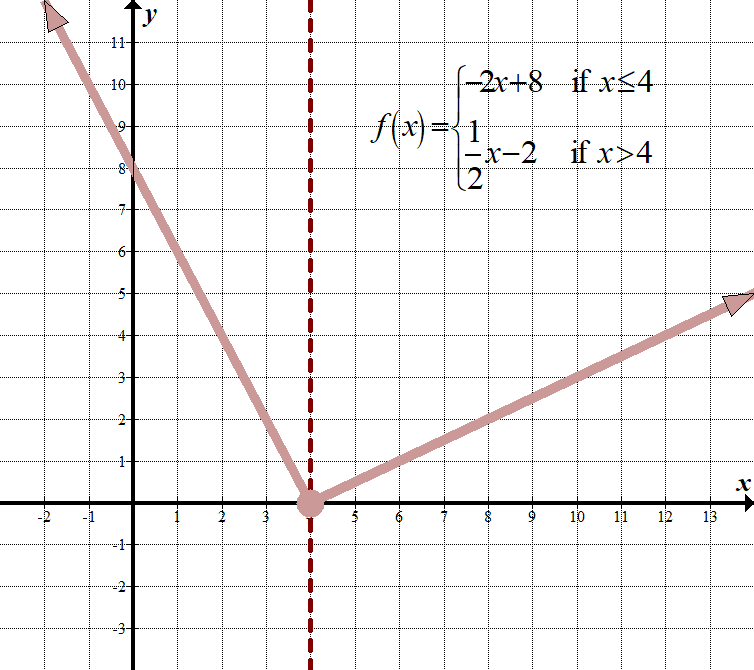 |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) |
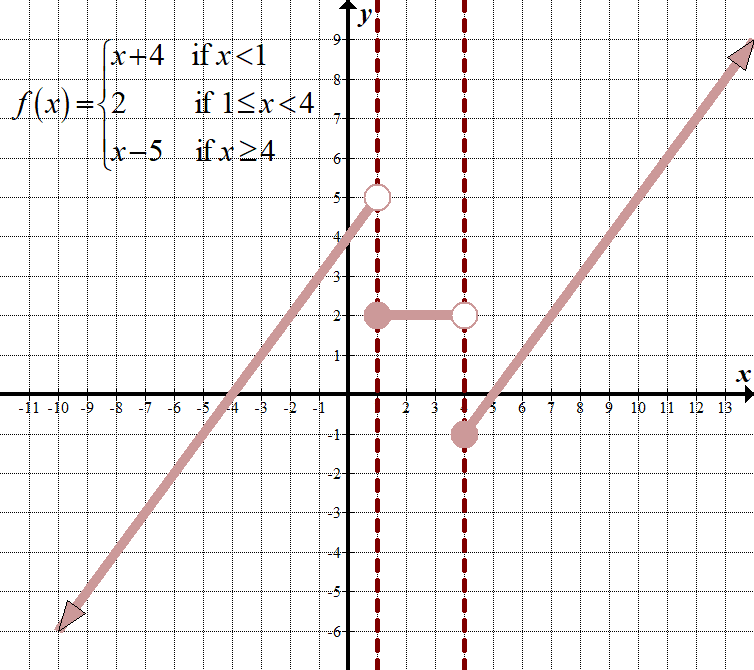 |
We can actually put piecewise functions in the graphing calculator:
| Piecewise Function Screens | Steps and Notes |
| Enter the piecewise function on three lines:
Ecco il grafico:
|
Per mettere piecewise function \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{se }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se 1 }\le x<4\\-5+x\,\,\,\,\,\text{se }x\ge 4\end{array} \right.\ ) nella calcolatrice, è possibile inserire la funzione su tre righe dividendo la funzione in ogni intervallo da una “disuguaglianza di prova” di quell’intervallo (e guarda le parentesi!).
Il motivo per cui dividiamo per gli intervalli o le disuguaglianze è perché la calcolatrice restituirà un 1 se la disuguaglianza (come \(x<1\)) è vera; ad esempio, \((x+4)\) finirà solo per \((x+4)/(1)\) quando \(x<1\). Quando \(x \ ge 1\), stiamo dividendo per 0, quindi non verrà disegnato nulla. Ecco cosa possiamo mettere nella calcolatrice: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {x+4} \right)/\left( {x<1} \right)\\{{Y}_{2}}=\left( 2 \right)/\left( {x\ge 1\text{ e }x<4} \right)\\{{Y}_{3}}=\left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (si noti che è anche possibile inserire questa riga moltiplicando le condizioni invece che dividere, e l’utilizzo di segni più tra ciascuna delle tre funzioni/intervalli di: \(\displaystyle {{Y}_{1}}=\left( {x+4} \right)\left( {x<1} \right)+\left( 2 \right)\left( {x\ge 1\text{ e }x<4} \right)+\left( {-5+x} \right)\left( {x\ge 4} \right)\).) Ecco le sequenze di tasti per l’utilizzo di tre righe. Si noti che si utilizza 2nd MATH (TEST) per arrivare alla schermata che ha il \(\le\), \(\ge\), e così via. Ad esempio, 2nd MATH 6 ti ottiene \(\le \). Usa 2nd MATH (TEST), right to LOGIC, quindi 1, per “and” in \({{Y}_{2}}\).
|
Come capire se a Tratti Funzione è Continua o Non Continua
Per stabilire se si tratti grafico è continuo o non continuo, è possibile guardare i punti di contorno e vedere se \(y\) il punto è lo stesso per ciascuno di loro. (Se i \(y\) fossero diversi, ci sarebbe un “salto” nel grafico!)
Proviamo questo per le funzioni che abbiamo usato sopra:
| Piecewise Function | Check Boundary Points |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) | Let’s check \(x=4\) in both parts of the function, since 4 is the “boundary point”:
\(\begin{array} {l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end {array}\) Poiché \(0=0\), questa funzione a tratti è continua. |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se 1 }\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\text{se }x\ge 4\end{array} \right.\) | Controlliamo le prime due parti della funzione. Nota nella seconda parte, \(y\) è sempre 2:
\(\begin{array} {l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end {array}\) Poiché \(5\ne 2\), possiamo fermarci qui e notare che questa funzione a tratti non è continua. Se i \(y\) fossero uguali, dovremmo andare uno per controllare il punto di confine successivo a \(x=4\). |
Ottenere equazioni da grafici di funzioni a tratti
Potrebbe essere richiesto di scrivere una funzione a tratti, dato un grafico. Ora che sappiamo cosa sono le funzioni a tratti, non è poi così male!
Per esaminare come ottenere equazioni da grafici lineari, vedi Ottenere le equazioni di una retta e dalla quadratica, vedi Trovare un’equazione quadratica da punti o da un grafico.
Ecco i grafici, con spiegazioni su come derivare le loro equazioni a tratti:
| Piecewise Function Graph | Procedure to get Function |
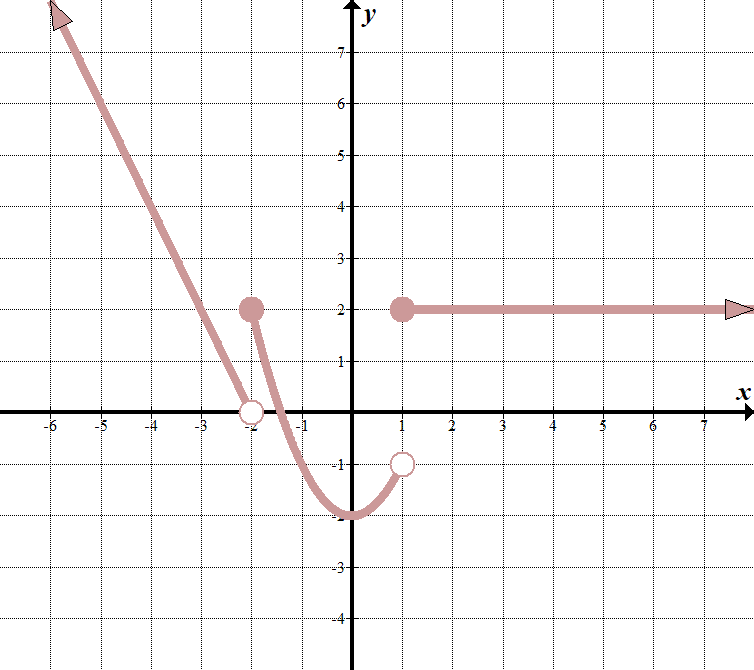 |
We see that our “boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints):
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\text{se }x<-2\\\text{ }……\,\,\,\,\,\,\,\,\text{se }-\text{2 }\le x<1\\\text{ }……\,\,\,\,\,\,\,\,\text{se }x\ge 1\end{array} \right.\) Possiamo scegliere due punti\ ((-2,0)\) e\ ((-3,2)\) sulla linea più a sinistra per ottenere l’equazione\(y=-2x-4\). La funzione centrale è \(y = {{x}^{2}}-2\), e la funzione più a destra è solo la linea orizzontale \(y = 2\). Quindi, la funzione a tratti è: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x-4\,\,\,\,\,\,\,\text{se }x<-2\\\text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{se }-\text{2}\le x<1\\\text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }x\ge 1\end{array} \right.\) |
 |
Vediamo che la nostra “linea di confine” è a \(x=5\). Poiché le linee si incontrano a \((5,4)\), non importa dove mettiamo il segno \(\le \) o \(\ge \) ; non possiamo metterlo in entrambi i posti, o non sarebbe una funzione. Abbiamo finora:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{se }x<5\\\text{ }……\,\,\,\,\,\,\,\,\,\text{se }x\ge 5\end{array} \right.\) Ancora una volta, dobbiamo guardare ogni riga separatamente per determinare le loro equazioni. Possiamo prendere 2 punti da ogni linea per ottenerli, o derivare da pendenze e\(y\)–intercetta; la funzione a tratti è: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\text{se }x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\text{se }x\ge 5\end{array} \right.\) |
Valore assoluto come funzione a tratti
Possiamo scrivere funzioni a valori assoluti come funzioni a tratti – è davvero bello! Si potrebbe desiderare di rivedere Risolvere equazioni di valore assoluto e disuguaglianze prima di continuare a questo argomento.
Diciamo che abbiamo la funzione \(f \ left (x \right)= \ left / x \ right/\). Da quello che abbiamo imparato in precedenza, sappiamo che quando \(x\) è positivo, dal momento che stiamo prendendo il valore assoluto, sarà ancora solo \(x\). Ma quando \(x\) è negativo, quando prendiamo il valore assoluto, dobbiamo prendere il contrario (negarlo), poiché il valore assoluto deve essere positivo. Ha senso? Quindi, per esempio, se avessimo \(|5|\), prendiamo solo ciò che è dentro il segno assoluto, poiché è positivo. Ma per \(/-5/\), dobbiamo prendere l’opposto (negativo) di ciò che è all’interno del valore assoluto per renderlo \(\displaystyle 5\,\,\,(-\,-5=5)\).
Questo significa che possiamo scrivere questa funzione di valore assoluto come una funzione a tratti. Si noti che possiamo ottenere il “punto di svolta” o “punto di confine” impostando qualsiasi cosa sia all’interno del valore assoluto su 0. Quindi useremo la funzione originale o negheremo la funzione, a seconda del segno della funzione (senza il valore assoluto) in quell’intervallo.
Per esempio, possiamo scrivere \(\displaystyle \left| x \right|\text{ }=\left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\text{se }x\ge 0\\-x\,\,\,\,\,\text{se }x<0\end{array} \right.\). Si noti inoltre che, se la funzione è continua (non c’è “salto”) nel punto di confine, non importa dove mettiamo i segni “minore o uguale a” (o “maggiore o uguale a”), purché non li ripetiamo! Non possiamo ripeterli perché, teoricamente, non possiamo avere due valori di \(y\) per lo stesso \(x\), o non avremmo una funzione.
Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):
| Absolute Value Function | Method to get Piecewise Function |
| \(g\left( x \right)=\left| {2x+3} \right|\) | Let’s first find the “boundary line”. Lo facciamo impostando ciò che è all’interno del valore assoluto su 0 e quindi risolvendo per \(\boldsymbol{x}\).
Quando \(2x + 3 \ ge 0\), otteniamo \(\displaystyle x \ ge – \ frac{3}{2}\) (in realtà, possiamo mantenere il \(\ge\) quando risolviamo). Quando \(2x + 3\) è positivo, lo prendiamo semplicemente “così com’è”, ma se è negativo, dobbiamo negare il tutto. Pertanto, la funzione a tratti è: \(\displaystyle \left| {2x+3} \right|=\left\{ \begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{se }x\ge\frac{3}{2}\text{ }\\-2x-3\,\,\,\,\,\text{se }x<\frac{3}{2}\end{array} \right.\) Provalo-funziona! |
| \(f\left( x \right)=\left|{{{x}^{2}}-4} \right/\) | Troviamo prima le “boundary line(s)”; impostiamo ciò che è all’interno del valore assoluto su 0.
Quando \({{x}^{2}}-4\ge 0\), otteniamo \(x \ le -2\) o \(x \ ge 2\) (prova alcuni numeri!). Quando \({{x}^{2}} -4\) è positivo, lo prendiamo semplicemente “così com’è”, ma se è negativo, dobbiamo negarlo. piecewise function: \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\text{se }x\le -2\\4-{{x}^{2}}\,\,\,\,\,\text{se }-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\text{se }x\ge 2\text{ }\end{array} \right.\) o \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\text{se }x\le -2\text{ }\,\,\text{o}\,\,\text{ }x\ge 2\\4-{{x}^{2}}\,\,\,\,\,\,\,\text{se }-2<x<2\end{array} \right.\) Di nuovo (poiché la funzione è continua), non importa dove abbiamo \(\le \) e \(\ge \) (al contrario di \(<\) e \(>\)), purché non li ripetiamo. |
| \(f\left( x \right)=2x+\left|{x+2} \right/\) | Questo è un po ‘ più complicato, dato che abbiamo un \(x\) dentro e fuori il valore assoluto. Per la “linea di confine”, usiamo solo ciò che è all’interno del valore assoluto.
Quando \(x + 2 \ ge 0\), otteniamo \(x\ge -2\). Ma per la funzione a tratti, dobbiamo usare l’intera funzione, inclusa la parte che è al di fuori del valore assoluto. Quindi, la funzione a tratti è: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}2x+x+2\,\,\,\,\,\text{se }x\ge -2\\2x-x-2\,\,\,\,\,\text{se }x<-2\end{array} \right.\) proviamo a semplificare: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\text{se }x\ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\text{se }x<-2\end{array} \right.\ ) Prova alcuni valori inferiori e grandi quindi -2; dovrebbero funzionare! |
| \(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\) | Questo è il più risolto con un segno grafico, dal momento che abbiamo un quadratica e abbiamo bisogno di sapere dove la funzione è positiva e negativa.
Innanzitutto, fattore il quadratico all’interno della funzione del valore assoluto su \(\left( {x-5} \right)\left( {x+1} \right)\). Quindi usa un grafico dei segni per vedere dove i fattori sono positivi e negativi, e ricorda che dove i fattori sono positivi, usiamo la funzione “così com’è”, e dove i fattori sono negativi, neghiamo la funzione: \(\displaystyle \left| {{{x}^{2}}-4x-5} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }x\le -1\,\,\,\,\text{o}\,\,\,\,x\ge 5\\-\left( {{{x}^{2}}-4x-5} \right)\,\,\,\,\text{se }-1<x<5\text{ }\end{array} \right.\) |
| \(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\) | Questa è una funzione razionale, dal momento che esiste una variabile nel denominatore.
Quando \(x + 2 \ ge 0\), otteniamo \(\displaystyle x\ge -2\). Quando \(x+2\) è positivo, basta prendere “così com’è”, ma se è negativo, dobbiamo negare che in valore assoluto): \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}\frac{{x+2}}{{x+2}}\,\,\,\,\,\,\,\,\,\text{se }x\ge -2\\\frac {{x-2}}{{x+2}}\,\,\,\,\,\,\text{se }x<-2\end{array} \right.\). Ma dobbiamo stare attenti, poiché \(x\ne 2\) (restrizione del dominio: il denominatore sarebbe 0). Pertanto, la funzione a tratti è: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\text{se }x>-2\\-1\,\,\,\,\,\,\text{se }x<-2\end{array} \right.\). |
Si può anche essere chiesto di prendere un valore assoluto grafico e scriverlo come una funzione a tratti:
| Absolute Value Graph | Method to get Piecewise Function |
 |
We see that our “boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Questo perché per ottenere la linea di confine con una funzione di valore assoluto, impostiamo ciò che è all’interno del valore assoluto su 0 e risolviamo per \(x\)).
Quando \(x > 0\), possiamo vedere che l’equazione della linea è \(y=2x-2\). Quando \(x < 0\), l’equazione è \(y=2x-2\). Siamo in grado di scrivere questo come un piecewise function: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\text{se }x>0\\-2x-2\,\,\,\text{se }x\le 0\end{array} \right.\) Possiamo anche scrivere questo come una funzione di valore assoluto trasformata: \(y=2\left|x \right| -2\) o \(y=\left|{2x} \right| -2\) (poiché 2 è positivo, può essere all’interno o all’esterno del \(\left|{ \ ,\,} \right/\)). (Questo ha senso poiché quando ciò che è dentro \(\left| {\,\,} \right|\) è \(> 0\), usiamo la funzione regolare \(y=2x-2\), e quando ciò che è dentro è \(< 0\), neghiamo la parte del valore assoluto per renderla \(y=-\left( {2x} \destra)-2\)). |
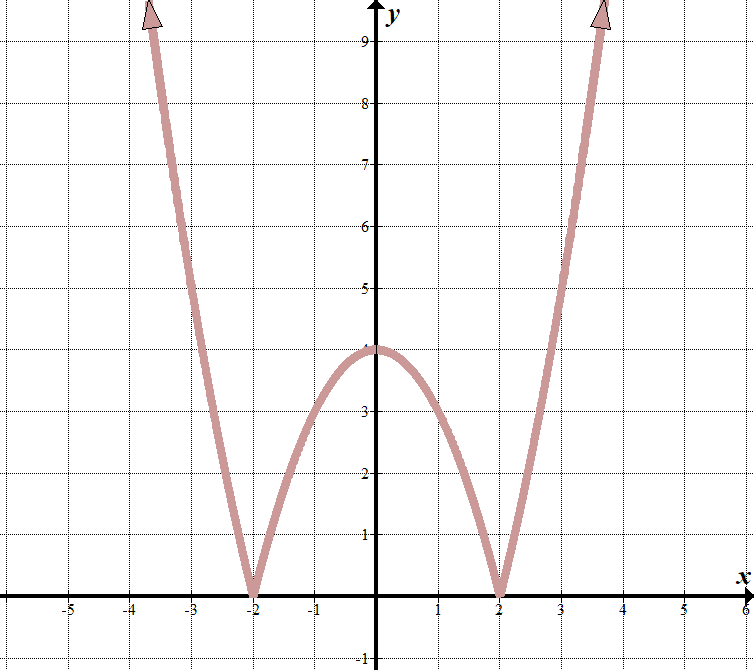 |
vediamo che il nostro “linee di confine” sono in \(x=2\) e \(x=-2\), quindi cosa c’è dentro il valore assoluto segno deve avere fattori di \(x-2\) e \(x+2\).
Quando \(x < -2\) o \(x > 2\), possiamo vedere che il grafico appare come la parte normale del grafico \(y = {{x}^{2}}-4\). (L’ho capito conoscendo i fattori e facendo una buona ipotesi!) Quando \(-2 < x <2\), l’equazione viene capovolta o negata (capovolta sull’asse \(x\)). Siamo in grado di scrivere questo come un piecewise function: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{se }x<-2\text{ o }x>2\\-{{x}^{2}}\text{+ 4}\,\,\,\,\,\,\text{se }-2\le x\le 2\end{array} \right.\) Possiamo vedere che questo ha iniziato una funzione quadratica trasformata \(y={{x}^{2}}-4\) con un valore assoluto attorno ad essa, poiché tutti i valori \(y\) sono positivi: \(y=\left| {{{x}^{2}}-4} \right|\). |
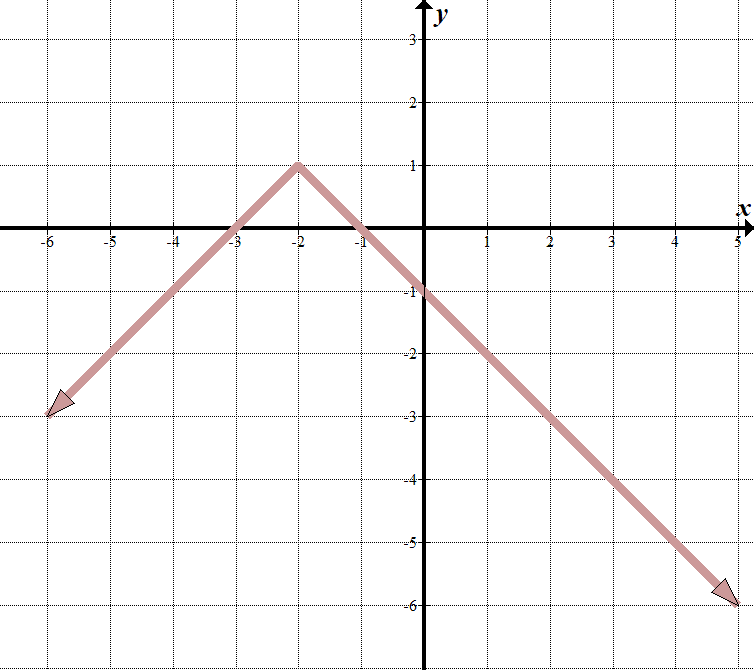 |
Vediamo che la nostra “linea di confine” è a \(x=-2\), quindi ciò che è dentro il segno del valore assoluto deve essere \(x+2\).
Quando \(x > -2\), possiamo vedere che l’equazione della linea è \(y=-x-1\). Quando \(x < -2\), la linea è \(y=x+3\). Siamo in grado di scrivere questo come un piecewise function: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-x-1\,\,\,\,\,\,\text{se }x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\text{se }x\le -2\end{array} \right.\) È probabilmente più facile scriverlo come una funzione di valore assoluto trasformata. Possiamo vedere che la funzione del valore assoluto genitore viene capovolta verticalmente, spostata a sinistra 2 e su 1. La nostra equazione del valore assoluto è \(y= – \ left / {x + 2} \ right|\,\,+\,\,1\). Questo è lo stesso della funzione a tratti sopra. Provalo-funziona! |
Trasformazioni di funzioni a tratti
Facciamo una trasformazione di una funzione a tratti. Abbiamo imparato a conoscere le funzioni padre e le loro trasformazioni qui nella sezione Grafici e trasformazioni padre. Probabilmente vorrai leggere prima questa sezione, prima di provare una trasformazione a tratti.
Trasformiamo la seguente funzione a tratti ruotata attorno all’asse \(x\), allungata verticalmente di un fattore di 2 unità, 1 unità a destra e 3 unità in alto.
Ci trarre \(-2f\left( x-1 \right)+3\), dove:
\(\displaystyle f\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\text{ se }x<&\text{ se 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ se }x\ge 4\end{align} \right.\)
Facciamo in modo di utilizzare i punti “confine” quando riempiamo il t-chart per la trasformazione. Ricorda che le trasformazioni all’interno delle parentesi sono fatte su \(x\) (facendo la matematica opposta) e all’esterno sono fatte su \(y\). Per creare un grafico a t, come mostrato nella tabella seguente, possiamo utilizzare i punti chiave, inclusi due punti su ciascuna delle “linee di confine”.
Nota che poiché questa trasformazione è complicata, possiamo trovare una nuova funzione a tratti trasformando i 3 “pezzi” e anche trasformando i “\(x\)”dove sono i punti di confine (aggiungendo 1, o andando a destra 1), dal momento che facciamo la matematica opposta per i “\(x\)”. Per ottenere le nuove funzioni in ogni intervallo, possiamo semplicemente sostituire “\(x-1\) ” per “\(x\) ” nell’equazione originale, moltiplicare per -2 e quindi aggiungere 3. Ad esempio,\(\displaystyle-2f\left ({x-1}\right)+3=-2 \left+3=-2\left ({x+3} \ right)+3=-2x-3\).
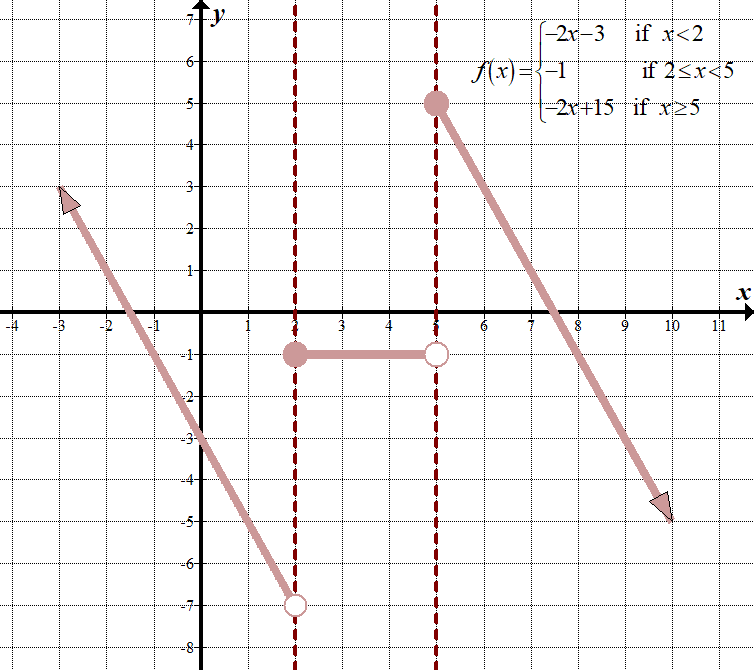
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2\left( {\left( {x-1} \right)+4} \right)+3=-2x-3,\,\,\,\,\text{ se }x-1<1\,\,\,\left( {x<2} \right)\\-2\left( 2 \a destra)+3=-1,\,\,\,\,\text{ se }\,\text{ 2 }\le x<5\\-2\left( {\left( {x-1} \right)-5} \right)+3=-2x+15,\,\,\,\,\text{ se }x\ge 5\end{array} \right.\)
Ecco i grafici” prima “e” dopo”, incluso il grafico a T:
| Piecewise Parent Function | T-chart | Transformation of Function | ||||||||||||||||||||||||||||||||||||||||
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)
|
|
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)
|
||||||||||||||||||||||||||||||||||||||||
Piecewise Function Word Problems
 Problem:
Problem:
Il tuo cane preferito groomer oneri in base al peso del vostro cane. Se il vostro cane è di 15 sterline e sotto, le spese groomer $35. Se il vostro cane è tra 15 e 40 sterline, lei fa pagare 4 40. Se il vostro cane è più di 40 sterline, lei fa pagare 4 40, più un ulteriore $2 per ogni libbra.
(a) Scrivere una funzione a tratti che descrive ciò che il vostro cane groomer oneri.
(b) Grafico della funzione.
(c) Che cosa sarebbe il groomer carica se il vostro cane carino pesa 60 chili?
Soluzione:
(a) Vediamo che i “punti di confine” sono 15 e 40, poiché questi sono i pesi in cui i prezzi cambiano. Dato che abbiamo due punti di confine, avremo tre equazioni nella nostra funzione a tratti. Dobbiamo iniziare da 0, dal momento che i cani devono pesare più di 0 chili:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{se }0<x\le 15\\\text{ }……\,\,\,\,\,\,\,\,\,\text{se }15<x\le 40\\\text{ }……\,\,\,\,\,\,\,\,\,\text{se }x>40\end{array} \right.\ )
Stiamo cercando le “risposte” (quanto costa la toelettatura) alle “domande” (quanto pesa il cane) per le tre gamme di prezzi. I primi due sono solo tasse piatte (respectively 35 e respectively 40, rispettivamente). L’ultima equazione è un po più complicata; le spese groomer 4 40 più $2 per ogni libbra oltre 40. Proviamo numeri reali: se il vostro cane pesa 60 chili, lei addebiterà $40 più times 2 volte \(20(60-40)\). Trasformeremo questo in un’equazione: \(40 + 2 (x–40)\), che semplifica a \(2x-40\) (vedi come 2 è la pendenza?).
L’intera funzione a tratti è:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }15<x\le 40\\\text{ }40+2\left( {x-40} \right)\,\,\,\,\,\,\text{se }x>40\end{array} \right.\) o \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }15<x\le 40\\\text{ }2x-40\,\,\,\,\,\,\,\text{se }x>40\end{array} \right.\)
(b) Facciamo un grafico: Si noti che questa equazione a tratti non è continua. Si noti inoltre che un dominio ragionevole per questo problema potrebbe essere \(\left ({0,200} \right]\) (dato che i cani non pesano più di 200 sterline!) e un intervallo ragionevole potrebbe essere \(\left \ cup \ left\).
Si noti che questa equazione a tratti non è continua. Si noti inoltre che un dominio ragionevole per questo problema potrebbe essere \(\left ({0,200} \right]\) (dato che i cani non pesano più di 200 sterline!) e un intervallo ragionevole potrebbe essere \(\left \ cup \ left\).
(c) Se il tuo cane pesa 60 libbre, possiamo usare il grafico o la funzione per vedere che dovresti pagare 8 80. Whoa! Che costa più di un taglio di capelli umano (almeno i miei tagli di capelli)!
Problema:
Hai intenzione di vendere le magliette She Love Math come raccolta fondi. La società di t-shirt all’ingrosso ti addebita 1 10 a camicia per le prime camicie 75. Dopo i primi 75 camicie si acquista fino a 150 camicie, l’azienda abbasserà il suo prezzo a $7,50 per camicia. Dopo aver acquistato 150 camicie, il prezzo diminuirà a 5 5 per camicia. Scrivi una funzione che modelli questa situazione.
Soluzione:
Vediamo che i “punti di confine” sono 75 e 150, poiché questi sono il numero di t-shirt acquistate dove i prezzi cambiano. Dato che abbiamo due punti di confine, avremo tre equazioni nella nostra funzione a tratti. Inizieremo con \ (x \ ge 1\), dal momento che, assumiamo almeno una camicia viene acquistata. Nota in questo problema, il numero di t-shirt acquistate (\(x\)), o il dominio, deve essere un numero intero, ma questa restrizione non dovrebbe influenzare l’esito del problema.
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text{ se }1\le x\le 75\\\text{ }……\text{ se }75<x\le 150\\\text{ }……\text{ se }x>150\end{array} \right.\)
Stiamo cercando le “risposte” (costo totale delle t-shirt) alle “domande” (quante vengono acquistate) per le tre gamme di prezzi.
Per un massimo di 75 camicie, il prezzo è di $10, quindi il prezzo totale sarebbe \(10x\). Per più di 75 camicie, ma fino a 100 camicie, il costo è di 7 7,50, ma il primo 75 t-shirt sarà ancora un costo di $10 per camicia. La seconda funzione include i 7 750 spesi per le prime camicie 75 (75 volte $10) e include anche $7.50 volte il numero di camicie oltre 75, che sarebbe \((x-75)\). Ad esempio, se hai acquistato 80 camicie, dovresti spendere \(\times 10 \ times 75= \ $750\), plus \(\$7.50 \ times 5\,\) (80 – 75) per le camicie dopo la 75a camicia.
Allo stesso modo, per oltre 150 camicie, pagheremmo comunque il prezzo di $10 fino a 75 camicie, i 7 7.50 prezzo per 76 a 150 camicie (75 più camicie), e poi 5 5 per camicia per il numero di camicie acquistati oltre 150. Pagheremo \(10(75)+7.50(75)+5(x-150)\) per\ (x\) camicie. Mettere in numeri e provare!
Il tutto a tratti funzione è:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }1\le x\le 75\\\text{ }7,5 x\text{ }+\text{ }187.5\,\,\,\,\,\text{se il 7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text {if} x > 150\end{array} \right.\) o \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }1\le x\le 75\\\text{ }7,5 x\text{ }+\text{ }187.5\,\,\,\,\,\text{se il 7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{se }x>150\end{array} \right.\ )
Problema:
Un servizio di autobus costa $50 per le prime 400 miglia, e ogni 300 miglia aggiuntive (o una frazione di esse) aggiunge $10 alla tariffa.
Utilizzare una funzione a tratti per rappresentare la tariffa dell’autobus in termini di distanza in miglia.
Soluzione:
Questo è in realtà un problema complicato, ma pensiamo prima al “punto di confine”, che è 400. È piuttosto semplice quando la corsa è inferiore a 400 miglia; il costo è di 5 50.
Per più di 400 miglia, dobbiamo sottrarre le prime 400 miglia (ma ricordiamoci di includere i primi 5 50), dividere il numero di miglia rimaste per 300 miglia (e arrotondare, se c’è un importo frazionario) e moltiplicarlo per $10.
La parte difficile è quando “arrotondiamo” per una parte delle prossime 300 miglia. Possiamo usare una funzione “ceiling” (designata da \(\left \ lceil {} \ right \ rceil\)); questa funzione fornisce il minimo intero maggiore o uguale al suo input; ad esempio, il soffitto di 3.5 e 4 è 4.
Quindi, questo è ciò che abbiamo:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{se }0\le x\le 400\\\text{ }50+10\times \left\lceil {\frac{{x-400}}{{300}}} \destra\rceil \text{ }\,\,\,\,\,\,\text{ se }x>400\end{array} \right.\)
Proviamo! Se abbiamo una corsa di 1500 miglia, il costo sarebbe \(\displaystyle 50 + 10 \ times \ left \ lceil {\frac{{1500-400}}{{300}}} \destra \ rceil \ testo {} =50 + 10 \ volte 4= \ 9 90\).
Problema:
Quale valore di \(\boldsymbol{a}\) renderebbe continua questa funzione a tratti?
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\text{ se }x<-2\\5x+\boldsymbol{a}\,\,\,\,\,\,\,\,\text{se }x\ge -2\end{array} \right.\)
Soluzione:
Affinché la funzione a tratti sia continua, nel punto limite (dove la funzione cambia), i due valori \(y\) devono essere gli stessi. Siamo in grado di collegare -2 per \(x\) in entrambe le funzioni, e assicurarsi che il \(y\)’s sono la stessa
\(\begin{align}3{{x}^{2}}+4&=5x+un\\3{{\left( {-2} \right)}^{2}}+4&=5\left( {-2} \right)+un\\12+4&=-10+un\\&=26\end{align}\)
Se \(a=26\), piecewise funzione è continua!
Impara queste regole e pratica, pratica,pratica!
Più pratica: usa il widget Mathway qui sotto per provare a scrivere una funzione a tratti. Fare clic su Invia (la freccia blu a destra del problema) e fare clic su Scrivi il valore assoluto a tratti per vedere la risposta.
Puoi anche digitare il tuo problema, oppure fare clic sui tre punti nell’angolo in alto a destra e fare clic su “Esempi” per eseguire il drill-down per argomento.
Se si fa clic su Tap per visualizzare i passaggi, o fare clic qui, è possibile registrarsi a Mathway per una prova gratuita, e quindi l’aggiornamento a un abbonamento a pagamento in qualsiasi momento (per ottenere qualsiasi tipo di problema di matematica risolto!).
Su matrici e sistemi di risoluzione con matrici – sei pronto!