- Obiettivi formativi
- Il lavoro fatto contro la gravità
- Conversione tra energia potenziale ed energia cinetica
- Utilizzare l’energia potenziale per semplificare i calcoli
- Esempio 1. La forza per smettere di cadere
- Strategia
- Soluzione
- Discussione
- Esempio 2. Trovare la velocità di un ottovolante dalla sua altezza
- Strategia
- Soluzione per la Parte 1
- Soluzione per la Parte 2
- Discussione e implicazioni
- Making Connections: Take-Home Investigation—Conversione del potenziale in energia cinetica
- Sommario della sezione
- Concettuale Domande
- Problemi& Esercizi
- Glossario
- Soluzioni selezionate ai problemi& Esercizi
Obiettivi formativi
Alla fine di questa sezione, sarai in grado di:
- Spiegare l’energia potenziale gravitazionale in termini di lavoro svolto contro la gravità.
- Mostrano che l’energia potenziale gravitazionale di un oggetto di massa m all’altezza h sulla Terra è data da PEg = mgh.
- Mostra come la conoscenza dell’energia potenziale in funzione della posizione può essere utilizzata per semplificare i calcoli e spiegare i fenomeni fisici.
Il lavoro fatto contro la gravità
Salire le scale e sollevare oggetti è un lavoro sia in senso scientifico che quotidiano—è un lavoro fatto contro la forza gravitazionale. Quando c’è lavoro, c’è una trasformazione di energia. Il lavoro svolto contro la forza gravitazionale va in una forma importante di energia immagazzinata che esploreremo in questa sezione.

Figura 1. (a) Il lavoro svolto per sollevare il peso è immagazzinato nel sistema massa-Terra come energia potenziale gravitazionale. (b) Mentre il peso si sposta verso il basso, questa energia potenziale gravitazionale viene trasferita all’orologio a cucù.
Calcoliamo il lavoro svolto nel sollevare un oggetto di massa m attraverso un’altezza h, come nella Figura 1. Se l’oggetto viene sollevato verso l’alto a velocità costante, la forza necessaria per sollevarlo è uguale al suo peso mg. Il lavoro fatto sulla massa è quindi W = Fd = mgh. Definiamo che questa sia l’energia potenziale gravitazionale (PEg) immessa (o acquisita da) il sistema oggetto-Terra. Questa energia è associata allo stato di separazione tra due oggetti che si attraggono l’un l’altro dalla forza gravitazionale. Per comodità, ci riferiamo a questo come il PIOLO guadagnato dall’oggetto, riconoscendo che questa è energia immagazzinata nel campo gravitazionale della Terra. Perché usiamo la parola “sistema”? L’energia potenziale è una proprietà di un sistema piuttosto che di un singolo oggetto—a causa della sua posizione fisica. Il potenziale gravitazionale di un oggetto è dovuto alla sua posizione rispetto all’ambiente circostante all’interno del sistema Terra-oggetto. La forza applicata all’oggetto è una forza esterna, dall’esterno del sistema. Quando fa un lavoro positivo aumenta l’energia potenziale gravitazionale del sistema. Poiché l’energia potenziale gravitazionale dipende dalla posizione relativa, abbiamo bisogno di un livello di riferimento al quale impostare l’energia potenziale uguale a 0. Di solito scegliamo questo punto come superficie terrestre, ma questo punto è arbitrario; ciò che è importante è la differenza nell’energia potenziale gravitazionale, perché questa differenza è ciò che riguarda il lavoro svolto. La differenza di energia potenziale gravitazionale di un oggetto (nel sistema Terra-oggetto) tra due gradini di una scala sarà la stessa per i primi due gradini come per gli ultimi due gradini.
Conversione tra energia potenziale ed energia cinetica
L’energia potenziale gravitazionale può essere convertita in altre forme di energia, come l’energia cinetica. Se rilasciamo la massa, la forza gravitazionale farà una quantità di lavoro pari a mgh su di essa, aumentando così la sua energia cinetica di quella stessa quantità (dal teorema dell’energia del lavoro). Troveremo più utile considerare solo la conversione di PEg in KE senza considerare esplicitamente la fase intermedia del lavoro. (Vedi esempio 2.) Questa scorciatoia rende più facile risolvere i problemi usando l’energia (se possibile) piuttosto che usare esplicitamente le forze.
Più precisamente, definiamo il cambiamento nell’energia potenziale gravitazionale ΔPEg come ΔPEg = mgh, dove, per semplicità, denotiamo il cambiamento di altezza di h piuttosto che il solito Δh. Si noti che h è positivo quando l’altezza finale è maggiore dell’altezza iniziale e viceversa. Ad esempio, se viene sollevata una massa di 0,500 kg appesa a un orologio a cucù 1.00 m, quindi il suo cambiamento in energia potenziale gravitazionale è
\begin{array}{lll}n&&(0.500\text{ kg})(9.80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\text{/s}^2=4.90\text{ J}\end{array}\\
si noti che l’unità di misura dell’energia potenziale gravitazionale rivelarsi joule, lo stesso per il lavoro e altre forme di energia. Mentre l’orologio corre, la massa si abbassa. Possiamo pensare che la massa rinunci gradualmente al suo 4.90 J di energia potenziale gravitazionale, senza considerare direttamente la forza di gravità che fa il lavoro.
Utilizzare l’energia potenziale per semplificare i calcoli

Figura 2. La variazione dell’energia potenziale gravitazionale (ΔPEg) tra i punti A e B è indipendente dal percorso.
L’equazione ΔPEg = mgh si applica per qualsiasi percorso che ha una variazione di altezza di h, non solo quando la massa viene sollevata verso l’alto. (Vedi Figura 2.) È molto più facile calcolare mgh (una semplice moltiplicazione) che calcolare il lavoro svolto lungo un percorso complicato. L’idea di energia potenziale gravitazionale ha il doppio vantaggio che è molto ampiamente applicabile e rende i calcoli più facili.
D’ora in poi, considereremo che qualsiasi cambiamento nella posizione verticale h di una massa m è accompagnato da un cambiamento nell’energia potenziale gravitazionale mgh, e eviteremo l’equivalente ma più difficile compito di calcolare il lavoro svolto da o contro la forza gravitazionale.
ΔPEg = mgh per qualsiasi percorso tra i due punti. La gravità è una di una piccola classe di forze in cui il lavoro svolto da o contro la forza dipende solo dai punti di partenza e di fine, non dal percorso tra di loro.
Esempio 1. La forza per smettere di cadere
A 60.la persona da 0 kg salta sul pavimento da un’altezza di 3,00 m. Se atterra in modo rigido (con le articolazioni del ginocchio che si comprimono di 0,500 cm), calcola la forza sulle articolazioni del ginocchio.
Strategia
L’energia di questa persona viene portata a zero in questa situazione dal lavoro svolto su di lui dal pavimento mentre si ferma. Il piolo iniziale si trasforma in KE mentre cade. Il lavoro svolto dal pavimento riduce questa energia cinetica a zero.
Soluzione
Il lavoro fatto sulla persona dal pavimento mentre si ferma è dato da W = Fd cos θ = −Fd, con un segno meno perché lo spostamento durante l’arresto e la forza dal pavimento sono in direzioni opposte (cos θ = cos 180º = -1). Il pavimento rimuove l’energia dal sistema, quindi funziona in modo negativo.
L’energia cinetica che la persona ha al raggiungimento del pavimento è la quantità di energia potenziale persa cadendo attraverso l’altezza h: KE = −ΔPEg = −mgh.
La distanza d che le ginocchia della persona si piegano è molto più piccola dell’altezza h della caduta, quindi il cambiamento aggiuntivo nell’energia potenziale gravitazionale durante la curva del ginocchio viene ignorato.
Il lavoro W fatto dal pavimento sulla persona ferma la persona e porta l’energia cinetica della persona a zero: W = −KE = mgh.
Combinando questa equazione con l’espressione per W si ottiene-Fd = mgh.
Ricordando che h è negativo perché la persona è caduta, la forza sulle articolazioni del ginocchio è data da
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\right)\left(9.80\text{ m/s}^2\right)\left(-3.00\text{ m}\right)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ N}\\
Discussione
una grande forza (500 volte di più rispetto al peso della persona) nel breve impatto tempo è sufficiente per rompere le ossa. Un modo molto migliore per attutire lo shock è piegando le gambe o rotolando a terra, aumentando il tempo su cui agisce la forza. Un movimento di flessione di 0,5 m in questo modo produce una forza 100 volte inferiore rispetto all’esempio. Il salto di un canguro mostra questo metodo in azione. Il canguro è l’unico grande animale ad usare il salto per la locomozione, ma lo shock nel salto è ammortizzato dalla flessione delle zampe posteriori in ogni salto. (Vedi Figura 3.)

Figura 3. Il lavoro fatto dal terreno sul canguro riduce la sua energia cinetica a zero mentre atterra. Tuttavia, applicando la forza del terreno sulle zampe posteriori su una distanza più lunga, l’impatto sulle ossa è ridotto. (credito: Chris Samuel, Flickr)
Esempio 2. Trovare la velocità di un ottovolante dalla sua altezza
- Qual è la velocità finale dell’ottovolante mostrata in Figura 4 se parte dal riposo in cima alla collina di 20,0 m e il lavoro svolto dalle forze di attrito è trascurabile?
- Qual è la sua velocità finale (sempre ipotizzando un attrito trascurabile) se la sua velocità iniziale è di 5,00 m / s?
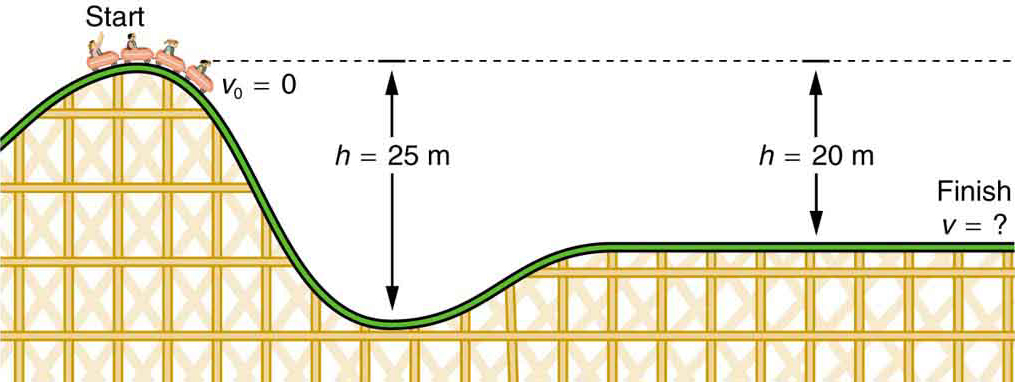
Figura 4. La velocità di un ottovolante aumenta come gravità tira in discesa ed è più grande nel suo punto più basso. Visto in termini di energia, l’energia potenziale gravitazionale del sistema roller-coaster-Earth viene convertita in energia cinetica. Se il lavoro svolto dall’attrito è trascurabile, tutto ΔPEg viene convertito in KE.
Strategia
Le montagne russe perdono energia potenziale mentre scendono. Trascuriamo l’attrito, in modo che la forza rimanente esercitata dalla traccia sia la forza normale, che è perpendicolare alla direzione del movimento e non funziona. Il lavoro netto sulle montagne russe viene quindi eseguito solo per gravità. La perdita di energia potenziale gravitazionale dal movimento verso il basso attraverso una distanza h è uguale al guadagno in energia cinetica. Questo può essere scritto in forma di equazione come-ΔPEg = ΔKE. Usando le equazioni per PEg e KE, possiamo risolvere per la velocità finale v, che è la quantità desiderata.
Soluzione per la Parte 1
Qui l’energia cinetica iniziale è zero, in modo che \Delta\text{KE}=\frac{1}{2}mv^2\\. L’equazione per il cambiamento di energia potenziale afferma che ΔPEg = mgh. Poiché h è negativo in questo caso, riscriveremo questo come ΔPEg = −mg|h| per mostrare chiaramente il segno meno. Quindi, – ΔPEg = ΔKE diventa mg|h / = \ frac{1} {2} {mv}^2\\.
Risolvendo per v, troviamo che la massa annulla e che v = \ sqrt{2g / h/}\\.
Sostituendo i valori noti,
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
Soluzione per la Parte 2
di Nuovo −ΔPEg = ΔKE. In questo caso c’è energia cinetica iniziale, quindi
\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
Quindi, mg|h / =\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
Riorganizzare dà \frac{1}{2}mv^2=mg|h / +\frac{1}{2}mv+0^2\\.
Ciò significa che l’energia cinetica finale è la somma dell’energia cinetica iniziale e dell’energia potenziale gravitazionale. Massa di nuovo annulla, e v= \ sqrt{2g / h/ + v_0^2}\\.
Questa equazione è molto simile all’equazione cinematica v=\sqrt{v_0^2+2ad}\\, ma è più generale—l’equazione cinematica è valida solo per l’accelerazione costante, mentre la nostra equazione sopra è valida per qualsiasi percorso indipendentemente dal fatto che l’oggetto si muova con un’accelerazione costante. Ora, sostituendo i valori noti dà
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left(5.00\text{ m/s}\right)^2}\\\text{ }&&20.4\text{ m/s}\end{array}\ \
Discussione e implicazioni
Innanzitutto, si noti che la massa annulla. Questo è abbastanza coerente con le osservazioni fatte in Caduta di oggetti che tutti gli oggetti cadono alla stessa velocità se l’attrito è trascurabile. In secondo luogo, viene considerata solo la velocità delle montagne russe; non ci sono informazioni sulla sua direzione in nessun punto. Questo rivela un’altra verità generale. Quando l’attrito è trascurabile, la velocità di un corpo che cade dipende solo dalla sua velocità e altezza iniziali, e non dalla sua massa o dal percorso intrapreso. Ad esempio, le montagne russe avranno la stessa velocità finale se cade 20,0 m verso il basso o prende un percorso più complicato come quello nella figura. Terzo, e forse inaspettatamente, la velocità finale nella parte 2 è maggiore della parte 1, ma di gran lunga inferiore a 5,00 m/s. Infine, si noti che la velocità può essere trovata a qualsiasi altezza lungo la strada semplicemente usando il valore appropriato di h nel punto di interesse.
Abbiamo visto che il lavoro svolto da o contro la forza gravitazionale dipende solo dai punti di partenza e di fine, e non dal percorso tra, permettendoci di definire il concetto semplificativo di energia potenziale gravitazionale. Possiamo fare la stessa cosa per alcune altre forze, e vedremo che questo porta a una definizione formale della legge di conservazione dell’energia.
Making Connections: Take-Home Investigation—Conversione del potenziale in energia cinetica
In questo esperimento si può studiare la conversione dell’energia potenziale gravitazionale in energia cinetica. Su una superficie liscia e piana, utilizzare un righello del tipo che ha una scanalatura che corre lungo la sua lunghezza e un libro per fare una pendenza (vedi Figura 5). Posizionare un marmo nella posizione di 10 cm sul righello e lasciarlo rotolare giù per il righello. Quando colpisce la superficie piana, misurare il tempo necessario per rotolare un metro. Ora posizionare il marmo nelle posizioni di 20 cm e 30 cm e misurare nuovamente i tempi necessari per rotolare 1 m sulla superficie piana. Trova la velocità del marmo sulla superficie piana per tutte e tre le posizioni. Tracciare la velocità al quadrato rispetto alla distanza percorsa dal marmo. Qual è la forma di ogni trama? Se la forma è una linea retta, la trama mostra che l’energia cinetica del marmo in basso è proporzionale alla sua energia potenziale nel punto di rilascio.

Figura 5. Un marmo rotola giù un righello e viene misurata la sua velocità sulla superficie piana.
Sommario della sezione
- Il lavoro fatto contro la gravità nel sollevamento di un oggetto diventa energia potenziale del sistema oggetto-Terra.
- La variazione dell’energia potenziale gravitazionale, ΔPEg, è ΔPEg = mgh, con h che è l’aumento di altezza e g l’accelerazione dovuta alla gravità.
- L’energia potenziale gravitazionale di un oggetto vicino alla superficie terrestre è dovuta alla sua posizione nel sistema massa-Terra. Solo le differenze nell’energia potenziale gravitazionale, ΔPEg, hanno significato fisico.
- Come un oggetto scende in assenza di attrito, la sua energia potenziale gravitazionale trasforma in energia cinetica corrispondente all’aumento di velocità, in modo che ΔKE = −ΔPEg
Concettuale Domande
- Nell’Esempio 2, abbiamo calcolato la velocità finale di un roller coaster che scende a 20 m di altezza e aveva una velocità iniziale di 5 m/s in discesa. Supponiamo che le montagne russe avessero avuto una velocità iniziale di 5 m/s in salita, e costeggiasse in salita, si fermasse e poi tornasse indietro fino a un punto finale 20 m sotto la partenza. Troveremmo in quel caso che aveva la stessa velocità finale. Spiegare in termini di conservazione dell’energia.
- Il lavoro che fai su un libro quando lo sollevi su uno scaffale dipende dal percorso intrapreso? Sul tempo impiegato? Sull’altezza dello scaffale? Sulla messa del libro?
Problemi& Esercizi
- Un impianto idroelettrico (vedi Figura 6) converte l’energia potenziale gravitazionale dell’acqua dietro una diga in energia elettrica. (a) Qual è l’energia potenziale gravitazionale relativa ai generatori di un lago di volume 50.0 km3 (massa = 5,00 × 1013 kg), dato che il lago ha un’altezza media di 40,0 m sopra i generatori? (b) Confrontalo con l’energia immagazzinata in una bomba a fusione da 9 megatoni.

Figura 6. Impianto idroelettrico (credit: Denis Belevich, Wikimedia Commons)
- (a) Quanta energia potenziale gravitazionale (relativa al terreno su cui è costruita) è immagazzinata nella Grande Piramide di Cheope, dato che la sua massa è di circa 7 × 109 kg e il suo centro di massa è 36.5 m sopra il terreno circostante? (b) In che modo questa energia si confronta con l’assunzione giornaliera di cibo di una persona?
- Supponiamo che un kookaburra di 350 g (un grande uccello martin pescatore) raccolga un serpente di 75 g e lo sollevi a 2,5 m da terra fino a un ramo. (a) Quanto lavoro fece l’uccello sul serpente? (b) Quanto lavoro fece per elevare il proprio centro di massa alla filiale?
- Nell’esempio 2, abbiamo scoperto che la velocità di un ottovolante che aveva disceso 20.0 m era solo leggermente maggiore quando aveva una velocità iniziale di 5.00 m/s rispetto a quando partiva dal riposo. Ciò implica che ΔPE >> KEi. Confermare questa affermazione prendendo il rapporto tra ΔPE e KEi. (Si noti che la massa annulla.)
- Un’auto giocattolo da 100 g è azionata da una molla compressa che la avvia in movimento. L’auto segue la pista curva in Figura 7. Mostra che la velocità finale della macchinetta è 0,687 m/s se la sua velocità iniziale è 2,00 m / s e costeggia il pendio senza attrito, guadagnando 0,180 m di altitudine.

Figura 7. Un’auto giocattolo si muove su una pista inclinata. (credit: Leszek Leszczynski, Flickr)
- In una gara di sci alpino, sorprendentemente, poco vantaggio è guadagnato da ottenere una partenza in corsa. (Questo perché l’energia cinetica iniziale è piccola rispetto al guadagno in energia potenziale gravitazionale anche su piccole colline.) Per dimostrarlo, trova la velocità finale e il tempo impiegato per uno sciatore che percorre 70,0 m lungo una pendenza di 30º trascurando l’attrito: (a) Partendo dal riposo. (b) A partire da una velocità iniziale di 2,50 m / s. (c) La risposta ti sorprende? Discutere perché è ancora vantaggioso per ottenere un inizio di corsa in eventi molto competitivi.
Glossario
energia potenziale gravitazionale: l’energia che un oggetto ha a causa della sua posizione in un campo gravitazionale
Soluzioni selezionate ai problemi& Esercizi
1. (a) 1,96 × 1016 J; (b) Il rapporto tra l’energia potenziale gravitazionale nel lago e l’energia immagazzinata nella bomba è 0,52. Cioè, l’energia immagazzinata nel lago è circa la metà di quella in una bomba a fusione da 9 megatoni.
3. a)1,8 J; b) 8,6 J
5. {v}_{f}=\sqrt{2gh+{v_0}^2}=\sqrt{2\left(9.80\text{ m/s}^2\right)\left(-0.180\text{ m}\right)+\left(2.00\text{ m/s}\right)^2}=0.687\text{ m/s}\\