Boyle’s Law
Robert Boyle (1627 – 1691), un chimico inglese, è ampiamente considerato uno dei fondatori della moderna scienza sperimentale della chimica. Ha scoperto che raddoppiando la pressione di un campione chiuso di gas mantenendo costante la sua temperatura ha causato la riduzione del volume del gas della metà. La legge di Boyle afferma che il volume di una data massa di gas varia inversamente con la pressione quando la temperatura è mantenuta costante. Una relazione inversa è descritta in questo modo. Quando una variabile aumenta di valore, l’altra variabile diminuisce.
Fisicamente, cosa sta succedendo? Le molecole di gas sono in movimento e sono una certa distanza l’una dall’altra. Un aumento della pressione spinge le molecole più vicine, riducendo il volume. Se la pressione è diminuita, i gas sono liberi di muoversi in un volume maggiore.

Matematicamente, la legge di Boyle può essere espressa dall’equazione:
\
Il \(k\) è una costante per un dato campione di gas e dipende solo dalla massa del gas e dalla temperatura. La tabella seguente mostra i dati di pressione e volume per una quantità impostata di gas a temperatura costante. La terza colonna rappresenta il valore della costante \(\left( k \right)\) per questi dati ed è sempre uguale alla pressione moltiplicata per il volume. Quando una delle variabili cambia, l’altra cambia in modo tale che il prodotto di \(P \volte V\) rimanga sempre lo stesso. In questo caso particolare, tale costante è \(500\: \ text{atm} \ cdot \ text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
Un grafico dei dati nella tabella illustra ulteriormente relazione inversa natura della legge di Boyle (vedi figura sotto). Il volume viene tracciato sull’asse \(x\), con la pressione corrispondente sull’asse\(y\).
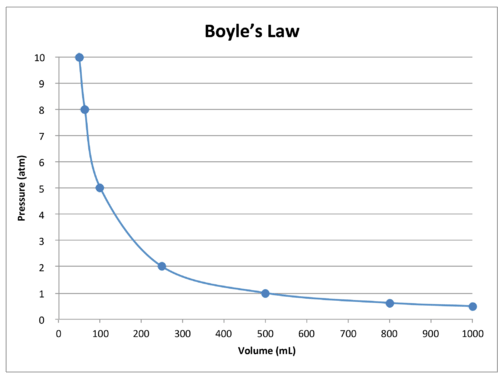
La legge di Boyle può essere usata per confrontare le condizioni mutevoli di un gas. Usiamo \(P_1\) e \(V_1\) per rappresentare la pressione iniziale e il volume iniziale di un gas. Dopo aver apportato una modifica, \(P_2\) e \(V_2\) rappresentano la pressione e il volume finali. La relazione matematica della Legge di Boyle diventa:
\
Questa equazione può essere utilizzata per calcolare una qualsiasi delle quattro quantità se le altre tre sono note.
Esempio \(\PageIndex{1}\)
Un campione di gas ossigeno ha un volume di \(425 \: \ text {mL}\) quando la pressione è uguale a \(387 \: \ text{kPa}\). Il gas può espandersi in un contenitore \(1.75 \: \text{L}\). Calcola la nuova pressione del gas.
Soluzione
Passo 1: Elencare le quantità note e pianificare il problema.
Note
- \(1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1.75 \: \text{L} = 1750 \: \text{mL}\)
Sconosciuto
- \(P_2 = ? \: \text{kPa}\)
Usa la Legge di Boyle per risolvere la pressione sconosciuta \(\left( P_2 \ right)\). È importante che i due volumi (\(V_1\) e \(V_2\)) siano espressi nelle stesse unità, quindi \(V_2\) è stato convertito in \(\text{mL}\).
Passo 2: Risolvere.
In primo luogo, riorganizzare l’equazione algebricamente per risolvere per \(P_2\).
\
Ora sostituire le quantità note nell’equazione e risolvere.
\
Passaggio 3: Pensa al tuo risultato.
Il volume è aumentato a poco più di 4 volte il suo valore originale e quindi la pressione è diminuita di circa un quarto. La pressione è in \(\text {kPa}\) e il valore ha tre cifre significative. Si noti che è possibile utilizzare qualsiasi unità di pressione o volume purché siano coerenti per tutto il problema.