Purplemath
a matematikában az “identitás” egy mindig igaz egyenlet. Ezek lehetnek “triviálisan” igazak, például “x = x” vagy hasznosan igazak, mint például a pitagorai tétel “a2 + b2 = c2” a jobb háromszögekhez. Rengeteg trigonometrikus identitás létezik, de a következők azok, amelyeket a legvalószínűbb látni és használni.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Alapvető Pitagorasz Identitások
Affiliate
Figyeljük meg, hogy a “co-(valamit)”trig arány mindig a kölcsönös néhány “nem-co” arány. Használhatja ezt a tényt, hogy segítsen tisztán tartani, hogy a cosecant a szinuszhoz, a secant pedig a koszinuszhoz tartozik.
a következőket (különösen az alábbi három közül az elsőt) “pitagorai” identitásoknak nevezik.
sin2 (t) + cos2 (t) = 1
tan2 (t) + 1 = sec2 (t)
1 + cot2 ( t) = csc2 (t)
hirdetés
1. A Pitagorasz-Thereom összefüggést egyértelműen láthatja, ha figyelembe vesszük az egységkört, ahol a szög t, az “ellenkező” oldal sin ( t) = y, a “szomszédos” oldal cos(t) = x, a hipotenusz pedig 1.
még további személyazonossággal kapcsolatban, a funkcionális állapot, a trig arányok:
sin(–t) = –sin(t)
cos(–t) = cos(t)
tan(–t) = –tan(t)
Értesítés, különösen, hogy szinusz, valamint érintő különleges funkciók hogy szimmetrikus, honnan ered, míg a koszinusz egy olyan funkció is, hogy szimmetrikus az y-tengely. Az a tény, hogy az argumentum “mínusz” jelét kívülről (szinuszra és érintőre) vagy teljesen kiküszöbölheti (koszinuszra), hasznos lehet bonyolult kifejezésekkel való munka során.
Szög-Összeget, valamint -a Különbség Identitások
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
mellesleg, a fenti azonosságok, a szögek jelöli görög betűk. Az a-típusú betű, “α”, az úgynevezett “alfa”, amely ejtik “AL-fuh”. A b-típusú betű, “β”, az úgynevezett” béta”, amely ejtik”BAY-tuh”.
Tartalom Továbbra is Alul
Kettős-Szög Identitások
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Fele-Szög Identitások
A fenti azonosságok lehet újra kijelentette, hogy a művészet minden oldalán pedig megduplázódott az összes szög intézkedések. Az eredmények a következők:
Affiliate

Sum Identities
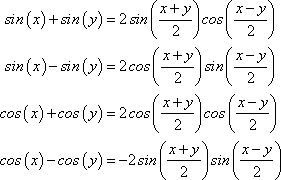
Product Identities
Affiliate
fogja használni ezeket a kilétüket, vagy majdnem olyan, bizonyítania kell, más trigonometrikus azonosságok, illetve megoldására trigonometrikus egyenletek. Azonban, ha mész, hogy tanulmányozza kalkulus, különös figyelmet kell fordítani a felújított szinusz és koszinusz félszög identitások, mert akkor használja őket sokat integrál kalkulus.
URL: https://www.purplemath.com/modules/idents.htm