néhány érdekes dolgot szögek és körök.
beírt szög
először, definíció:
beírt szög: a kör kerületén ülő pontokból készült szög.
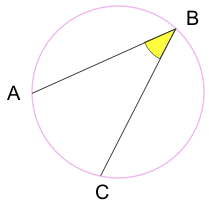
A és C A “végpontok”
B a”csúcspont”
játssz vele itt:
amikor a “B” pontot mozgatod, mi történik a szöggel?
Írva Szög Tételek
Egy írva szög° fele a központi szög 2a°
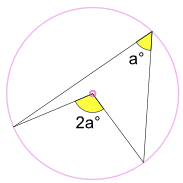
(az a Szög, a Középső Tétel)
S (tartja a végpontok fix) …
… az a° szög mindig ugyanaz,
nem számít, hol van ugyanazon az íven a végpontok között:
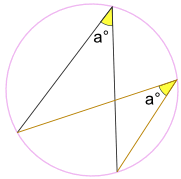
A ° szög ugyanaz.
(az úgynevezett szögek Subtended által azonos ív tétel)
példa: Mi a méret szög POQ? (O a kör középpontja)
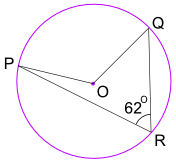
szög POQ = 2 × szög PRQ = 2 × 62° = 124°
példa: Mi a CBX szög mérete?
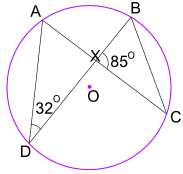
szög ADB = 32° is egyenlő szög ACB.
és szög ACB is egyenlő szög XCB.
tehát a BXC háromszögben ismerjük a BXC = 85° szöget, az XCB = 32°
most egy háromszög szögeit használjuk hozzá 180° – hoz :
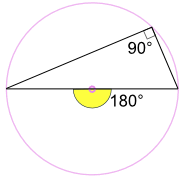
Szög Félkörben (Thales’ Tétel)
Egy szög írt át egy kör átmérője mindig jobb szög:
(A végén a pontok mindkét végén egy-egy kör átmérője,
az apex pont bárhol lehet a kerülete.)
|
miért? Mert: A beírt szög 90° fele a központi szög 180° (A “Szög, a Középső Tétel” felett) |
 |
Egy Jó Ok, Hogy Miért Működik
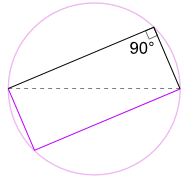
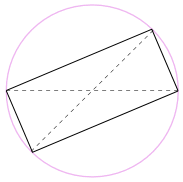
Mi is lehet forgatni a forma körül 180° – kal, hogy egy téglalapot!
Ez egy téglalap, mert minden oldal párhuzamos, mindkét átló egyenlő.
tehát belső szögei derékszögűek (90°).
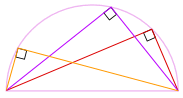
így megyünk! Nem számít, hol van ez a szög
a kerületen, mindig 90°
példa: Mi a BAC szög mérete?
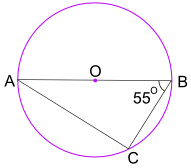
a szög a félkör tétel azt mondja, hogy szög ACB = 90°
most használja szögek egy háromszög hozzá 180° megtalálni szög BAC:
Találni egy Kör közepén
használhatjuk ezt az ötletet, hogy megtalálja a kör közepén:
- rajzolni, derékszögben bárhol a kör kerülete, akkor döntetlen az átmérő, ahol a két lába megütötte a kör
- megint, de a különböző átmérőjű
Amennyiben az átmérők kereszt, a központ!
Ciklikus Négyszög
|
A “Ciklikus” Négyszög minden vertex egy kör kerülete: |
 |
|
A Ciklikus Négyszög másik szögből hozzá, hogy 180°:
|
 |
Példa: Mi a méret Szög WXY?
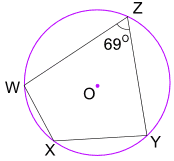
Opposite angles of a cyclic quadrilateral add to 180°

