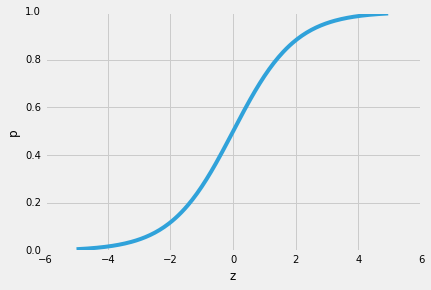
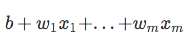tehát a logisztikus regresszió egyik szép tulajdonsága, hogy a sigmoid függvény a predikció feltételes valószínűségeit, az osztály valószínűségeit adja ki. Hogy működik?Kezdjük az úgynevezett” esélyaránnyal ” p / (1-p), amely leírja egy bizonyos, pozitív esemény bekövetkezésének valószínűségét és annak valószínűségét, hogy nem fordul elő – ahol a pozitív az “esemény, amelyet meg akarunk jósolni”, azaz p(y=1 | x).
(vegye figyelembe, hogy a logisztikus regresszió egy speciális sigmoid függvény, a logisztikus sigmoid; más sigmoid funkciók léteznek, például a hiperbolikus érintő).
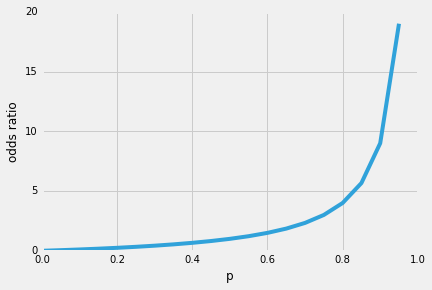
tehát minél valószínűbb, hogy a pozitív esemény bekövetkezik, annál nagyobb az esélyek aránya.Most, ha a természetes bejelentkezés ezt a valószínűsége ennek az arány, a log odds, vagy logit funkció, a következő
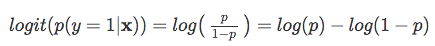
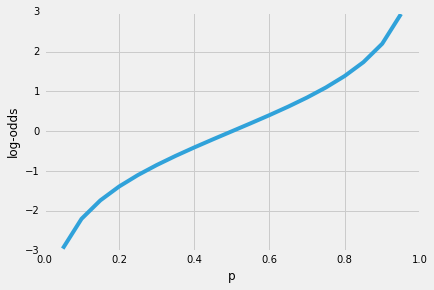
a Következő használjuk ezt a naplót transzformációs modell közötti kapcsolat, a magyarázó változók pedig a cél változó: 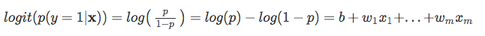
| Most, tartsa észben, hogy nem próbáljuk megjósolni a jobb oldali része a fenti egyenlet, mivel *p(y=1 | x)* mi tényleg érdekel. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
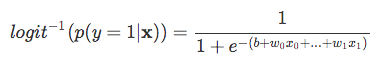
| which returns the class probabilities *p(y=1 | x)* from the inputs |