tanulási célok

e szakasz végére képes lesz:

• megmagyarázni a gravitációs potenciális energiát a gravitáció ellen végzett munka szempontjából.
• azt mutatják, hogy a gravitációs potenciális energia egy tárgy tömege m magasságban h a Földön adják PEg = mgh.
• mutassa be, hogy a potenciális energia pozíciófüggvényként való ismerete hogyan használható a számítások egyszerűsítésére és a fizikai jelenségek magyarázatára.

1. ábra. a) A tömeg felemelésére végzett munkát a tömeg-Föld rendszerben gravitációs potenciális energiaként tárolják. b) ahogy a súly lefelé mozog, ez a gravitációs potenciális energia átkerül a kakukk órájába.

2.ábra. A gravitációs potenciál energiájának (ΔPEg) változása az A és B pontok között független az ösvénytől.

1. példa. Az erő, hogy ne essen

a 60.0 kg-os személy ugrik a padlóra 3,00 m magasságból. ha mereven landol (térdízületei 0,500 cm-rel összenyomódnak), számítsa ki a térdízületek erejét.

stratégia

Ez a személy energiáját ebben a helyzetben nullára hozza a padlón végzett munka, amikor megáll. A kezdeti csap átalakul KE ahogy esik. A padló által végzett munka nullára csökkenti ezt a kinetikus energiát.

a padlón végzett munkát w = Fd cos θ = −Fd adja meg, mínusz jellel, mert a megállás közben történő elmozdulás és a padlóról érkező erő ellentétes irányban van (cos θ = cos 180º = -1). A padló eltávolítja az energiát a rendszerből, így negatív munkát végez.

az a kinetikus energia, amelyet a személy a padló elérésekor birtokol, az a potenciális energia mennyisége, amelyet a magasságon való átesés elveszít h: KE = – ΔPEg = – mgh.

A D távolság, amelyet az ember térdhajlása sokkal kisebb, mint az esés h magassága, így a gravitációs potenciál energiájának további változása a térdhajlás során figyelmen kívül marad.

a munka w végzett a padlón a személy megállítja a személy hozza a személy kinetikus energia nulla: W = – KE = mgh.

Az egyenlet kombinálása A W gives −Fd = mgh kifejezéssel.

emlékeztetve arra, hogy H negatív, mert a személy leesett, a térdízületek erejét

\ displaystyle{F} = – \ FRAC{mgh}{d} = – \frac {\left(60.0 \ text{ kg} \ right) \ bal (9.80 \ text{ m / s}^2 \ right) \ bal (-3.00 \ text{ m} \ right)} {5.00\times10^{-3}\text{ m}=3.53\times10^5 \ text{ N} \

Vita

egy ilyen nagy erő (500-szor nagyobb, mint a személy súlya) a rövid ütési idő alatt elegendő ahhoz, hogy csonttörést. A sokk enyhítésének sokkal jobb módja a lábak hajlítása vagy a földön történő gördülés, növelve az erő hatását. A 0,5 m-es hajlítási mozgás így 100-szor kisebb erőt eredményez, mint a példában. A kenguru ugrása ezt a módszert mutatja. A kenguru az egyetlen nagy állat, amely ugrást használ a mozgáshoz, de az ugrálás sokkját tompítja a hátsó lábak hajlítása minden ugrásban. (Lásd A 3. Ábrát.)

3. ábra. A föld által a kengurun végzett munka csökkenti kinetikus energiáját nullára, amikor földet ér. Azonban, ha a talaj erejét a hátsó lábakon hosszabb távolságra alkalmazzák, a csontokra gyakorolt hatás csökken. (credit: Chris Samuel, Flickr)

2.példa. A hullámvasút sebességének meghatározása a magasságától

1. mi a 4. ábrán látható hullámvasút végső sebessége, ha a 20,0 m-es hegy tetején nyugalomtól indul, és a súrlódási erők által végzett munka elhanyagolható?
2. mi a végső sebessége (ismét elhanyagolható súrlódást feltételezve), ha kezdeti sebessége 5,00 m/s?

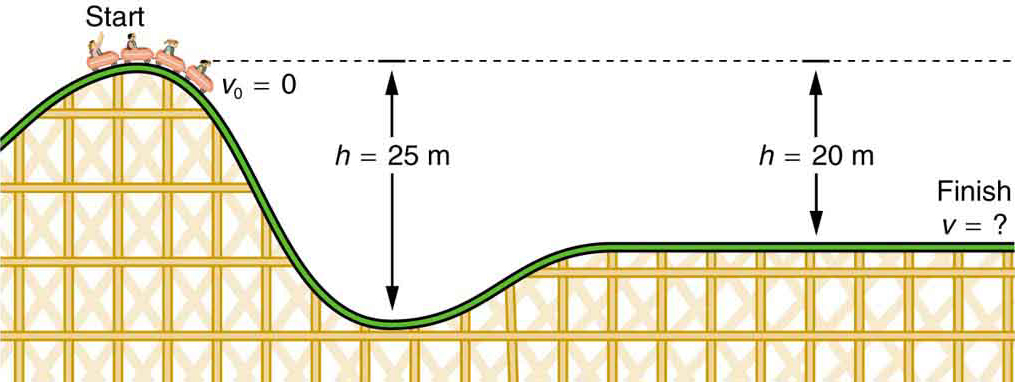
4.ábra. A hullámvasút sebessége növekszik, ahogy a gravitáció lefelé húzza, és a legalacsonyabb pontján a legnagyobb. Az energia szempontjából nézve a hullámvasút-Föld rendszer gravitációs potenciális energiája kinetikus energiává alakul. Ha a súrlódás által végzett munka elhanyagolható, akkor az összes ΔPEg ke-re alakul.

stratégia

a hullámvasút elveszíti a potenciális energiát, ahogy lefelé halad. Elhanyagoljuk a súrlódást, így a pálya által kifejtett maradék erő a normál erő, amely merőleges a mozgás irányára, és nem működik. A hullámvasút nettó munkáját ezután egyedül a gravitáció végzi. A gravitációs potenciál energiájának elvesztése a H távolságon keresztül lefelé haladva megegyezik a kinetikus energia nyereségével. Ez lehet írni egyenlet formájában-ΔPEg = ΔKE. A PEg és KE egyenleteit használva megoldhatjuk a v végsebességet, ami a kívánt mennyiség.

megoldás az 1. részhez

itt a kezdeti kinetikus energia nulla, tehát \ Delta \ text{KE} = \ frac{1}{2}mV^2\\. A potenciális energia változásának egyenlete kimondja, hogy ΔPEg = mgh. Mivel ebben az esetben a H negatív, ezt ΔPEg = −mg|h / – ként írjuk át, hogy egyértelműen megmutassuk a mínusz jelet. Így-ΔPEg = ΔKE mg|h / = \ frac{1}{2}{mV}^2\.

megoldása v, azt találjuk, hogy a tömeg törlődik, és hogy v = \ sqrt{2G|h|}\\.

ismert értékek helyettesítése,

\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\text{ }&&19.8\text{ m/s}\End{array}\\

megoldás a 2.rész

ismét −δpeg = δke. Ebben az esetben van kezdeti kinetikus energia, tehát

\Delta\text{KE}=\frac{1}{2}mV^2-\frac{1}{2}mv_0^2\\.

így mg|h|=\frac{1}{2}mV^2-\frac{1}{2}mv_0^2\\.

átrendezése ad \ frac{1}{2}mV^2=mg|h|+\frac{1}{2}mv+0^2\.

Ez azt jelenti, hogy a végső kinetikus energia a kezdeti kinetikus energia és a gravitációs potenciálenergia összege. A tömeg ismét törlődik, v = \ sqrt{2G|h|+v_0^2}\\.

Ez az egyenlet nagyon hasonlít a v=\sqrt{v_0^2+2AD} \ \ kinematikai egyenlethez, de általánosabb—a kinematikai egyenlet csak állandó gyorsulásra érvényes, míg a fenti egyenletünk minden útvonalra érvényes, függetlenül attól, hogy az objektum állandó gyorsulással mozog-e. Most az ismert értékek helyettesítése

\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\jobb)+\bal(5.00\text{ m/s}\jobb)^2}\\\text{ }&&20.4 \ text{ m / s} \ end{array} \ \

Discussion and Implications

First, note that mass cancels. Ez meglehetősen összhangban van a csökkenő tárgyakban tett megfigyelésekkel, amelyek szerint minden tárgy ugyanolyan sebességgel esik, ha a súrlódás elhanyagolható. Másodszor, csak a hullámvasút sebességét veszik figyelembe; semmilyen ponton nincs információ az irányáról. Ez egy másik általános igazságot tár fel. Ha a súrlódás elhanyagolható, a hulló test sebessége csak a kezdeti sebességétől és magasságától függ, nem pedig a tömegétől vagy a megtett úttól. Például a hullámvasútnak ugyanolyan végső sebessége lesz, függetlenül attól, hogy egyenesen 20,0 m-re esik-e, vagy bonyolultabb utat vesz igénybe, mint az ábrán. Harmadszor, és talán váratlanul, a 2. rész végső sebessége nagyobb, mint az 1. részben, de sokkal kevesebb, mint 5,00 m/s.végül vegye figyelembe, hogy a sebesség az út mentén bármilyen magasságban megtalálható, egyszerűen a megfelelő h érték használatával az érdeklődési ponton.

kapcsolatok létrehozása: Take-Home vizsgálat-a potenciál kinetikus energiává történő átalakítása

ebben a kísérletben tanulmányozható a gravitációs potenciális energia kinetikus energiává történő átalakítása. Sima, egyenletes felületen használjon olyan vonalzót, amelynek hossza mentén horony fut, valamint egy könyvet, hogy lejtőt készítsen (lásd az 5.ábrát). Helyezzen egy márványt 10 cm-es helyzetbe a vonalzón, majd hagyja, hogy a vonalzó lefelé gördüljön. Amikor eléri a szintfelületet, mérje meg az egy méter gördítéséhez szükséges időt. Most helyezze a márványt a 20 cm-es, a 30 cm-es pozíciókra, majd mérje meg újra az 1 m-es tekercselés idejét a vízszintes felületen. Keresse meg a márvány sebességét a vízszintes felületen mindhárom pozícióhoz. Telek sebessége négyzetben szemben a megtett távolság a márvány. Mi az egyes telek alakja? Ha az alak egyenes vonal, a cselekmény azt mutatja, hogy a márvány kinetikus energiája alul arányos a felszabadulási ponton lévő potenciális energiájával.

5. ábra. A márvány egy vonalzót gördít le, amelynek sebességét a vízszintes felületen mérik.

koncepcionális kérdések

1. a 2. példában kiszámítottuk egy 20 m magasságú hullámvasút végső sebességét, amelynek kezdeti sebessége 5 m/s lefelé volt. Tegyük fel, hogy a hullámvasút kezdeti sebessége 5 m/s volt felfelé, felfelé gördült, megállt, majd visszafordult egy végső pontra 20 m-rel a rajt alatt. Ebben az esetben azt találjuk, hogy ugyanolyan végső sebességgel rendelkezik. Magyarázza meg az energia megőrzését.
2. a könyvön végzett munka, amikor a polcra emeli, a megtett úttól függ? Időben? A polc magasságában? A könyv tömegén?

problémák & gyakorlatok

1. egy vízerőmű (lásd a 6.ábrát) a gát mögötti víz gravitációs potenciális energiáját elektromos energiává alakítja. a) mi a gravitációs potenciális energia az 50 térfogatú tó generátoraihoz képest.0 km3 (tömeg = 5,00 × 1013 kg), tekintettel arra, hogy a tó átlagos magassága 40,0 m a generátorok felett? b) hasonlítsa össze ezt a 9 megatonnás fúziós bombában tárolt energiával.
   

   6. ábra. Vízerőmű (hitel: Denis Belevich, Wikimedia Commons)

2. (a) mennyi gravitációs potenciális energiát (a talajhoz képest, amelyen épül) tárolnak a Cheops nagy piramisában, mivel tömege körülbelül 7 × 109 kg, tömegközéppontja pedig 36.5 m-rel a környező föld felett? b) hogyan viszonyul ez az energia egy személy napi táplálékfelvételéhez?
3. tegyük fel, hogy egy 350 g-os kookaburra (egy nagy királymadár) felszed egy 75 g-os kígyót, és felemeli 2,5 m-re a Földtől egy ágig. a) mennyi munkát végzett a madár a kígyón? b) mennyi munkát végzett annak érdekében, hogy saját tömegközéppontját az ágra emelje?
4. a 2.példában azt találtuk, hogy a 20, 0 m-es hullámvasút sebessége csak kissé nagyobb volt, ha 5, 00 m / s kezdeti sebessége volt, mint amikor nyugalomból indult. Ez azt jelenti, hogy ΔPE >> KEi. Erősítse meg ezt az állítást azáltal, hogy a ΔPE-t kei-hez viszonyítja. (Vegye figyelembe, hogy a tömeg törlődik.)
5. egy 100 g-os játékautót egy sűrített rugó hajt meg, amely mozgatja. Az autó követi az ívelt pályát a 7. ábrán. Mutassa meg,hogy a játékautó végső sebessége 0,687 m / s, ha kezdeti sebessége 2,00 m / s, és a súrlódás nélküli lejtőn halad, 0,180 m magasságban.
   

   7. ábra. Egy játékautó felfelé mozog egy lejtős pályán. (credit: Leszek Leszczynski, Flickr)

6. egy lesikló sífutásban meglepő módon kevés előny érhető el a futási rajt megszerzésével. (Ez azért van, mert a kezdeti kinetikus energia kicsi, összehasonlítva a gravitációs potenciál energiájának még a kis dombokon elért nyereségével.) Ezt bizonyítja, hogy megtaláljuk a végső sebesség, az időt, egy síelő, aki eget 70.0 m mentén 30 lejtőn elhanyagolása súrlódás: (a) Kezdő a többi. b) 2,50 m/s kezdeti sebességgel kezdve. c) meglep a válasz? Beszéljétek meg, miért még mindig előnyös, hogy a futás kezdete nagyon versenyképes események.

kiválasztott megoldások a problémákra & gyakorlatok

1. a) 1,96 × 1016 J; b) a tóban lévő gravitációs potenciális energia aránya a bombában tárolt energiához 0,52. Vagyis a tóban tárolt energia körülbelül a fele annak, mint egy 9 megatonnás fúziós bombában.

3. a) 1, 8 J; B) 8, 6 J

5. {v} _ {f} = \ sqrt{2gh + {v_0}^2} = \ sqrt{2\bal (9.80 \ text {m / s}^2 \ Jobb) \ Bal (-0.180 \ text{ m}\jobb) + \bal(2.00\text{ m/s} \ jobb)^2} = 0.687 \ text{ m / s} \ \