Ez a szakasz kiterjed:

• Bevezetés Piecewise Funkciók
• Értékelése Piecewise Funkciók
• Grafikus Piecewise Funkciók
• Hogyan Mondd meg, ha egy Piecewise Funkció Folyamatos vagy Nem Folyamatos
• Megszerzése Egyenletek a Piecewise Funkció Grafikonok
• Abszolút Érték, mint egy Piecewise Funkció
• Transzformációk Piecewise Funkciók
• Piecewise Funkció Szót Problémák
• Több Gyakorlat

Piecewise funkciók (vagy darab-bölcs funkciók) azok, aminek a nevük: darab különböző funkciók (al-függvények) minden egy grafikonon. A legegyszerűbb úgy gondolni rájuk, ha egynél több függvényt rajzoltál egy grafikonra, és csak törölted a függvények azon részeit, ahol nem kellene lenniük (a \(x\) ‘ s mentén); ezek különböző időközönként vannak definiálva \(x\). \(y\) másként definiálható a \(x\) különböző értékeihez; a \ (x\) segítségével megvizsgáljuk, hogy milyen intervallumban van, így megtudhatjuk, hogy mi a \(y\).

vegye figyelembe, hogy itt van egy példa egy darabonkénti függvény inverzére a függvények Inverzeiben.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (ennek megjelenítésére más módok is vannak, mint például egy “for” használata “if” helyett, vesszők vagy fél colonok használata az “if”helyett.) Domain: \(\mathbb{R},\,\,\, \ text{or}\,\, \ bal ({- \infty, \ infty } \ jobb)\) tartomány: \(\mathbb{R},\,\,\,\text{or}\,\,\bal( {-\infty ,\infty } \jobb)\)

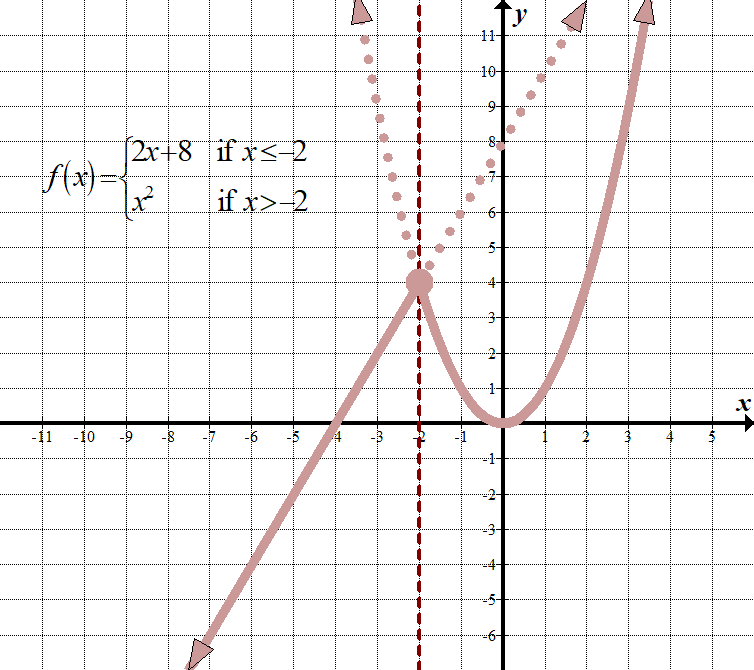Ez azt jelenti, hogy minden \(x\) -2-nél kisebb vagy egyenlő, a \(2x+8\) sort kell grafikonoznunk, mintha ez lenne az Egyetlen függvény a grafikonon. Minden -2-nél nagyobb \(x\) értékhez \({x}^{2}}\) grafikon kell, mintha ez lenne az Egyetlen függvény a grafikonon. Akkor meg kell szabadulnunk azoktól a részektől, amelyekre nincs szükségünk. Ne feledje, hogy továbbra is az Origót használjuk referenciapontként mindkét grafikonhoz!

nézze meg, hogy a \(x=-2\) függőleges vonal hogyan működik “határvonalként” a két gráf között?

vegye figyelembe, hogy a \((-2,4)\) pont zárt körrel rendelkezik rajta. Technikailag csak a \(2x + 8\) függvényhez kell tartoznia, mivel ennek a függvénynek kevesebb vagy egyenlő jele van, de mivel a pont a \({x}^{2}}\) grafikonon is található, csak zárt kört használhatunk, mintha mindkét függvényen megjelenik. Látod, nem olyan rossz, ugye?

értékelve darabonkénti funkciók

néha, akkor kap darabonkénti funkciók, majd kérte, hogy értékelje őket; más szavakkal, keresse meg a\ (y\) értékeket, ha \(x\) értéket kap. Tegyük ezt \(x=-6\) és \(x=4\) (a grafikon használata nélkül). Itt van ismét a függvény:

\(\displaystyle F \ left (x \ right) = \ left \ {\begin {align}2x+8\,\,\,\,\,& \ text{ if }x \ le -2 \ {{x}^{2}}\,\,\,\,\,\,\,\text { }\, & \ text{ if }x > -2\end{align} \right.\)

először a jobb oldali feltételeket szeretnénk megnézni, hogy hol van a \(x\). Amikor \(x = -6\), tudjuk, hogy kevesebb, mint -2, ezért csak a \(x\) – \(2x+8\) – ot csatlakoztatjuk. \(f (x)\) vagy\ (y\) is \((2)(-6)+8=-4\). Nem is érdekel a \ (\boldsymbol{{x}^{2}}\)! Ilyen egyszerű. Azt is láthatja, hogy ezt helyesen csináltuk a fenti grafikon használatával.

most próbálja meg \(x=4\). Először a jobbra nézünk, és látjuk, hogy a \(x\) nagyobb, mint -2, ezért dugjuk be a \({{x}^{2}}\) – Ba. (Ezúttal figyelmen kívül hagyhatjuk a \(2x+8\) értéket.) \ (f (x)\) vagy\ (y\) is \({{4}^{2}}=16\).

darabonkénti függvények ábrázolása

akkor valószínűleg fel kell kérni, hogy grafikon darabonkénti függvények. Néha a grafikonok nem folytonos vagy nem folytonos funkciókat tartalmaznak, ami azt jelenti, hogy rajzolás közben fel kell vennie a ceruzát a grafikon közepén (mint egy ugrás!). A folyamatos funkciók azt jelentik, hogy soha nem kell felvennie a ceruzát, ha balról jobbra húzza őket.

és ne feledje, hogy a gráfok csak akkor valós függvények, ha a függőleges Vonaltesztet teljesítik.

húzzuk meg ezeket a darabonkénti funkciókat, és határozzuk meg, hogy folytonosak vagy nem folytonosak-e. Vegye figyelembe, hogy az egyes funkciókat úgy rajzoljuk, mintha ez lenne az egyetlen, majd “töröljük” azokat a részeket, amelyekre nincs szükség. A tartományt és a tartományt is megkapjuk, mint itt az algebrai függvények részben.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
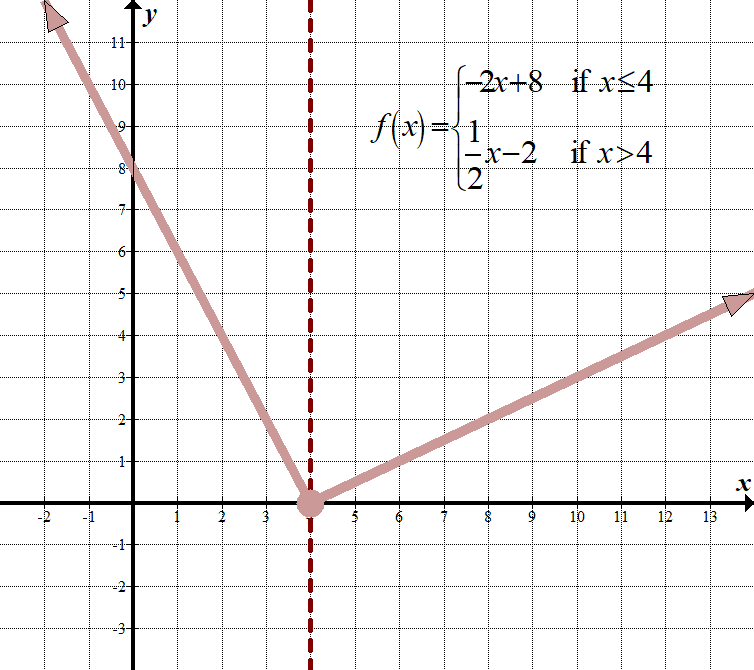\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

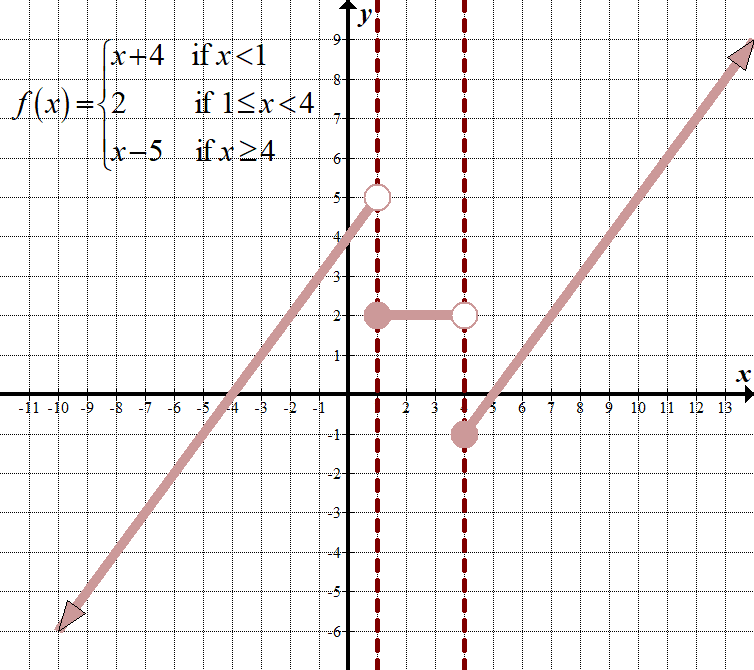We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: Itt a grafikon:

Hogy a piecewise funkció \(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\szöveges{e }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{ha 1 }\le x<4\\-5+x\,\,\,\,\,\szöveges{e }x\a ge 4\end{array} \igaza van.\ ) a számológép, akkor adja meg a funkciót három sorban elosztjuk a függvény minden intervallumban egy “teszt egyenlőtlenség” az intervallum (nézni zárójelben!). az intervallumokkal vagy egyenlőtlenségekkel való felosztás oka az, hogy a számológép 1-et ad vissza, ha az egyenlőtlenség (például \(x<1\)) igaz; például \(((x+4)\) Csak \((x+4)/(1)\) lesz, amikor \(x<1\). Amikor \(x \ ge 1\), Mi elosztjuk 0, így semmi sem fog levonni. Itt van, amit tehetünk a számológép: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {x+4} \right)/\left( {x<1} \right)\\{{Y}_{2}}=\left( 2 \jobbra)/\left( {x\a ge 1\text{ s }x<4} \right)\\{{Y}_{3}}=\left( {-5+x} \right)/\left( {x\a ge 4} \right)\end{array}\) (megjegyzendő, hogy azt is adja meg ezt az egy sort, hogy megszorozzuk a feltételek, ahelyett, hogy elosztjuk a plusz jelek között mind a három funkciók/időközönként: \(\displaystyle {{y}_{1}}}=\left( {x+4} \right)\left( {x<1} \right)+\left( 2 \right)\left( {x\ge 1\text{ and} x<4} \right)+\left( {-5+x} \right)\left( {x\ge 4} \jobb)\).) itt vannak a billentyűleütések három sor használatához. Vegye figyelembe, hogy a 2.matematikát (tesztet) használja a \(\le\), \(\ge\) stb. Például a 2.MATH 6 megkapja a \(\le\) értéket. Használja a 2. matematikát (teszt), a logikához való jogot, majd az 1-et a \ – ban ({{y} _ {2}}\).

Hogyan állapítható meg, hogy a darabonkénti függvény folyamatos vagy nem folyamatos

megnézheti a határpontokat, és megnézheti, hogy a \(y\) pont ugyanaz-e mindegyiknél. (Ha a\(y\)’S más lenne, lenne egy “ugrás” a grafikonon!)

próbáljuk meg ezt a fent használt funkciókhoz:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the “boundary point”: \(\begin{array} {l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) Since \(0=0\), ez a darabonkénti függvény folyamatos.
\(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{ha 1 }\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\szöveges{e }x\a ge 4\end{array} \igaza van.\)	ellenőrizzük a funkció első két részét. Megjegyzés a második részben, \(y\) mindig 2: \(\begin{array} {l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) Since \ (5 \ ne 2\), itt megállhatunk, és megjegyezzük, hogy ez a darabonkénti funkció nem folyamatos. Ha a\(y\)’s egyenlő lenne, akkor el kell mennünk egyet, hogy ellenőrizzük a következő határpontot\(x=4\).

Függvénygráfok egyenleteinek lekérésére lehet kérni, hogy írjon egy darabonkénti függvényt, adott gráfot. Most, hogy tudjuk, milyen darabonkénti funkciók szólnak, ez nem olyan rossz!

az egyenletek lineáris grafikonokból történő előállításának áttekintéséhez lásd: egy vonal egyenleteinek megszerzése, valamint a kvadratikus egyenlet megtalálása pontokból vagy grafikonból.

itt vannak a Grafikonok, magyarázatokkal arról, hogyan lehet levezetni a darabonkénti egyenleteket:

Piecewise Function Graph	Procedure to get Function
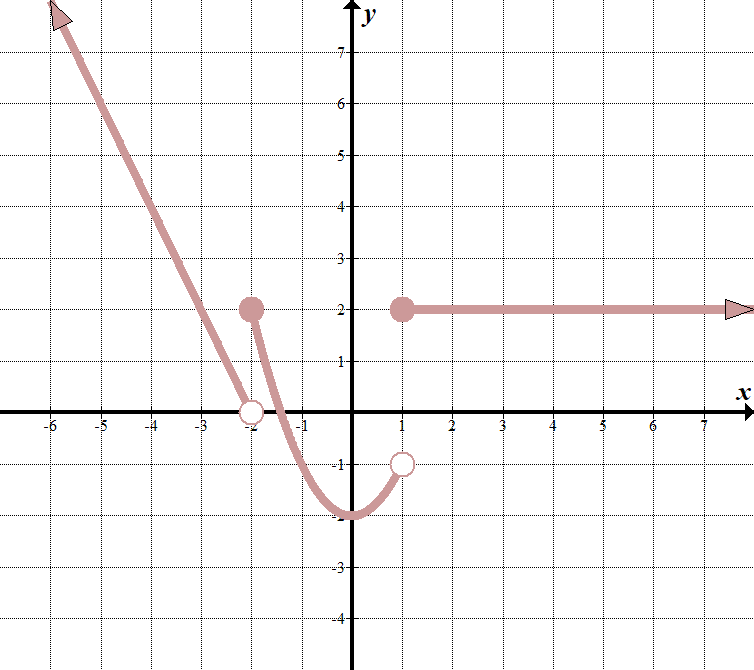	We see that our “boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f \ left (x \ right) = \ left \ {\begin{array}{l} \ text{ }……\,\,\,\,\,\,\,\,\text{if }x <-2 \ \ szöveg{ }……\,\,\,\,\,\,\,\,\text{if }- \ text{2} \ Le x <1 \ \ \ text{ }……\,\,\,\,\,\,\,\,\text{if }x \ ge 1 \ end{array} \ right.\) választhatunk két pontot \((-2,0)\) és \((-3,2)\) a bal szélső sorban, hogy megkapjuk az egyenletet \(y=-2x-4\). a középső függvény \(y = {x}^{2}}-2\), A jobb szélső funkció csak a vízszintes vonal \(y=2\). így a darabonkénti függvény: \(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}-2x-4\,\,\,\,\,\,\,\szöveges{e }x<-2\\\text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\szöveges{e }-\text{2}\le x<1\\\szöveget{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }x\a ge 1\end{array} \igaza van.\)
	látjuk, hogy “határvonalunk” \(x=5\). Mivel a sorok a \((5,4)\) – nál találkoznak, nem számít, hogy hova helyezzük a \(\le \) vagy \(\ge \) jelet; csak nem tudjuk mindkét helyre tenni, különben nem lenne funkció. Eddig: \(\displaystyle F\left( x \ right)= \ left \ {\begin{array}{l} \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x <5 \ \ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x \ ge 5 \ end{array} \ right.\) ismét meg kell vizsgálnunk az egyes sorokat külön-külön, hogy meghatározzuk egyenleteiket. Mindkét sorból 2 pontot vehetünk el, hogy ezeket megkapjuk, vagy lejtőkből és \(y\)–elfogásokból származhatunk; a darabonkénti funkció: \(\displaystyle F\left( x \ right) = \ left \ {\begin{array}{l} \ frac{6}{5}x-2\,\,\,\,\,\,\,\{if }x<5 \ \ \ frac{2}{5}x+2\,\,\,\,\,\,\,\text{if }x \ ge 5 \ end{array} \ right.\)

abszolút érték, mint egy darabonkénti függvény

abszolút értékfüggvényeket írhatunk darabonként – ez nagyon jó! Érdemes lehet áttekinteni az abszolút Értékegyenletek és egyenlőtlenségek megoldását, mielőtt folytatná ezt a témát.

tegyük fel, hogy megvan a \(f\bal( x \jobb)=\bal| x \jobb|\) függvény. Abból, amit korábban megtanultunk, tudjuk, hogy amikor\ (x\) pozitív, mivel az abszolút értéket vesszük, akkor is csak \(x\) lesz. De ha\ (x\) negatív, amikor az abszolút értéket vesszük, akkor az ellenkezőjét kell vennünk (negálni), mivel az abszolút értéknek pozitívnak kell lennie. Van értelme? Tehát például, ha volt \(|5|\), akkor csak azt vesszük, ami az abszolút jelben van, mivel pozitív. De a \(/-5/\) esetében az abszolút érték belsejében lévő ellentétes (negatív) értéket kell figyelembe vennünk ahhoz, hogy \(\displaystyle 5\,\,\,(-\,-5=5)\).

Ez azt jelenti, hogy ezt az abszolút értékfüggvényt darabonként írhatjuk. Figyeljük meg, hogy mi lehet kapni a “fordulópont” vagy “határpont” beállításával bármi van benne az abszolút érték 0. Ezután vagy az eredeti funkciót használjuk, vagy elutasítjuk a funkciót, attól függően, hogy a függvény jele (abszolút érték nélkül) ebben az intervallumban van-e.

például írhatunk \(\displaystyle \ left / x \ right / \ text { } = \ left \ {\begin {array}{L}x\,\,\,\,\,\,\,\,\,\szöveg{if }x\ge 0 \ – x\,\,\,\,\,\text{if }x<0\end{array} \right.\). Azt is vegye figyelembe, hogy ha a funkció folyamatos (nincs “ugrás”) a határponton, akkor nem számít, hol helyezzük el a “kisebb vagy egyenlő” (vagy “nagyobb vagy egyenlő”) jeleket, mindaddig, amíg nem ismételjük meg őket! Nem ismételhetjük meg őket, mert elméletileg nem lehet két értéke \(y\) ugyanarra a \(x\) értékre, vagy nem lenne függvényünk.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the “boundary line”. Ezt úgy végezzük, hogy az abszolút érték belsejében 0-ra állítjuk, majd megoldjuk a \(\boldsymbol{x}\) értéket. amikor \(2x+3\ge 0\), megkapjuk \(\displaystyle x\ge -\frac{3}{2}\) (valójában megtarthatjuk a \ (\ge\), amikor megoldjuk). Ha a \(2x+3\) pozitív, akkor csak “ahogy van”, de ha negatív, akkor az egészet el kell utasítanunk. ezért a darabonkénti függvény: \(\displaystyle \ left / {2x + 3} \ right / = \ left \ {\begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{if }x \ ge- \frac{3}{2} \text {} \ \ – 2x-3\,\,\,\,\,\text{if }x<-\frac{3}{2}\end{array} \right.\) próbáld ki-működik!
\(F \ left (x \ right)=\left| {{{x}^{2}}}} -4}\right|\)	először keressük meg a “határvonal(ok)”; az abszolút értéken belüli értéket 0-ra állítjuk. amikor \ ({{x}^{2}}-4 \ ge 0\), kapunk \(x\le -2\) vagy \(x\ge 2\) (próbáljon ki néhány számot!). Ha\ ({x}^{2}}-4\) pozitív, akkor csak “ahogy van”, de ha negatív, akkor meg kell tagadnunk. A piecewise funkció: \(\displaystyle \balra| {{{x}^{2}}-4} \right|=\maradt\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\szöveges{e }x\le -2\\4-{{x}^{2}}\,\,\,\,\,\szöveges{e }-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\szöveges{e }x\a ge 2\text{ }\end{array} \igaza van.\ ) vagy \(\displaystyle \left / {{{x}^{2}}-4} \ right / = \ left \ {\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\text{if }x \ le -2 \ text { }\,\, \ text{or}\,\, \ text{ }x \ ge 2 \ \4 – {x}^{2}}\,\,\,\,\,\,\,\text{if }-2<x<2\end{array} \right.\) ismét (mivel a függvény folyamatos), tényleg nem számít, hol van a \(\le\) és \(\ge \) (szemben a \(<\) és \(>\)), mindaddig, amíg nem ismételjük meg őket.
\(F\left( x \right)=2x+\left| {x+2} \right|\)	ez egy kicsit trükkösebb, mivel az abszolút értéken belül és kívül van egy \(x\). A “határvonal” esetében Csak azt használjuk, ami az abszolút értéken belül van. amikor \(x + 2 \ ge 0\), kapunk \(x\ge -2\). De a darabonkénti funkcióhoz az egész funkciót kell használnunk, beleértve az abszolút értéken kívüli részt is. Tehát a darabonkénti funkció: \(\displaystyle 2x + \ left / {x + 2} \ right / = \ left \ {\begin{array}{l}2x + x+2\,\,\,\,\,\{if }X\ge -2 \ \ 2x-x-2\,\,\,\,\,\text{if }x<-2\end{array} \right.\) egyszerűsítsük: \(\displaystyle 2x + \ left / {x + 2} \ right / = \ left \ {\begin{array}{l}3x+2\,\,\,\,\,\,\,\{if }X \ ge -2 \ \ x-2\,\,\,\,\,\,\,\,\,\,\text{if }x<-2\end{array} \right.\) próbáljon ki néhány értéket kevesebb, mint akkor -2; működniük kell!
\(g\left( x \right)=\left| {{{x}^{2}}}-4x-5} \right|\)	ez a legjobban egy jeldiagrammal oldható meg, mivel kvadratikus, és tudnunk kell, hogy hol pozitív a függvény és negatív. először a kvadratikus értéket az abszolút értékfüggvényen belül \(\bal( {x-5} \jobb)\bal( {x+1} \jobb)\). Ezután egy jel diagram, hogy hol a tényezők pozitív és negatív, és ne feledje, hogy ahol a tényezők pozitívak, használjuk a funkciót “ahogy van”, és ahol a tényezők negatívak, akkor tagadja a funkciót: \(\displaystyle \balra| {{{x}^{2}}-4x-5} \right|=\maradt\{ \begin{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }x\le -1\,\,\,\,\szöveges {, vagy}\,\,\,\x\a ge 5\\-\left( {{{x}^{2}}-4x-5} \jobbra)\,\,\,\,\szöveges{e }-1<x<5\text{ }\end{array} \igaza van.\)
\(\displaystyle g\left( x \right)=\FRAC {\left| {x+2} \right|}} {{{x+2}}}}\)	ez egy racionális függvény, mivel van egy változó a nevezőben. amikor \(x + 2 \ ge 0\), kapunk \(\displaystyle x \ ge -2\). Ha\ (x+2\) pozitív, akkor csak “ahogy van”, de ha negatív, akkor meg kell tagadnunk az abszolút értéket: \(\displaystyle \ frac {{\left / {x + 2} \ right/}} {{x + 2}}}} = \ bal \ {array} {l} \ frac{{x + 2}}{{x+2}}\,\,\,\,\,\,\,\,\,\szöveg{if }x \ ge -2 \ \ frac {{- x-2}}{{x+2}}\,\,\,\,\,\,\text{if }x<-2\end{array} \right.\). De óvatosnak kell lennünk, mivel \(x\ne 2\) (domain korlátozás: a nevező 0 lenne). ezért a darabonkénti függvény: \(\displaystyle \ frac {{\left / {x + 2} \ right/}} {{x + 2}}}} = \ left \ {begin {array} {l}1\,\,\,\,\,\,\,\,\,\,\text{if }x>-2\\-1\,\,\,\,\,\,\text{if }x<-2\end{array} \right.\).

:

Absolute Value Graph	Method to get Piecewise Function
	We see that our “boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Ez azért van, mert ahhoz, hogy a határvonalat abszolút értékfüggvénnyel kapjuk meg, az abszolút értéken belüli értéket 0-ra állítjuk, a \(x\) értéket pedig megoldjuk. amikor \ (x >0\), láthatjuk, hogy a vonal egyenlete \(y=2x-2\). Amikor \(x <0\), az egyenlet \(y = 2x-2\). Ezt darabonként írhatjuk: \(\displaystyle F \ left (x \ right)= \ left \ {\begin{array} {l}2x-2\,\,\,\,\,\,\,\text{if }x>0\\-2x-2\,\,\,\text{if }x\le 0\end{array} \right.\) ezt transzformált abszolút értékfüggvényként is írhatjuk: \(y = 2 \ bal / x\ jobb|-2\) vagy \(y= \ bal / {2x} \ jobb / -2\) (mivel 2 pozitív, a \(\bal| {\,\,} \jobb|\) belsejében vagy kívül lehet). (Ennek van értelme, mivel amikor a \(\left| { \ ,\,} \right|\) belsejében van \(> 0\), akkor a \(y=2x-2\) szabályos függvényt használjuk, és amikor a belsejében van \(< 0\), akkor negáljuk az abszolút érték részt, hogy \(y=-\bal( {2x} \jobb)-2\)).
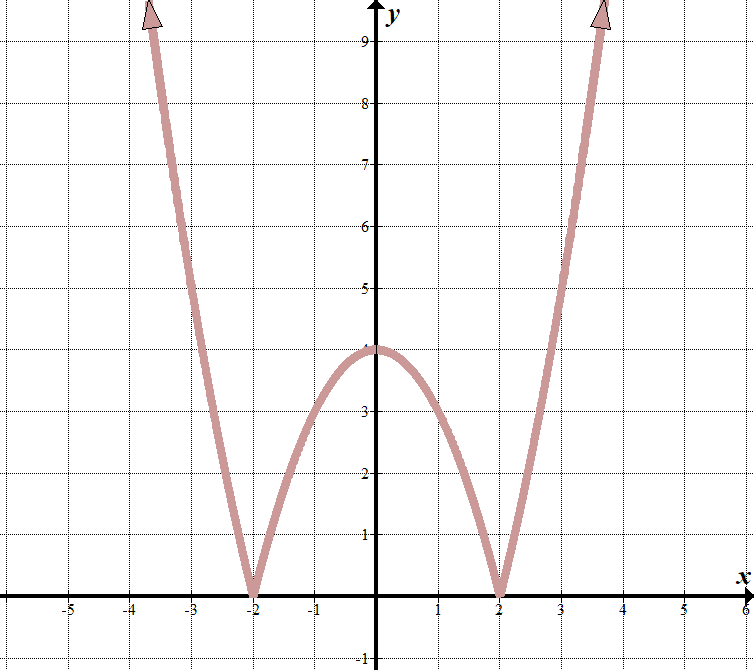	látjuk, hogy “határvonalaink” \(x=2\) és \(x=-2\), tehát az abszolút értékjelen belül tényezőknek kell lenniük a \(x-2\) és \(x+2\). amikor \ (x <-2\) vagy \(x>2\), láthatjuk, hogy a grafikon úgy néz ki, mint a grafikon normál része \(y = {x}^{2}}-4\). (Ezt a tényezők ismeretében találtam ki, és jól tippeltem!) Amikor \(-2<x<2\), az egyenletet megfordítják, vagy negálják (átfordítva a \(x\)-tengely). Ezt darabonként írhatjuk: \(\displaystyle F \ left (x \ right)= \ left \ {\begin{array} {L} {x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{if }x <-2 \ text{ or }x >2\ – {{x}^{2}}}} \ text{+ 4}\,\,\,\,\,\,\text{if }-2 \ le x \ le 2 \ end{array} \ right.\) láthatjuk, hogy ez egy átalakított kvadratikus függvény \(y={x}^{2}}} -4\) indult, abszolút értékkel körülötte, mivel minden \(y\) érték pozitív: \(y=\bal| {{{{x}^{2}}} -4} \jobb|\).
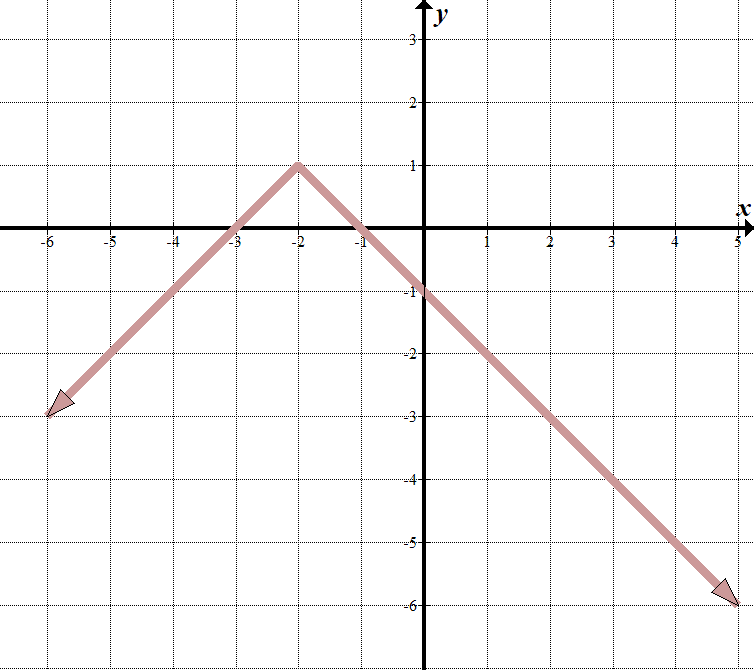	látjuk, hogy” határvonalunk ” \(x=-2\), tehát az abszolút értékjel belsejében \(x+2\) kell lennie. amikor \ (x >-2\), láthatjuk, hogy a vonal egyenlete \(y=-x-1\). Amikor \(x <-2\), a sor \(y=x+3\). Ezt darabonként írhatjuk: \(\displaystyle F \ left (x \ right)= \ left \ {\begin{array}{L} – x-1\,\,\,\,\,\,\text{if }x>-2 \ \ x+3\,\,\,\,\,\,\,\,\,\,\text{if }x \ le -2 \ end{array} \ right.\) valószínűleg könnyebb ezt transzformált abszolút értékfüggvényként írni. Láthatjuk, hogy a szülő abszolút értékfüggvény függőlegesen van megfordítva, balra mozog 2, majd felfelé 1. Abszolút érték egyenletünk \(y = – \ bal / {x + 2} \ jobb|\,\,+\,\,1\). Ez ugyanaz, mint a fenti darabonkénti funkció. Próbáld ki – működik!

A darabonkénti függvények transzformációi

egy darabonkénti függvény átalakítását végezzük. A Szülőfüggvényekről és azok Átalakításairól itt, a Szülőgráfok és transzformációk részben tájékozódhatunk. Valószínűleg először el akarja olvasni ezt a részt, mielőtt megpróbálna egy darabonkénti átalakítást.

alakítsuk át a következő darabonkénti függvényt, amely a \(x\) tengely körül forog, függőlegesen nyújtva 2 egységgel, 1 egységgel jobbra, 3 egységgel felfelé.

levonja \(-2f\left( x-1 \jobbra)+3\), ahol:

\(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\text{ e }x<&\text{ ha 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ e }x\a ge 4\end{align} \igaza van.\)

győződjünk meg róla, hogy a “határ” pontokat használjuk, amikor kitöltjük az átalakulás t-diagramját. Ne feledje, hogy a zárójelben lévő transzformációk a \(x\) – ra (az ellenkező matematikát), a külső pedig a \(y\) – ra kerülnek. A T-diagram elkészítéséhez, amint az az alábbi táblázatban látható, kulcsfontosságú pontokat használhatunk, köztük két pontot az egyes “határvonalakon”.

vegye figyelembe, hogy mivel ez az átalakulás bonyolult, új darabonkénti funkcióval tudunk előállni a 3 “darab” átalakításával, valamint a “\(x\)”s átalakításával, ahol a határpontok vannak (1 hozzáadásával vagy jobbra haladva 1), mivel a “\(x\)”s ellentétes matematikát végzünk. Ahhoz, hogy az új funkciókat minden intervallumban megkapjuk, az eredeti egyenletben csak “\(x-1\)” helyettesíthetjük “\(x\)”, szorozzuk meg -2-vel, majd adjunk hozzá 3-at. Például:\(\displaystyle-2F \ left ({x-1} \ right)+3 = -2 \ left + 3 = -2 \ left ({x+3} \right)+3=-2x-3\).

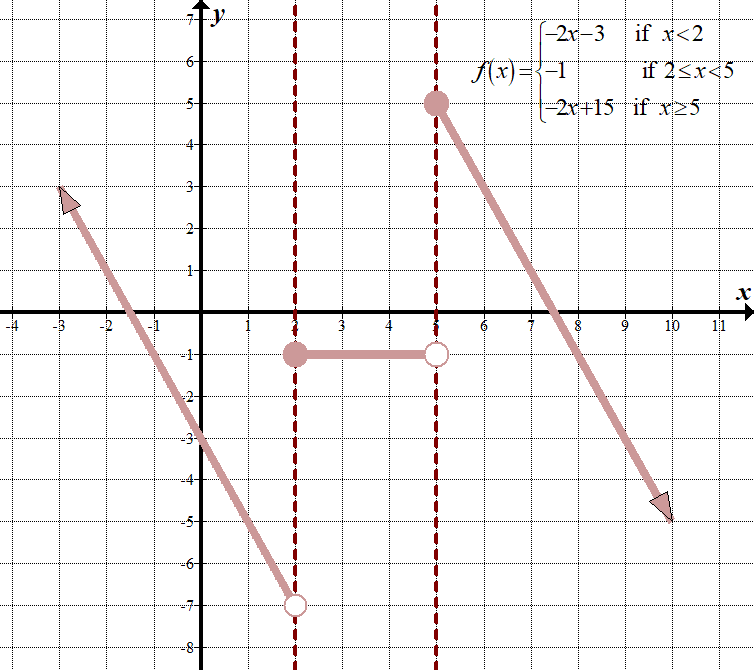
\(\displaystyle -2f\left( {x-1} \right)+3=\maradt\{ \begin{array}{l}-2\left( {\left( {x-1} \right)+4} \right)+3=2x-3,\,\,\,\,\szöveges{ e }x-1<1\,\,\,\left( {x<2} \right)\\-2\left( 2 \jobbra)+3=-1,\,\,\,\,\szöveges{ e }\,\text{ 2 }\le x<5\\-2\left( {\left( {x-1} \right)-5} \right)+3=2x+15,\,\,\,\,\szöveges{ e }x\a ge 5\end{array} \igaza van.\)

itt vannak az “előtte ” és” utána ” grafikonok, beleértve a t-diagramot:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

kedvenc kutyatartója a kutya súlyának megfelelően számít. Ha a kutya 15 font alatt, a groomer díjak $35. Ha a kutyád 15-40 font között van, akkor 40 dollárt számít fel. Ha a kutya több mint 40 font, ő díjak $40, plusz egy további $2 minden Font.

(a) írjon egy darabonkénti függvényt, amely leírja, hogy a kutya groomer díjak.

(b) Gráfolja a függvényt.

(c) Mi lenne a groomer díj, ha aranyos kutyája súlya 60 font?

megoldás:

(a) látjuk, hogy a “határpontok” 15 és 40, mivel ezek azok a súlyok, ahol az árak változnak. Mivel két határpontunk van, három egyenlet lesz a darabonkénti függvényünkben. Meg kell kezdeni 0, mivel a kutyák súlya több mint 0 Font:

\(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}\szöveget{ }……\,\,\,\,\,\,\,\,\,\szöveges{e }0<x\le 15\\\szöveget{ }……\,\,\,\,\,\,\,\,\,\szöveges{e }15<x\le 40\\\szöveget{ }……\,\,\,\,\,\,\,\,\,\szöveges{e }x>40\end{array} \igaza van.\)

keressük a ” válaszokat “(mennyibe kerül a ápolás) a” kérdésekre ” (mennyi a kutya súlya) a három árkategóriára. Az első kettő csak lapos díjak (35 dollár, illetve 40 dollár). Az utolsó egyenlet egy kicsit trükkösebb; a groomer díjak $40 plusz $2 minden font felett 40. Próbáljuk meg a valós számokat:ha a kutya súlya 60 font, ő fog díjat $40 plusz $2 alkalommal \(20 (60-40)\). Ezt egyenletgé alakítjuk: \(40+2(x–40)\), amely egyszerűsíti a \(2x–40\) értéket (lásd, hogyan 2 a lejtő?).

az egész darabonkénti függvény:

\(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}\szöveget{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }0<x\le 15\\\szöveget{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }15<x\le 40\\\text{ }40+2\left( {x-40} \jobbra)\,\,\,\,\,\,\szöveges{e }x>40\end{array} \igaza van.\) vagy \(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}\szöveget{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }0<x\le 15\\\szöveget{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }15<x\le 40\\\text{ }2x-40\,\,\,\,\,\,\,\szöveges{e }x>40\end{array} \igaza van.\)

(b) Let ‘ s graph:ne feledje, hogy ez a darabonkénti egyenlet nem folyamatos. Szintén vegye figyelembe, hogy a probléma ésszerű tartománya lehet \(\bal ({0,200} \ jobb]\) (mivel a kutyák nem súlya meghaladja a 200 fontot!) és egy ésszerű tartomány lehet \(\left \ cup \ left\).

(c) ha a kutya súlya 60 font, akkor vagy használja a grafikon, vagy a funkció, hogy látni, hogy meg kell fizetni $80. Whoa! Ez többe kerül, mint egy emberi hajvágás (legalább a hajvágásom)!

probléma:

azt tervezi, hogy eladja szereti a matematikai pólókat adománygyűjtőként. A nagykereskedelmi pólóvállalat 10 dollárt számít fel egy ingért az első 75 ingért. Az első 75 ing után legfeljebb 150 inget vásárol, a vállalat ingenként 7, 50 dollárra csökkenti az árát. Miután 150 inget vásárolt, az ár ingenként 5 dollárra csökken. Írjon egy olyan funkciót, amely modellezi ezt a helyzetet.

megoldás:

látjuk, hogy a” határpontok ” 75 és 150, mivel ezek a vásárolt pólók száma, ahol az árak változnak. Mivel két határpontunk van, három egyenlet lesz a darabonkénti függvényünkben. Kezdjük a \(x \ ge 1\), mivel feltételezzük, hogy legalább egy inget vásárolnak. Ebben a problémában vegye figyelembe, hogy a vásárolt pólók (\(x\)) vagy a tartomány egész számnak kell lennie, de ez a korlátozás nem befolyásolhatja a probléma kimenetelét.

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text {}……… \text{ if }1\Le x\le 75\\\text {}………. \text{ if }75<x\le 150\\\Text {}…… \Text{ if }X>150\end{array} \right.\)

keressük a” válaszokat “(pólók teljes költsége) a” kérdésekre ” (hány vásárolt) a három árkategóriára.

legfeljebb 75 ing esetén az ár 10 dollár, tehát a teljes ár \(10x\). Több mint 75 ing, de akár 100 ing esetében a költség 7,50 dollár, de az első 75 póló továbbra is 10 dollárba kerül ingenként. A második funkció magában foglalja az első 75 ingre költött 750 dollárt (75-szer $10), valamint a 75 feletti ingek számának 7,50-szeresét is, ami \((x-75)\) lenne. Például, ha 80 inget vásárolt, akkor \ (\$10\times 75=\$750\), plusz \(\$7.50 \ times 5\,\) (80 – 75) az ingek után a 75.ing.

hasonlóképpen, több mint 150 ingért továbbra is fizetnénk a $10 árat 75 ingen keresztül, a $ 7.50 ár 76 nak nek 150 ing (75 több ing), majd $ 5 per ing száma ing vásárolt több mint 150. Fizetünk \(10(75)+7.50(75)+5(x-150)\) A \ (x\) ingek. Tedd be a számokat, és próbáld ki!

Az egész piecewise funkció:

\(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }1\le x\a le 75\\\text{ }7,5 x\text{ }+\szöveget{ }187.5\,\,\,\,\,\szöveges{ha 7}5<x\150 le\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if }x>150 \ end{array} \ right.\) vagy \(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }1\le x\a le 75\\\text{ }7,5 x\text{ }+\szöveget{ }187.5\,\,\,\,\,\szöveges{ha 7}5<x\150 le\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }x>150\end{array} \igaza van.\)

probléma:

egy buszjárat 50 dollárba kerül az első 400 mérföldnél, minden további 300 mérföld (vagy annak egy része) pedig 10 dollárt ad a viteldíjhoz.

használjon darabonkénti funkciót, hogy képviselje a busz viteldíját a mérföldben kifejezett távolság szempontjából.

megoldás:

Ez valójában trükkös probléma, de először gondoljunk először a “határpontra”, amely 400. Ez elég egyszerű, ha az út kevesebb, mint 400 mérföld; a költség $50.

nagyobb, mint 400 mérföld, van, hogy vonjuk ki az első 400 mérföld (de ne feledje, hogy tartalmazza az első $50), szakadék, hány mérföldet hagyott 300 mérföld (- körbe, ha van egy tört összeg), majd szorozza meg, hogy a $10.

a trükkös rész az, amikor “kerekítjük” a következő 300 mérföld egy részét. Használhatunk “plafon” funkciót (a \(\bal\lceil {} \rceil\) jelöli); ez a függvény a legkisebb egész számot adja, amely nagyobb vagy egyenlő a bemenetével; például mind a 3.5, mind a 4 felső határa 4.

így van ez:

\(\displaystyle f\left( x \jobbra)=\maradt\{ \begin{array}{l}\text{ }50\szöveget{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\szöveges{e }0\le x\le 400\\\text{ }50+10\times \maradt\lceil {\frac{{x-400}}{{300}}} \igaz\rceil \szöveget{ }\,\,\,\,\,\,\szöveges{ e }x>400\end{array} \igaza van.\)

próbáljuk meg! Ha van egy 1500 mérföldes út, a költség lenne \(\displaystyle 50 + 10 \ times \ bal \ lceil {\frac{{1500-400}}{{300}}} \jobb\rceil \text{ }=50+10\times 4=\$90\).

probléma:

milyen értéke \(\boldsymbol{a}\) tenné ezt darabonkénti függvény folyamatos?

\(\displaystyle F \ left (x \right) = \ left \ {\begin{array}{l}3 {x}^{2}}+4\,\,\,\,\,\text{ if }x<-2\\5x+\boldsymbol{a}\,\,\,\,\,\,\,\,\text{if }x \ ge -2 \ end{array} \ right.\)

megoldás:

ahhoz, hogy a darabonkénti függvény folytonos legyen, a határpontnál (ahol a függvény megváltozik) a két \(y\) értéknek azonosnak kell lennie. Tudjuk csatlakoztatni a -2 a \(x\), mind a funkciókat, hogy a \(i\)’s ugyanaz

a\(\begin{align}3{{x}^{2}}+4&=5x+egy\\3{{\left( {-2} \jobbra)}^{2}}+4&=5\left( {-2} \right)+egy\\12+4&=-10+egy\\&=26\end{align}\)

Ha a \(a=26\), a piecewise funkció folyamatos!

Ismerje meg ezeket a szabályokat, gyakoroljon, gyakoroljon, gyakoroljon!

további gyakorlat: az alábbi Mathway widget segítségével próbáljon meg írni egy darabonkénti funkciót. Kattintson a Küldés (a probléma jobb oldalán található kék nyíl) elemre, majd kattintson az abszolút érték darabonkénti írása gombra a válasz megtekintéséhez.

beírhatja a saját problémáját is, vagy kattintson a jobb felső sarokban lévő három pontra, majd kattintson a “példák” gombra a téma szerinti fúráshoz.

Ha rákattint a Tap gombra a lépések megtekintéséhez, vagy kattintson ide, regisztrálhat a Mathway-en egy ingyenes próbaverzióhoz, majd bármikor frissíthet fizetett előfizetésre (bármilyen típusú matematikai probléma megoldásához!).

tovább a mátrixokra és megoldási rendszerekre mátrixokkal-készen állsz!