Algebra nagyon szórakoztató-kapsz rejtvényeket megoldani!
A Puzzle
mi a hiányzó szám?
| − | 2 | 4 |
ok, a válasz 6, ugye? Mert 6-2 = 4. Könnyű dolog.
Nos, az algebrában nem használunk üres dobozokat, hanem betűt használunk (általában x vagy y, de minden betű rendben van). Tehát írunk:
| x | − | 2 | = | 4 |
Ez tényleg ilyen egyszerű. A levél (ebben az esetben egy x) csak azt jelenti, hogy “ezt még nem tudjuk”, gyakran ismeretlennek vagy változónak nevezik.
és amikor megoldjuk, írunk:
| x | = | 6 |
Why Use a Letter?
| Because: | |
| it is easier to write “x” than drawing empty boxes (and easier to say “x” than “the empty box”). | |
| ha több üres doboz van (több “Ismeretlen”) mindegyikhez más betűt használhatunk. |
tehát x egyszerűen jobb, mint egy üres doboz. Nem próbálunk szavakat csinálni vele!
és nem kell x-nek lennie, lehet y vagy w … vagy bármilyen betű vagy szimbólum tetszik.
hogyan lehet megoldani
az Algebra olyan, mint egy puzzle, ahol valami “x − 2 = 4” – vel kezdjük, és valami olyasmivel akarunk végezni, mint “x = 6”.
de ahelyett, hogy azt mondaná, hogy “nyilvánvalóan x = 6”, használja ezt a ügyes lépésről-lépésre megközelítést:
- dolgozza ki, mit kell eltávolítani, hogy ” x = …”
- távolítsa el az ellenkezőjét (a Hozzáadás a kivonás ellentéte)
- tegye ezt mindkét oldalra
itt van egy példa:
eltávolítani
a “-2”
![]()
eltávolításához tegye
az ellenkezőjét, ebben az esetben adjunk hozzá 2
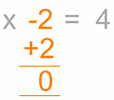 /div>
/div>
csináld
mindkét oldal
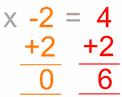
melyik …
![]()
![]()
miért adtunk hozzá 2-t mindkét oldalhoz?
az “egyensúly megtartása”…
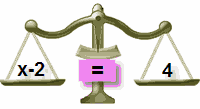
Add 2 to Left Side

kiegyensúlyozatlan!
Add 2 A jobb oldalon is
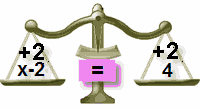
csak emlékezz erre:
az egyensúly megtartása érdekében, amit a “=”
egyik oldalával teszünk, a másik oldalnak is meg kell tennünk!
See this in action at the Algebra Balance Animation.
Another Puzzle
Solve this one:
| x | + | 5 | = | 12 |
What we want is an answer like “x = …”,
but the +5 is in the way of that!
lemondhatjuk a +5, -5 (mert 5-5=0)
próbálja ki magát
most gyakorolja ezt az egyszerű Algebra munkalapot, majd ellenőrizze a válaszokat. Próbálja meg használni az itt bemutatott lépéseket, ahelyett, hogy csak kitalálná!
próbálja ki az alábbi kérdéseket, majd olvassa el az Algebra – szorzás bevezetését