a koordináta sík
tanulási cél(ok)
· rajz rendezett párokat egy koordináta síkon.
· rendezett pár esetén határozza meg kvadránsát.
Bevezetés
a koordináta síkját évszázadokkal ezelőtt fejlesztették ki, és René Descartes francia matematikus finomította. Tiszteletére a rendszert néha derékszögű koordinátarendszernek nevezik. A koordinátasíkot pontok és gráfvonalak ábrázolására lehet használni. Ez a rendszer lehetővé teszi számunkra, hogy leírjuk az algebrai kapcsolatokat vizuális értelemben, valamint segít létrehozni és értelmezni az algebrai fogalmakat.
Ismerkedés a koordináta sík
akkor valószínűleg használt koordináta sík előtt. Például használt már valaha rácsos átfedést egy objektum helyzetének feltérképezésére? (Ez gyakran történik útitervek is.)

Ez a “térkép” vízszintes és függőleges rácsot használ az objektum helyére vonatkozó információk továbbítására. Vegye figyelembe, hogy az A-F betűk a tetején vannak felsorolva, az 1-6 számok pedig a bal szél mentén vannak felsorolva. A térkép bármely elemének általános helyét a rács négyzetének betűjével és számával lehet megtalálni. Például megtalálhatja a ” 4F ” négyzetben létező elemet úgy, hogy ujját a vízszintes mentén F betűre mozgatja, majd egyenesen lefelé, így összhangban van a 4-gyel. A térképen egy kék lemez található ezen a helyen.
a koordináta síkja hasonló elemekkel rendelkezik, mint a fent látható rács. Vízszintes tengelyből és függőleges tengelyből áll, derékszögben metsző vonalak száma. (Merőlegesek egymásra.)
a koordináta sík vízszintes tengelyét x tengelynek nevezzük. A függőleges tengelyt y tengelynek nevezik. Az a pont, ahol a két tengely metszi az Origót. Az eredet az x tengelyen 0, az y tengelyen 0.
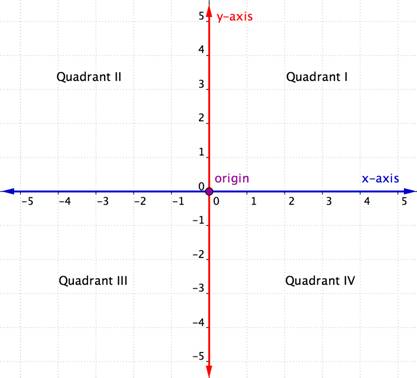
a metsző x – és y-tengelyek a koordinátasíkot négy részre osztják. Ezt a négy szakaszt kvadránsnak nevezik. A kvadránsokat az I., II., III. és IV. római számokkal nevezték el, kezdve a jobb felső kvadránssal és az óramutató járásával ellentétes irányban haladva.
a koordinátasíkon lévő helyeket rendezett párként írják le. Egy rendezett pár jelzi a pont helyét azáltal, hogy a pont helyét az x tengely mentén (a megrendelt pár első értéke), valamint az y tengely mentén (a megrendelt pár második értéke) határozza meg.
egy rendezett párban, például (x, y), az első értéket x-koordinátának, a második értéket pedig y-koordinátának nevezzük. Vegye figyelembe, hogy az x-koordináta az y-koordináta előtt szerepel. Mivel az eredet x-koordinátája 0, y-koordinátája 0, a rendezett párja meg van írva (0, 0).
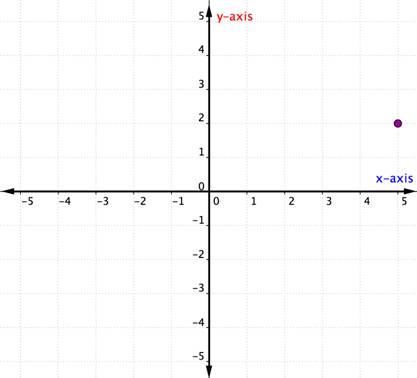
vegye figyelembe az alábbi pontot.
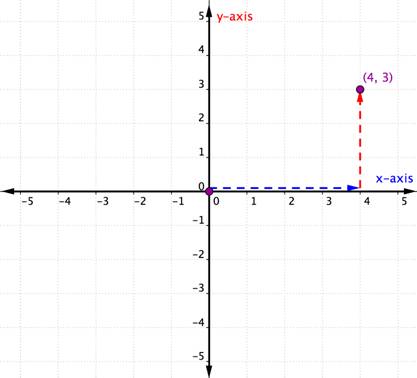
a pont helyének azonosításához kezdje a származást (0, 0), majd jobbra haladjon az x tengely mentén, amíg a pont alá nem kerül. Nézd meg az X tengely címkéjét. A 4 azt jelzi, hogy az eredetből négy egységet utazott jobbra az x tengely mentén. Ez az x-koordináta, az első szám a megrendelt párban.
4-től az x-tengelyen mozgassa fel a pontot, és vegye észre azt a számot, amellyel az y tengelyre igazodik. A 3 azt jelzi, hogy az x tengely elhagyása után 3 egységet felfelé haladtál függőleges irányban, az y tengely irányában. Ez a szám az y-koordináta, a második szám a megrendelt párban. 4-es x-koordinátával és 3-as y-koordinátával a megrendelt pár (4, 3).
nézzünk egy másik példát.
|
Example |
||
|
Problem |
Describe the point shown as an ordered pair. |
|
|
|
||
|
(5, y) |
– kor Kezdődik, a származás, majd mozgassa az x-tengely mentén. Ez az x-koordináta, amelyet először a rendezett párban írnak. |
|
|
(5, 2) |
lépjen 5-ről a megrendelt párra, majd olvassa el a számot az Y tengelyen. Ez az y-koordináta, a második a megrendelt párban. |
|
|
válasz |
a rendezett párként megjelenített pont (5, 2). |
|
most, hogy tudod, hogyan kell használni az X – és Y-tengelyek, akkor a telek egy rendezett pár is. Ne feledje, hogy mindkét folyamat az eredetnél kezdődik-az elején! A következő példa azt mutatja, hogyan kell ábrázolni a megrendelt párt (1, 3).
|
Example |
||
|
Problem |
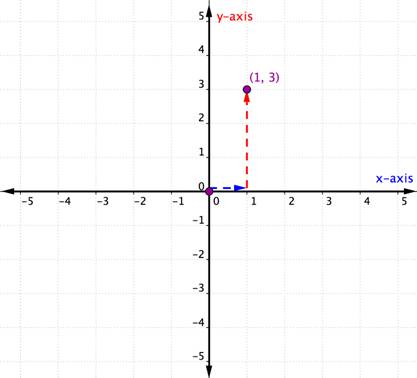
Plot the point (1, 3). |
|
|
|
||
|
The x-coordinate is 1 because it comes first in the ordered pair. Kezdje az eredetnél, és mozgassa az 1 egység távolságát pozitív irányban (jobbra) az eredettől az x tengely mentén. |
az y-koordináta 3, mert a második a megrendelt párban. Innen mozogjon közvetlenül 3 egység pozitív irányba (felfelé). Ha az y tengelyre néz, akkor a tengelyen 3-mal kell felsorolni. |
|
|
válasz |
rajzoljon egy pontot ezen a helyen, és jelölje meg a pontot (1, 3). |
|
az előző példában mind az x -, mind az y-koordináták pozitívak voltak. Ha egy rendezett pár koordinátáinak egyik (vagy mindkettő) negatív, akkor egy vagy mindkét tengely mentén negatív irányba kell mozognia. Tekintsük az alábbi példát, amelyben mindkét koordináták negatívak.
|
Example |
||
|
Problem |
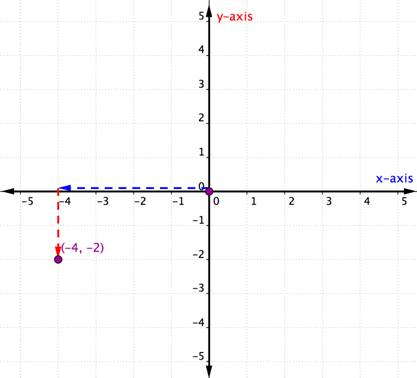
Plot the point (−4, −2). |
|
|
|
||
|
The x-coordinate is −4 because it comes first in the ordered pair. Indítsa el az Origót, és mozgassa a 4 egységet negatív irányba (balra) az x tengely mentén. |
az y-koordináta -2, mert a második a rendezett párban. Most mozgasson 2 egységet negatív irányba (lefelé). Ha az y tengelyre néz, akkor a tengelyen -2-vel kell felsorakoznia. |
|
|
válasz |
rajzoljon egy pontot ezen a helyen, és jelölje meg a pontot (-4, -2). |
|
a pont ábrázolásának lépéseit az alábbiakban foglaljuk össze.
lépések rendezett pár (x, y) ábrázolásához a Koordinátasíkban
O határozza meg az x-koordinátát. Az eredettől kezdve vízszintesen mozogjon, az x tengely irányát, az x-koordináta által megadott távolságot. Ha az x-koordináta pozitív, lépjen jobbra; ha az x-koordináta negatív, LÉPJEN balra.
O határozza meg az y-koordinátát. Az x-koordinátától kezdve függőlegesen mozogjon, az y tengely irányát, az y-koordináta által megadott távolságot. Ha az y-koordináta pozitív, lépjen fel; ha az y-koordináta negatív, lépjen le.
O rajzoljon egy pontot a végponton. Jelölje meg a pontot a megrendelt párral.
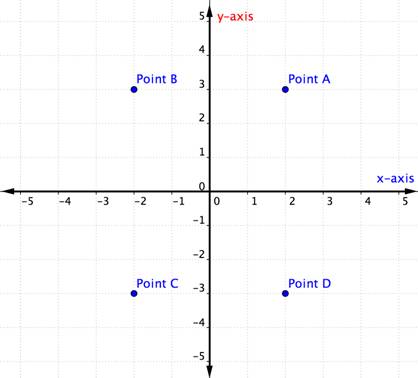
melyik pont képviseli a rendezett párt (-2, -3)?
a négy kvadráns
a rendezett Párok bármely adott kvadránson belül megosztanak bizonyos jellemzőket. Nézze meg az alábbi grafikon minden egyes kvadránsát. Mit vesz észre az egyes kvadránsokban lévő pontok x – és y-koordinátáinak jeleiről?
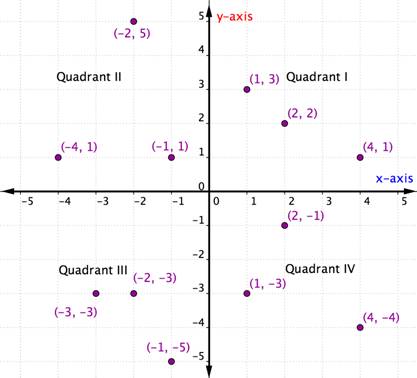
minden kvadránson belül az egyes rendezett Párok x-koordinátáinak és y-koordinátáinak jelei azonosak. Ezek egy mintát is követnek, amelyet az alábbi táblázat vázol fel.
miután megismerte a koordinátasíkban lévő kvadránsokat, meghatározhatja a rendezett pár kvadránsát anélkül, hogy a fenti ábrát megnézné. Itt van egy másik módja annak, hogy gondolkodjunk rajta.
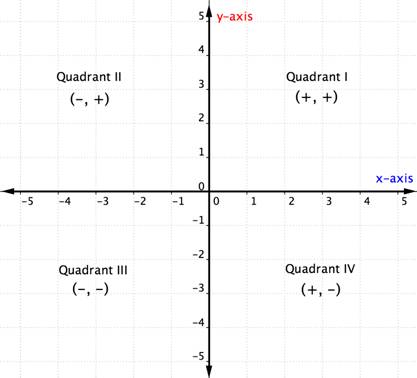
az alábbi példa részletezi, hogyan lehet meghatározni egy pont kvadráns helyét csak a koordináták jeleire gondolva. A kvadráns helyének gondolkodása egy pont megtervezése előtt segíthet megelőzni a hibát. Hasznos ismeretek annak ellenőrzésére is, hogy helyesen ábrázolt-e egy pontot.
mi történik, ha egy rendezett pár X – vagy y-koordinátája nulla? Az alábbi példa a rendezett pár grafikonját mutatja (0, 4).
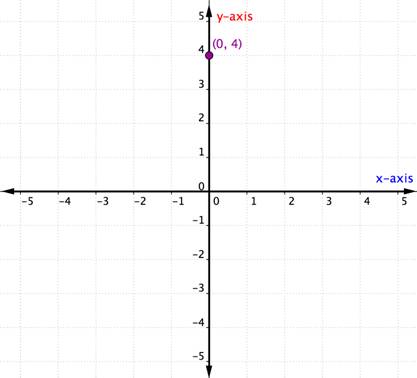
az egyik tengelyen található pont nem tekinthető kvadránsnak. Ez egyszerűen az egyik tengelyen van. Amikor az x-koordináta 0, a pont az y tengelyen található. Hasonlóképpen, minden olyan pont, amelynek y-koordinátája 0, az x tengelyen helyezkedik el.
az alábbi leírások közül melyik írja le legjobban a pont helyét (8, 0)?
A) Kvadráns én
B) az x-tengely
C) az y-tengely
D) A koordináta
Összefoglalás
A koordináta-rendszer grafikus vagy leíró pontok vagy vonalak. A koordináta sík vízszintes (x-) tengelyből és függőleges (y-) tengelyből áll. Ezeknek a vonalaknak a metszéspontja létrehozza az eredetet, amely a pont (0, 0). A koordináta sík négy negyedre oszlik. A koordináta-rendszer ezen funkciói együttesen lehetővé teszik a pontok, vonalak és egyéb algebrai fogalmak grafikus ábrázolását és kommunikációját.