Konigsberg egy város a Preger folyón, amely a 18. században német város volt, de ma már orosz. A városon belül tworiver-szigetek vannak, amelyek hét híddal vannak összekötve a bankokkal (az alábbiak szerint).

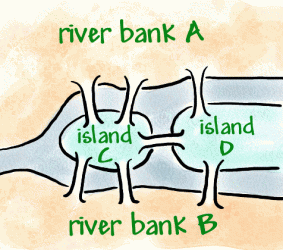
hagyomány lett, hogy megpróbáljunk sétálni a városban oly módon, hogycsak egyszer keresztezték az egyes hídokat, de nehéznek bizonyultproblem. Leonhard Euler, svájci matematikus a szolgálatbannagy Katalin orosz császárné hallott a problémáról.1736-ban Euler bebizonyította, hogy a séta nem lehetséges. Ezt úgy valósította meg, hogy egy hálózatnak nevezett diagramot talált ki, amely csúcsokból (pontokból áll, ahol a vonalak találkoznak) és ívekből(vonalak) áll.

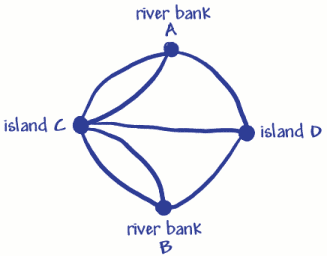
négy pontot (csúcsokat) használt a két folyópartra és a twoislandsre. Ezeket A, B és C, D jelzéssel látták el. a hét vonal (ív) a hét híd. Láthatjuk, hogy 3 híd (ív)csatlakozik az a folyóparthoz, 3 pedig csatlakozik a B. folyóparthoz. 5 hidak (ívek)csatlakoznak a C szigethez, 3 pedig csatlakozik a D szigethez. Ez azt jelenti, hogy mindena csúcsok páratlan számú ívvel rendelkeznek, ezért oddvertices-nek nevezik őket. (Egy egyenletes csúcsnak páros számú arcsjoiningnek kell lennie).
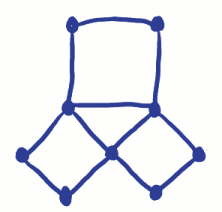
ne feledje, hogy a probléma az volt, hogy az egyes hidakon áthaladó város körül csak egyszer utazzon. Euler hálózatán ez azt jelentette, hogy mindegyiken nyomon követhetőcsak egyszer, az összes csúcs meglátogatásával. Euler bebizonyította, hogy ezt nem lehet megtenni, mert rájött, hogy egy furcsa csúcshoz meg kell kezdeni vagy befejezni az utazást azon a csúcson. (Gondolj bele).Mivel csak egy kezdet és egy vég lehet, csak akkor lehet két páratlan csúcs, ha mindegyiken csak egyszer lehet nyomon követni. Mivel a híd problémájának 4 páratlan csúcsa van, egyszerűen nem lehetséges! Mi történik, ha nincsenek páratlan csúcsok? Nyomon követhető ez a hálózat?

A topológiát számos módon használják, beleértve a tervezéstés a vasúti hálózatok feltérképezését. (Ahhh! A vonatoknak be kellett jönniük….)