más szakaszokban megemlítették, hogy a szilárd anyagok, folyadékok és gázok számos tulajdonsága elszámolható, ha feltételezzük, hogy az anyagok állandóan mozgásban lévő atomokból vagy molekulákból készülnek. Boyle törvénye és a többi gáztörvény sokkal több kvantitatív információt adott nekünk a gázokról, és érdemes megkérdezni, hogy az előző modellel tudunk-e mennyiségi előrejelzéseket készíteni ezekkel a törvényekkel egyetértésben. A kérdés megválaszolásakor fontos betekintést nyerünk a hőmérséklet és a hőenergia természetébe is.

a molekuláris mozgáson alapuló gáz viselkedés mikroszkopikus elméletét a gázok kinetikus elméletének nevezik. Alapvető posztulátumai az 1.táblázatban vannak felsorolva:

táblázat \(\PageIndex{1}\) a gázok kinetikai elméletének posztulátumai.

1 a gázban lévő molekulák kicsiek és nagyon távol vannak egymástól. A gáz által elfoglalt térfogat nagy része üres hely.

2 gázmolekulák állandó véletlenszerű mozgásban vannak. Ugyanolyan sok molekula mozog egy irányban, mint bármely más.

3 molekula ütközhet egymással és a tartály falával. A falakkal való ütközés a gáz nyomását jelenti.

4 ütközések esetén a molekulák nem veszítenek kinetikus energiát; vagyis az ütközések tökéletesen rugalmasak. Az összes molekula teljes kinetikus energiája állandó marad, kivéve, ha külső interferencia van a

5 a molekulák nem gyakorolnak vonzó vagy visszataszító erőket egymásra, kivéve az ütközés folyamatát. Az ütközések között egyenes vonalakban mozognak.

ezekből a gáz nyomására a következő kifejezést lehet levezetni molekuláinak tulajdonságai szempontjából:

\ ahol P, V = A gáz nyomása és térfogata

N = molekulák száma

m = minden molekula tömege

(u2)Ave = az egyes molekuláris sebesség négyzetének átlaga (vagy átlaga). Ezt az átlagos négyzetsebességet azért kell használni, mert a nyomás arányos a molekulasebesség négyzetével, a molekuláris ütközések pedig különböző molekulákat okoznak, amelyek meglehetősen eltérő sebességgel rendelkeznek.

ahelyett, hogy magunkra vonatkoznánk az Eq létrehozásának eljárásával. \(\ref{1}\), vizsgáljuk meg az egyenletet, és nézzük meg, hogy az általános jellemzői mennyi, mint várnánk. Bizonyos szempontból a képlettel való képesség sokkal hasznosabb, mint a levezetés képessége. Ábra \(\PageIndex{1}\)

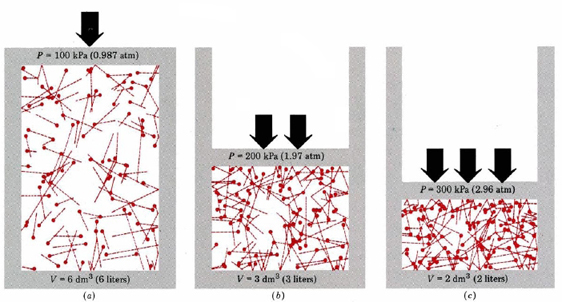először is, az egyenlet azt mondja nekünk, hogy a gáz nyomása arányos a molekulák számával, amelyeket a térfogat oszt meg. Ezt grafikusan ábrázoljuk a \(\PageIndex{1}\) ábrán, ahol egy számítógép ugyanannyi gázmolekulát rajzolt, amelyek mindhárom különböző térfogatot elfoglalják. Az egyes molekulákon a” farok ” megmutatja a pontos utat, amelyet a molekula követ az előző mikroszekundumban—minél hosszabb a farok, annál gyorsabb a molekula. A farokhosszak négyzetének átlaga arányos az (u2)ave-vel, és mindhárom diagramban azonos. Azt is feltételezzük, hogy minden molekulának egyenlő tömege van.

amint láthatja, a gáz térfogatának csökkentése növeli az egységnyi területenkénti ütközések számát a tartály falán. Minden ütközés erőt fejt ki a falon; az egységnyi területre eső erő nyomás, így az egységnyi területre eső ütközések száma arányos a nyomással. A térfogat felére csökkentése megduplázza a nyomást, egy előrejelzést, amely egyetért a Boyle törvényében összefoglalt kísérleti tényekkel. A \(\ref{1}\) egyenlet azt is mondja, hogy a nyomás arányos az egyes gázmolekulák tömegével. Ismét ez az, amit várnánk. A nehéz molekulák nagyobb “lökést”adnak(ennek technikai kifejezése impulzus) a falhoz, mint az azonos sebességgel rendelkező könnyű molekulák.

végül az egyenlet azt mondja nekünk, hogy a nyomás arányos a molekuláris sebesség négyzetének átlagával. Ez a sebesség négyzetétől való függőség ésszerű, ha rájövünk, hogy egy molekula sebességének megduplázása két hatással jár.

először is, a molekula egy adott idő alatt tovább mozoghat, megduplázva a falakkal való ütközések számát. Ez megduplázná a nyomást. Másodszor, a molekula sebességének megduplázása megduplázza az egyes ütközések nyomását vagy impulzusát. Ez ismét megduplázza a nyomást. Ezért a molekula sebességének megduplázása megnégyszerezi a nyomást, és nagyszámú molekula esetében a P arányos az átlagos négyzetsebességgel.