Boyle ‘ s Law
Robert Boyle (1627 – 1691), egy angol kémikus, széles körben tekintik az egyik alapítója a modern kísérleti tudomány kémia. Felfedezte, hogy a zárt gázminta nyomásának megduplázása, miközben a hőmérséklet állandó marad, a gáz térfogata felére csökkent. Boyle törvénye kimondja, hogy egy adott gáztömeg térfogata fordítottan változik a nyomással, amikor a hőmérsékletet állandónak tartják. Az inverz kapcsolatot így írják le. Ahogy az egyik változó növeli az értéket, a másik változó csökken.
fizikailag, mi történik? A gázmolekulák mozognak, és bizonyos távolságra vannak egymástól. A nyomás növekedése közelebb hozza egymáshoz a molekulákat, csökkentve a térfogatot. Ha a nyomás csökken, a gázok szabadon mozoghatnak nagyobb térfogatban.

matematikailag Boyle törvénye az egyenlet segítségével fejezhető ki:
\
A \(k\) egy adott gázminta állandója, és csak a gáz tömegétől és a hőmérséklettől függ. Az alábbi táblázat egy meghatározott mennyiségű gáz állandó hőmérsékleten történő nyomás-és térfogatadatait mutatja. A harmadik oszlop az adatok \(\Bal( k \jobb)\) állandójának értékét jelöli, és mindig megegyezik a térfogattal megszorzott nyomással. Ahogy az egyik változó megváltozik, a másik olyan módon változik, hogy a \(P \times V\) terméke mindig ugyanaz marad. Ebben az esetben ez az állandó \(500 \: \text{atm} \cdot \text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
a táblázatban szereplő adatok grafikonja szemlélteti Boyle törvényének inverz kapcsolat jellegét (lásd az alábbi ábrát). A térfogat a \(x\) tengelyen van ábrázolva, a megfelelő nyomással a \(y\) tengelyen.
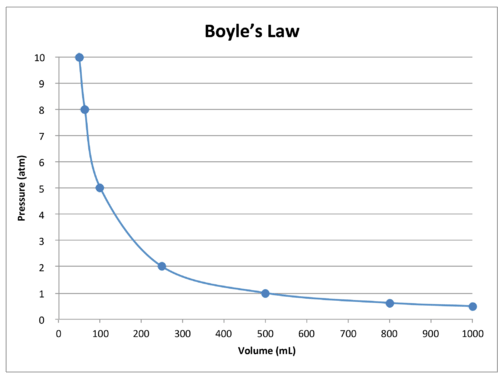
Boyle törvénye a gáz változó feltételeinek összehasonlítására használható. A\ (P_1\) és\ (V_1\) értéket használjuk egy gáz kezdeti nyomására és kezdeti térfogatára. A változás után a\ (P_2\) és\ (V_2\) áll a végső nyomásra és térfogatra. Boyle törvényének matematikai összefüggése a következő lesz:
\
Ez az egyenlet a négy mennyiség bármelyikének kiszámításához használható, ha a másik három ismert.
példa \ (\PageIndex{1}\)
egy oxigéngáz-minta térfogata \(425 \: \ text{mL}\) ha a nyomás egyenlő \(387 \: \text{kPa}\). A gáz a \(1.75 \: \text{L}\) tartályba bővíthető. Számítsa ki a gáz új nyomását.
megoldás
1. lépés: sorolja fel az ismert mennyiségeket, és tervezze meg a problémát.
ismert
- \(P_1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1,75 \: \text{l} = 1750 \: \text{mL}\)
ismeretlen
használja Boyle törvénye megoldani az ismeretlen nyomás \(\bal (P_2 \ jobb)\). Fontos, hogy a két kötet (\(v_1\) és \(V_2\) ugyanabban az egységben legyen kifejezve, tehát \(V_2\) lett konvertálva \(\text{mL}\).
2. lépés: oldja meg.
először rendezze át az egyenletet algebrai módon a \(P_2\) megoldására.
\
most helyettesítse az ismert mennyiségeket az egyenletbe és oldja meg.
\
3.lépés: gondoljon az eredményére.
a térfogat az eredeti értékének valamivel több mint 4-szeresére nőtt, így a nyomás körülbelül egynegyedével csökken. A nyomás \(\text{kPa}\), az értéknek három jelentős alakja van. Vegye figyelembe, hogy bármilyen nyomás vagy térfogategység használható mindaddig, amíg a probléma egészében konzisztensek.