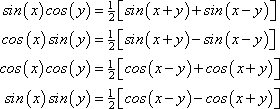Purplemat
matematiikassa ”identiteetti” on yhtälö, joka on aina tosi. Nämä voivat olla” triviaalisesti ”tosia, kuten” x = x ”tai hyödyllisesti tosia, kuten Pythagoraan lauseen” a2 + b2 = c2 ” oikeille kolmioille. On paljon trigonometrisiä identiteettejä, mutta seuraavat ovat niitä, joita todennäköisimmin näette ja käytätte.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Perus-ja Pythagoraan Identiteetit
Affiliate
Huomaa, miten ”co-(jotain)”trig suhde on aina vastavuoroinen joitakin ”ei-co” – suhde. Voit käyttää tätä faktaa auttaa pitämään suorassa, että cosecant menee sini ja secant menee cosine.
seuraavia (erityisesti ensimmäistä kolmesta alla olevasta) kutsutaan ”Pythagoralaisiksi” identiteeteiksi.
sin2(t) + cos2(t) = 1
tan2(t) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
Mainos
huomaa, että ennen kaikkea kolme identiteettiä sisältävät neliöimistä ja luvun 1. Pythagoraan ja Thereomin suhteen voi nähdä selvästi, jos tarkastellaan yksikköympyrää, jossa kulma on t,” vastakkainen ”puoli on sin(t) = y,” viereinen ” puoli on cos(t) = x ja hypotenuusa on 1.
meillä on lisäidentiteettejä, jotka liittyvät trig–suhteiden funktionaaliseen tilaan:
sin (–t) = –sin(t)
cos (–t) = cos(t)
tan (–t) = -tan(t)
huomaa erityisesti, että Sini ja tangentti ovat parittomia funktioita, ovat symmetrisiä Origon suhteen, kun taas kosini on parillinen funktio, ovat symmetrisiä Y-akseli. Se, että voit ottaa argumentin ”miinus” – merkin ulkopuolelle (Sinille ja tangentille) tai poistaa sen kokonaan (kosinille), voi olla hyödyllistä, kun työskentelet monimutkaisten lausekkeiden kanssa.
Kulmasumman ja-eron identiteetit
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α-β) = sin(α – β) cos(β) – cos(α) sin(β)
cos(α – β) = cos(α) cos(β) – sin(α) sin(β)
cos(α-β) = cos(α) cos(β) + sin(α) sin(β)
muuten edellä mainituissa identiteeteissä kulmat merkitään kreikkalaisilla kirjaimilla. A-tyypin kirjainta ”α” kutsutaan ”alfaksi”, joka äännetään ”AL-fuh”. B-tyypin kirjainta, ”β”, kutsutaan ”beetaksi”, joka lausutaan ”BAY-tuh”.
sisältö jatkuu alla
Kaksoiskulma-identiteetit
sin(2x) = 2 sin(x) cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Puolikulma-identiteetit
div>
edellä mainitut identiteetit voidaan ilmoittaa uudelleen neliöimällä kumpikin sivu ja kaksinkertaistamalla kaikki kulmamittaukset. Tulokset ovat seuraavat:
Affiliate

Sum Identities
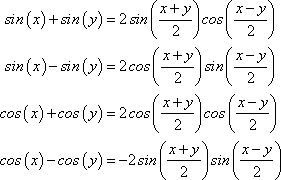
Product Identities
Affiliate
käytät kaikkia näitä identiteettejä, tai lähes niin, muiden trig-identiteettien todistamiseen ja TRIG-yhtälöiden ratkaisemiseen. Kuitenkin, jos aiot opiskella calculus, kiinnitä erityistä huomiota uudelleen sini ja kosini puoli-kulma identiteetit, koska käytät niitä paljon integraalilaskenta.
URL: https://www.purplemath.com/modules/idents.htm