Koordinaattitaso
Oppimistavoite(s)
· piirtää järjestettyjä pareja koordinaattitasolle.
· jos annetaan järjestetty pari, määritetään sen kvadrantti.
Introduction
koordinaatiston kehitti vuosisatoja sitten ranskalainen matemaatikko René Descartes. Hänen kunniakseen järjestelmää kutsutaan joskus Karteesiseksi koordinaatistoksi. Koordinaattitasolla voidaan piirtää pisteitä ja kuvaajalinjoja. Tämä järjestelmä antaa meille mahdollisuuden kuvata algebrallisia suhteita visuaalisessa mielessä ja auttaa meitä myös luomaan ja tulkitsemaan algebrallisia käsitteitä.
tutustuminen koordinaattitasoon
olet todennäköisesti käyttänyt koordinaattitasoa aiemminkin. Oletko esimerkiksi koskaan käyttänyt ruudullista peittokuvaa kohteen sijainnin kartoittamiseen? (Tämäkin tehdään usein tiekarttojen avulla.)

Tämä ”kartta” välittää tietoa kohteen sijainnista vaaka-ja pystysuuntaisella ruudukolla. Huomaa, että kirjaimet A-F on lueteltu yläreunassa ja numerot 1-6 on lueteltu vasemmassa reunassa. Minkä tahansa kohteen yleinen sijainti tässä kartassa löytyy sen ruudukkoruudun kirjaimen ja numeron avulla. Esimerkiksi, voit löytää kohteen, joka on olemassa neliön ” 4F ” siirtämällä sormella pitkin vaakasuorassa kirjaimeen F ja sitten suoraan alas niin olet linjassa 4. Löydät sininen levy on tässä paikassa kartalla.
koordinaatistossa on samanlaisia alkioita kuin yllä esitetyssä ruudukossa. Se koostuu vaaka-ja pystyakselista, lukujonoista, jotka leikkaavat toisensa suorassa kulmassa. (Ne ovat kohtisuorassa toisiinsa nähden.)
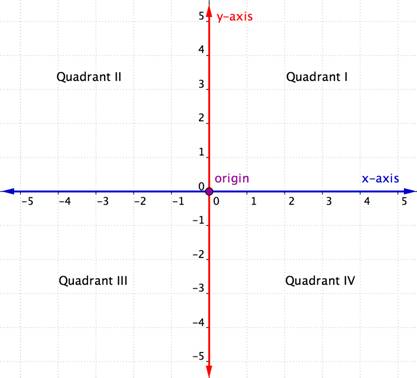
koordinaatiston vaaka-akselia kutsutaan x-akseliksi. Pystyakselia kutsutaan y-akseliksi. Pistettä, jossa kaksi akselia leikkaavat, kutsutaan origoksi. Alkuperä on 0 x-akselilla ja 0 y-akselilla.
leikkaavat x – ja y-akselit jakavat koordinaatiston neljään osaan. Näitä neljää osaa kutsutaan kvadranteiksi. Kvadrantit nimetään roomalaisin numeroin I, II, III ja IV alkaen oikeasta yläkvadrantista ja liikkuen vastapäivään.
koordinaatiston sijainnit kuvataan järjestetyiksi pareiksi. Tilattu pari kertoo pisteen sijainnin suhteuttamalla pisteen sijainnin X-akselilla (tilatun parin ensimmäinen arvo) ja Y-akselilla (tilatun parin toinen arvo).
järjestetyssä parissa, kuten (x, y), ensimmäistä arvoa kutsutaan x-koordinaatistoksi ja toista arvoa y-koordinaatistoksi. Huomaa, että x-koordinaatti on lueteltu ennen y-koordinaattia. Koska Origon x-koordinaatti on 0 ja y-koordinaatti 0, sen järjestyspari kirjoitetaan (0, 0).
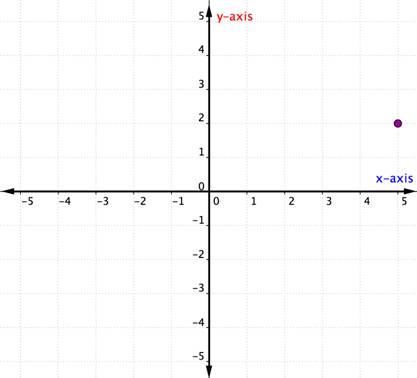
tarkastellaan alla olevaa kohtaa.
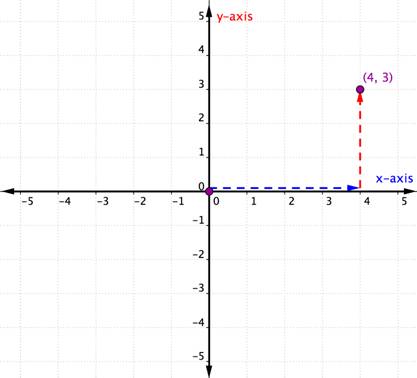
tunnistaaksesi tämän pisteen sijainnin, aloita origosta (0, 0) ja liiku oikealle X-akselia pitkin, kunnes olet pisteen alla. Katso X-akselin etikettiä. 4 osoittaa, että origosta on kulkenut neljä yksikköä oikealle X-akselia pitkin. Tämä on x-koordinaatti, järjestetyn parin ensimmäinen numero.
x-akselilla olevasta 4: stä siirrytään pisteeseen ja huomataan numero, jonka kanssa se asettuu Y-akselilla. 3 osoittaa, että X-akselilta lähdettyäsi matkustit 3 yksikköä ylöspäin pystysuunnassa, Y-akselin suunnassa. Tämä luku on Y-koordinaatti, järjestetyn parin toinen numero. Kun x-koordinaatti on 4 ja y-koordinaatti 3, sinulla on järjestetty pari (4, 3).
katsotaanpa toista esimerkkiä.
|
Example |
||
|
Problem |
Describe the point shown as an ordered pair. |
|
|
|
||
|
(5, y) |
aloita lähtöpaikalta ja liiku X-akselia pitkin. Tämä on x-koordinaatti ja kirjoitetaan ensin järjestetyssä parissa. |
|
|
(5, 2) |
siirrä 5: stä jopa järjestettyyn pariin ja lue numero Y-akselilla. Tämä on y-koordinaatti ja kirjoitetaan järjestyksessä toinen pari. |
|
|
vastaus |
järjestettynä parina esitetty piste on (5, 2). |
|
koordinaatiston pisteiden piirtäminen
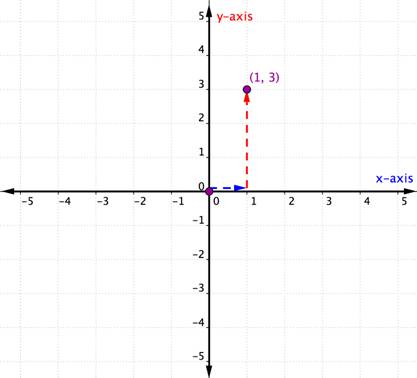
nyt kun osaat käyttää X – ja Y-akseleita, voit piirtää myös järjestetyn parin. Muista vain, että molemmat prosessit alkavat alkuperästä-alusta! Seuraavassa esimerkissä näytetään, miten järjestettyä paria (1, 3) kuvitellaan.
|
Example |
||
|
Problem |
Plot the point (1, 3). |
|
|
|
||
|
The x-coordinate is 1 because it comes first in the ordered pair. Aloita origosta ja siirrä 1 yksikön etäisyys positiiviseen suuntaan (oikealle) origosta X-akselia pitkin. |
y-koordinaatti on 3, koska se tulee järjestetyssä parissa toiseksi. Tästä siirtyä suoraan 3 yksikköä positiiviseen suuntaan (ylös). Jos katsot yli y-akseli, sinun pitäisi olla rivissä kanssa 3 kyseisellä akselilla. |
|
|
vastaus |
Piirrä tähän kohtaan piste ja merkitse piste (1, 3). |
|
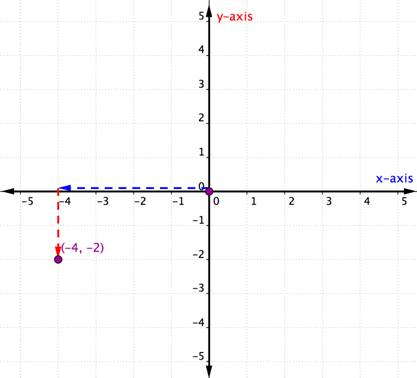
edellisessä esimerkissä sekä x – että y-koordinaatit olivat positiivisia. Kun järjestetyn parin koordinaateista toinen (tai molemmat) on negatiivinen, on siirryttävä negatiiviseen suuntaan yhtä tai molempia akseleita pitkin. Tarkastellaan alla olevaa esimerkkiä, jossa molemmat koordinaatit ovat negatiivisia.
|
Example |
||
|
Problem |
Plot the point (−4, −2). |
|
|
|
||
|
The x-coordinate is −4 because it comes first in the ordered pair. Aloita origosta ja siirrä 4 yksikköä negatiiviseen suuntaan (vasemmalle) X-akselia pitkin. |
y-koordinaatti on -2, koska se tulee järjestetyssä parissa toiseksi. Siirrä nyt 2 yksikköä negatiiviseen suuntaan (alas). Jos katsot y-akselille, sinun pitäisi olla rivissä -2 kyseisellä akselilla. |
|
|
vastaus |
Piirrä tähän kohtaan piste ja merkitse piste (-4, -2). |
|
pisteen merkitsemisen vaiheet on esitetty alla.
vaiheet järjestetyn parin (x, y) piirtämiseksi koordinaatistossa
o määrittävät x-koordinaatin. Alkaen origosta, liikkua vaakasuoraan, suuntaan x-akselin, etäisyys antama x-koordinaatti. Jos x-koordinaatti on positiivinen, siirry oikealle; jos x-koordinaatti on negatiivinen, siirry vasemmalle.
o määrittää y-koordinaatin. X-koordinaatistosta alkaen liikutaan pystysuunnassa, Y-akselin suunta, y-koordinaatiston antama etäisyys. Jos y-koordinaatti on positiivinen, Siirrä ylös; jos y-koordinaatti on negatiivinen, siirry alaspäin.
o piirtää pisteen loppupaikkaan. Merkitse piste tilatulla parilla.
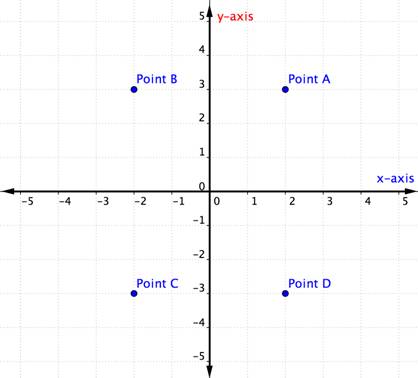
mikä piste edustaa järjestettyä paria (-2, -3)?
neljän kvadrantin
järjestetyt parit minkä tahansa kvadrantin sisällä jakavat tiettyjä ominaisuuksia. Katso jokaista kvadranttia alla olevasta graafista. Mitä huomaatte kunkin kvadrantin pisteiden X – ja y-koordinaattien merkeistä?
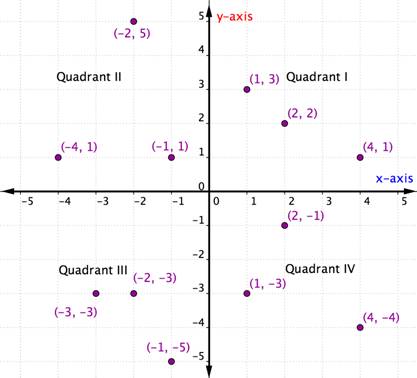
kunkin kvadrantin sisällä kunkin järjestetyn parin x-koordinaattien ja y-koordinaattien merkit ovat samat. Ne noudattavat myös kaavaa, joka on hahmoteltu alla olevassa taulukossa.
kun tietää koordinaattitason kvadranteista, voidaan määrittää järjestetyn parin kvadrantti ilman, että sitä edes kaavoitetaan katsomalla yllä olevaa taulukkoa. Tässä on toinen tapa ajatella sitä.
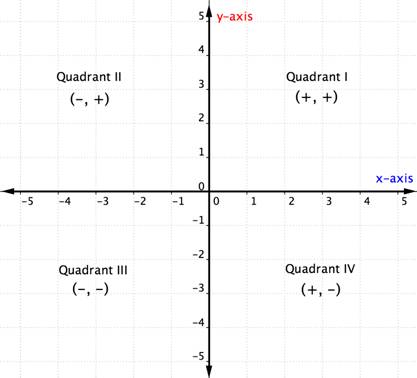
alla olevassa esimerkissä kerrotaan, miten pisteen kvadranttipaikka voidaan määrittää pelkästään sen koordinaattien merkkejä miettimällä. Kvadrantin sijainnin miettiminen ennen pisteen piirtämistä voi auttaa estämään virheen. Se on myös hyödyllistä tietoa tarkistaa, että olet piirtänyt pisteen oikein.
Mitä tapahtuu, jos järjestetyllä parilla on X – tai y-koordinaatti nolla? Alla olevassa esimerkissä esitetään järjestetyn parin (0, 4) kuvaaja.
yhdellä akselilla sijaitsevaa pistettä ei pidetä kvadranttina. Se on vain yhdellä akseleista. Aina kun x-koordinaatti on 0, piste sijaitsee y-akselilla. Vastaavasti mikä tahansa piste, jonka y-koordinaatti on 0, sijaitsee x-akselilla.
mikä alla olevista kuvauksista kuvaa parhaiten pisteen sijaintia (8, 0)?
a) kvadrantti i
b) se on x-akselilla
c) se on y-akselilla
D) koordinaatistossa
Yhteenveto
koordinaatisto on järjestelmä pisteiden ja viivojen kuvaamiseen ja kuvaamiseen. Koordinaatisto koostuu vaaka – (x -) – akselista ja pysty – (y -) – akselista. Näiden janojen leikkauspisteestä syntyy Origo, joka on piste (0, 0). Koordinaatisto jaetaan neljään kvadranttiin. Yhdessä nämä koordinaatiston ominaisuudet mahdollistavat pisteiden, viivojen ja muiden algebrallisten käsitteiden graafisen esittämisen ja kommunikoinnin.