Boylen laki
englantilaista kemistiä Robert Boylea (1627 – 1691) pidetään yleisesti yhtenä modernin kokeellisen kemian tieteen perustajista. Hän havaitsi, että suljetun kaasunäytteen paineen kaksinkertaistaminen samalla kun sen lämpötila pidetään vakiona aiheutti sen, että kaasun tilavuus pieneni puoleen. Boylen lain mukaan tietyn massan kaasun tilavuus vaihtelee kääntäen paineen mukaan, kun lämpötila pidetään vakiona. Käänteistä suhdetta kuvaillaan tällä tavalla. Kun yhden muuttujan arvo kasvaa, toinen muuttuja pienenee.
fyysisesti, mitä tapahtuu? Kaasumolekyylit liikkuvat ja ovat tietyn etäisyyden päässä toisistaan. Paineen nousu työntää molekyylejä lähemmäs toisiaan, jolloin tilavuus pienenee. Jos paine laskee, kaasut pääsevät liikkumaan vapaasti suuremmassa tilavuudessa.

matemaattisesti Boylen laki voidaan ilmaista yhtälöllä:
\
\(k\) on tietyn kaasunäytteen vakio ja riippuu vain kaasun massasta ja lämpötilasta. Alla olevassa taulukossa esitetään paine-ja tilavuustiedot määrätystä kaasumäärästä vakiolämpötilassa. Kolmas sarake kuvaa vakion \(\left( k \right)\) arvoa tälle datalle ja on aina yhtä suuri kuin paine kerrottuna tilavuudella. Kun yksi muuttujista muuttuu, Toinen muuttuu siten, että \(P \times V\): n tulo pysyy aina samana. Tässä tapauksessa kyseinen vakio on \(500 \: \text{atm} \cdot \ text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
kuvaaja taulukon tiedoista edelleen havainnollistaa Boylen lain käänteistä suhdeluontetta (KS.kuva alla). Tilavuus piirretään \(x\) – akselille ja vastaava paine \(y\) – akselille.
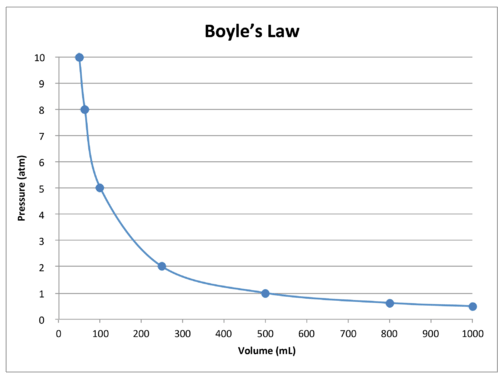
Boylen lakia voidaan käyttää kaasun muuttuvien olosuhteiden vertailuun. Käytämme \(P_1\) ja \(V_1\) edustamaan kaasun alkupainetta ja alkutilavuutta. Kun muutos on tehty, \(P_2\) ja \(V_2\) muodostavat lopullisen paineen ja tilavuuden. Boylen lain matemaattisesta suhteesta tulee:
\
tätä yhtälöä voidaan käyttää minkä tahansa neljästä suureesta laskemiseen, jos muut kolme tunnetaan.
esimerkki \(\PageIndex{1}\)
happikaasun näytteen tilavuus on \(425 \: \text{mL}\), kun paine on \(387 \: \text{kPa}\). Kaasun annetaan laajentua \(1.75\: \text{L}\) säiliöksi. Laske kaasun Uusi paine.
ratkaisu
Vaihe 1: luetteloi tunnetut suureet ja suunnittele ongelma.
tunnettu
- \(P_1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1.75 \: \text{l} = 1750 \: \text{mL}\)
tuntematon
- \(p_2 = ? \ : \text{kPa}\)
käytä Boylen lakia ratkaistaksesi tuntemattoman paineen \(\left( p_2 \right)\). On tärkeää, että kaksi nidettä (\(V_1\) ja \(v_2\)) ilmaistaan samoina yksikköinä, joten \(V_2\) on muunnettu muotoon \(\text{mL}\).
Vaihe 2: ratkaise.
Järjestä ensin yhtälö algebrallisesti ratkaistavaksi \(P_2\).
\
korvaa nyt tunnetut suureet yhtälöön ja ratkaise.
\
Vaihe 3: mieti tulos.
tilavuus on kasvanut hieman yli 4-kertaiseksi alkuperäiseen arvoonsa nähden, joten paine on laskenut noin neljäsosalla. Paine on \(\text{kPa}\) ja arvolla on kolme merkitsevää lukua. Huomaa, että mitä tahansa paine-tai tilavuusyksiköitä voidaan käyttää, kunhan ne ovat yhdenmukaisia koko ongelman ajan.