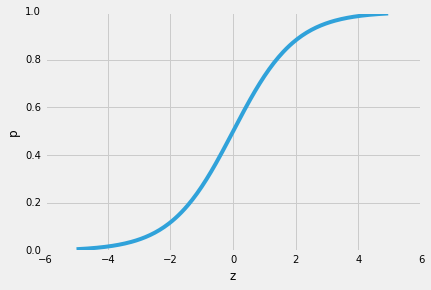
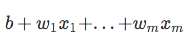Entonces, una de las buenas propiedades de la regresión logística es que la función sigmoide genera las probabilidades condicionales de la predicción, las probabilidades de clase. ¿Cómo funciona?Comencemos con el llamado «odds ratio» p / (1-p), que describe la relación entre la probabilidad de que ocurra un determinado evento positivo y la probabilidad de que no ocurra, donde positivo se refiere al «evento que queremos predecir», es decir, p(y=1 | x).
(Tenga en cuenta que la regresión logística es un tipo especial de función sigmoide, la sigmoide logística; existen otras funciones sigmoides, por ejemplo, la tangente hiperbólica).
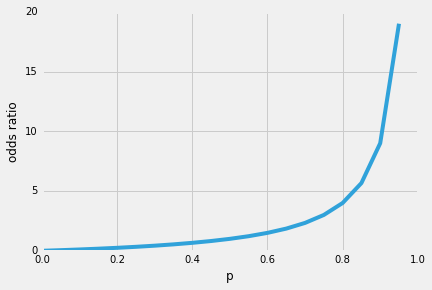
Por lo tanto, cuanto más probable sea que se produzca el evento positivo, mayor será la relación de probabilidades.Ahora, si tomamos el logaritmo natural de esta relación de probabilidades, la función log-odds o logit, obtenemos lo siguiente
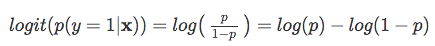
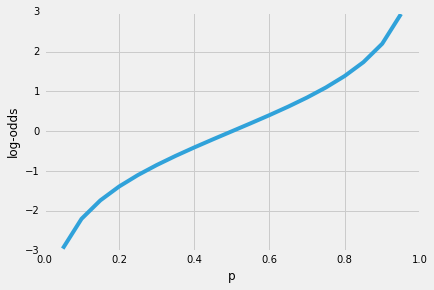
A continuación, usemos esta transformación de registro para modelar la relación entre nuestras variables explicativas y la variable objetivo:
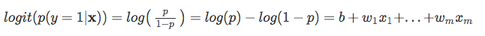
| Ahora, tenga en cuenta que no estamos tratando de predecir la parte correcta de la ecuación anterior, ya que *p(y=1 | x)* es lo que realmente nos interesa. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
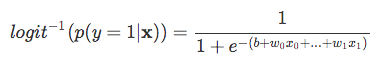
| which returns the class probabilities *p(y=1 | x)* from the inputs |