Purplemath
En matemáticas, una «identidad» es una ecuación que siempre es verdadera. Estos pueden ser» trivialmente «verdaderos, como» x = x «o útilmente verdaderos, como el teorema de Pitágoras» a2 + b2 = c2 » para triángulos rectangulares. Hay un montón de identidades trigonométricas, pero los siguientes son los más propensos a ver y utilizar.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Básico y de Pitágoras Identidades
Afiliados
Observe cómo un «co-(algo)»trig relación siempre es el recíproco de algunos «no-co» de relación. Puede utilizar este hecho para ayudarle a mantener recto que cosecante va con seno y secante va con coseno.
Las siguientes (particularmente la primera de las tres siguientes) se denominan identidades «pitagóricas».
sin2(t) + cos2(t) = 1
tan2(t) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
Anuncio
tenga en cuenta que las tres identidades, sobre todo involucrar a cuadrar y el número 1. Puedes ver la relación Pitagórica-Real claramente si consideras el círculo unitario, donde el ángulo es t, el lado » opuesto «es sin(t) = y, el lado» adyacente » es cos(t) = x, y la hipotenusa es 1.
Tenemos identidades adicionales relacionadas con el estado funcional de las relaciones trigonométricas:
sin(–t) = –sin(t)
cos(–t) = cos(t)
tan(–t) = –tan(t)
Observe en particular que el seno y la tangente son funciones impares, siendo simétricas sobre el origen, mientras que el coseno es una función par, siendo simétrica sobre el eje y. El hecho de que pueda tomar el signo «menos» del argumento fuera (para seno y tangente) o eliminarlo por completo (para coseno) puede ser útil cuando se trabaja con expresiones complicadas.
Ángulo de Suma y de Diferencia de Identidades
sen(α + β) = sen(α) cos(β) + cos(α) sen(β)
sen(α – β) = sen(α) cos(β) – cos(α) sen(β)
cos(α + β) = cos(α) cos(β) – sen(α) sen(β)
cos(α – β) = cos(α) cos(β) + sen(α) sen(β)
Por cierto, en el anterior identidades, los ángulos son denotados por las letras griegas. La letra de tipo a, «α», se llama» alfa», que se pronuncia»AL-fuh». La letra de tipo b, «β», se llama» beta», que se pronuncia»BAY-tuh».
Contenido Sigue a Continuación
Ángulo Doble Identidades
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
la Mitad de Ángulo Identidades
por encima de las identidades pueden ser re-declaró elevando al cuadrado cada lado y doblando todas las medidas de los ángulos. Los resultados son los siguientes:
Affiliate

Sum Identities
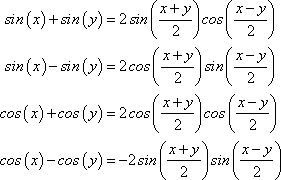
Product Identities
Afiliados
Usted va a utilizar todas estas identidades, o casi, para probar la existencia de otras identidades trigonométricas y resolver ecuaciones trigonométricas. Sin embargo, si vas a estudiar cálculo, presta especial atención a las identidades de medio ángulo seno y coseno reformuladas, porque las usarás mucho en cálculo integral.URL
: https://www.purplemath.com/modules/idents.htm