- Objetivos de aprendizaje
- El trabajo realizado contra la Gravedad
- La conversión entre Energía Potencial y Energía Cinética
- Usando Energía Potencial para Simplificar los Cálculos
- Ejemplo 1. La Fuerza para Dejar de Caer
- Estrategia
- Solución
- Discusión
- Ejemplo 2. Encontrar la Velocidad de una Montaña rusa desde su Altura
- Estrategia
- Solución para la Parte 1
- Solución para la Parte 2
- Discusión e Implicaciones
- Hacer conexiones: Investigación para llevar a casa: Convertir Potencial en Energía Cinética
- Resumen de la sección
- Preguntas conceptuales
- Problemas& Ejercicios
- Glosario
- Soluciones seleccionadas a problemas & Ejercicios
Objetivos de aprendizaje
Al final de esta sección, podrá:
- Explicar la energía potencial gravitacional en términos de trabajo realizado contra la gravedad.
- Muestran que la energía potencial gravitacional de un objeto de masa m a la altura h en la Tierra está dada por PEg = mgh.
- Mostrar cómo se puede utilizar el conocimiento de la energía potencial en función de la posición para simplificar los cálculos y explicar los fenómenos físicos.
El trabajo realizado contra la Gravedad
Subir escaleras y levantar objetos es un trabajo tanto en el sentido científico como en el cotidiano, es un trabajo realizado contra la fuerza gravitacional. Cuando hay trabajo, hay una transformación de la energía. El trabajo realizado contra la fuerza gravitacional entra en una forma importante de energía almacenada que exploraremos en esta sección.

Figura 1. a) El trabajo realizado para levantar el peso se almacena en el sistema masa-Tierra como energía potencial gravitacional. (b) A medida que el peso se mueve hacia abajo, esta energía potencial gravitacional se transfiere al reloj de cuco.
Calculemos el trabajo realizado al levantar un objeto de masa m a través de una altura h, como en la Figura 1. Si el objeto se levanta recto a velocidad constante, entonces la fuerza necesaria para levantarlo es igual a su peso mg. El trabajo realizado en la masa es entonces W = Fd = mgh. Definimos esto como la energía potencial gravitacional (PEg) puesta en (o ganada por) el sistema objeto-Tierra. Esta energía está asociada con el estado de separación entre dos objetos que se atraen entre sí por la fuerza gravitacional. Por conveniencia, nos referimos a esto como la clavija ganada por el objeto, reconociendo que esta es energía almacenada en el campo gravitacional de la Tierra. ¿Por qué usamos la palabra «sistema»? La energía potencial es una propiedad de un sistema en lugar de un solo objeto, debido a su posición física. El potencial gravitacional de un objeto se debe a su posición en relación con el entorno dentro del sistema de objetos de la Tierra. La fuerza aplicada al objeto es una fuerza externa, de fuera del sistema. Cuando hace un trabajo positivo, aumenta la energía potencial gravitacional del sistema. Debido a que la energía potencial gravitacional depende de la posición relativa, necesitamos un nivel de referencia en el que establecer la energía potencial igual a 0. Por lo general, elegimos este punto como la superficie de la Tierra, pero este punto es arbitrario; lo que es importante es la diferencia en la energía potencial gravitacional, porque esta diferencia es lo que se relaciona con el trabajo realizado. La diferencia en la energía potencial gravitacional de un objeto (en el sistema de objetos Terrestres) entre dos peldaños de una escalera será la misma para los dos primeros peldaños que para los dos últimos peldaños.
La conversión entre Energía Potencial y Energía Cinética
La energía potencial gravitacional puede convertirse en otras formas de energía, como la energía cinética. Si liberamos la masa, la fuerza gravitacional hará una cantidad de trabajo igual a mgh en ella, aumentando así su energía cinética en esa misma cantidad (por el teorema de energía de trabajo). Nos resultará más útil considerar solo la conversión de PEg a KE sin considerar explícitamente el paso intermedio del trabajo. (Véase el Ejemplo 2.) Este atajo hace que sea más fácil resolver problemas usando energía (si es posible) en lugar de usar fuerzas explícitamente.
Más precisamente, definimos el cambio en la energía potencial gravitacional ΔPEg como ΔPEg = mgh, donde, para simplificar, denotamos el cambio de altura por h en lugar de la Δh habitual. Tenga en cuenta que h es positiva cuando la altura final es mayor que la altura inicial, y viceversa. Por ejemplo, si una masa de 0,500 kg colgada de un reloj de cuco se eleva 1.00 m, entonces el cambio en la energía potencial gravitacional es
\begin{array}{lll}mgh&&(0.500\text{ kg})(9.80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\text{/s}^2=4.90\text{ J}\end{array}\\
tenga en cuenta que las unidades de la energía potencial gravitatoria de llegar a ser de julios, el mismo que para el trabajo y otras formas de energía. A medida que el reloj avanza, la masa se reduce. Podemos pensar en la masa como renunciar gradualmente a su 4.90 J de energía potencial gravitacional, sin considerar directamente la fuerza de gravedad que hace el trabajo.
Usando Energía Potencial para Simplificar los Cálculos

Figura 2. El cambio en la energía potencial gravitacional (ΔPEg) entre los puntos A y B es independiente de la trayectoria.
La ecuación ΔPEg = mgh se aplica a cualquier trayectoria que tenga un cambio de altura de h, no solo cuando la masa se eleva hacia arriba. (Véase la Figura 2.) Es mucho más fácil calcular mgh (una multiplicación simple) que calcular el trabajo realizado a lo largo de un camino complicado. La idea de energía potencial gravitacional tiene la doble ventaja de que es muy ampliamente aplicable y facilita los cálculos.
A partir de ahora, consideraremos que cualquier cambio en la posición vertical h de una masa m va acompañado de un cambio en la energía potencial gravitacional mgh, y evitaremos la tarea equivalente pero más difícil de calcular el trabajo realizado por o contra la fuerza gravitacional.
ΔPEg = mgh para cualquier camino entre los dos puntos. La gravedad es una de una pequeña clase de fuerzas donde el trabajo realizado por o contra la fuerza depende solo de los puntos de inicio y final, no del camino entre ellos.
Ejemplo 1. La Fuerza para Dejar de Caer
A 60.una persona de 0 kg salta al suelo desde una altura de 3,00 m. Si aterriza rígidamente (con las articulaciones de la rodilla comprimidas en 0,500 cm), calcule la fuerza sobre las articulaciones de la rodilla.
Estrategia
La energía de esta persona se reduce a cero en esta situación por el trabajo realizado en él por el piso mientras se detiene. La clavija inicial se transforma en KE a medida que cae. El trabajo realizado por el suelo reduce esta energía cinética a cero.
Solución
El trabajo realizado en la persona por el piso mientras se detiene está dado por W = Fd cos θ = – Fd, con un signo menos porque el desplazamiento mientras se detiene y la fuerza desde el piso están en direcciones opuestas (cos θ = cos 180º = -1). El suelo elimina la energía del sistema, por lo que hace un trabajo negativo.
La energía cinética que la persona tiene al llegar al suelo es la cantidad de energía potencial perdida al caer a través de la altura h: KE = – ΔPEg = – mgh.
La distancia d a la que se doblan las rodillas de la persona es mucho menor que la altura h de la caída, por lo que se ignora el cambio adicional en la energía potencial gravitacional durante la flexión de la rodilla.
El trabajo W realizado por el piso en la persona detiene a la persona y lleva la energía cinética de la persona a cero: W = – KE = mgh.
La combinación de esta ecuación con la expresión para W da −Fd = mgh.
Recordando que h es negativo porque la persona se cayó, la fuerza sobre las articulaciones de la rodilla viene dada por
\displaystyle{F} = -\frac{mgh} {d}= – \frac {\left(60.0\text{ kg}\right)\left(9.80\text{ m/s}^2\right)\left(-3.00\text{ m}\right)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ N}\\
Discusión
Una fuerza tan grande (500 veces más que el peso de la persona) durante el corto tiempo de impacto es suficiente para romper huesos. Una forma mucho mejor de amortiguar el impacto es doblando las piernas o rodando en el suelo, aumentando el tiempo durante el cual actúa la fuerza. Un movimiento de flexión de 0,5 m de esta manera produce una fuerza 100 veces menor que en el ejemplo. Un salto de canguro muestra este método en acción. El canguro es el único animal grande que usa el salto para la locomoción, pero el choque en el salto es amortiguado por la flexión de sus patas traseras en cada salto. (Véase la Figura 3.)

Figura 3. El trabajo realizado por el suelo sobre el canguro reduce su energía cinética a cero a medida que aterriza. Sin embargo, al aplicar la fuerza del suelo sobre las patas traseras a una distancia más larga, el impacto en los huesos se reduce. (crédito: Chris Samuel, Flickr)
Ejemplo 2. Encontrar la Velocidad de una Montaña rusa desde su Altura
- ¿Cuál es la velocidad final de la montaña rusa que se muestra en la Figura 4 si comienza desde el descanso en la cima de la colina de 20,0 m y el trabajo realizado por fuerzas de fricción es insignificante?
- ¿Cuál es su velocidad final (suponiendo de nuevo una fricción insignificante) si su velocidad inicial es de 5,00 m/s?
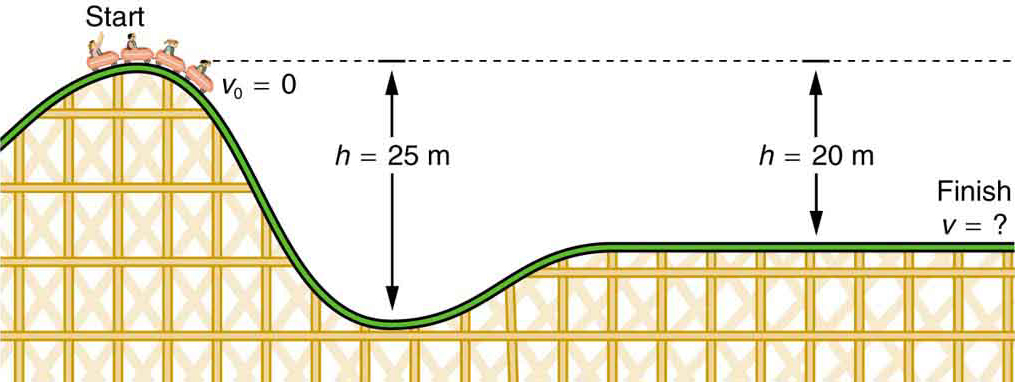
Figura 4. La velocidad de una montaña rusa aumenta a medida que la gravedad la tira cuesta abajo y es mayor en su punto más bajo. Visto en términos de energía, la energía potencial gravitacional del sistema Tierra-montaña rusa se convierte en energía cinética. Si el trabajo realizado por fricción es insignificante, todo ΔPEg se convierte en KE.
Estrategia
La montaña rusa pierde energía potencial a medida que va cuesta abajo. Descuidamos la fricción, de modo que la fuerza restante ejercida por la pista es la fuerza normal, que es perpendicular a la dirección del movimiento y no funciona. El trabajo de red en la montaña rusa se realiza solo por gravedad. La pérdida de energía potencial gravitacional al moverse hacia abajo a través de una distancia h es igual a la ganancia de energía cinética. Esto se puede escribir en forma de ecuación como-ΔPEg = ΔKE. Usando las ecuaciones para PEg y KE, podemos resolver para la velocidad final v, que es la cantidad deseada.
Solución para la Parte 1
Aquí la energía cinética inicial es cero, de modo que \Delta\text{KE}=\frac{1}{2}mv^2\\. La ecuación para el cambio en la energía potencial establece que ΔPEg = mgh. Dado que h es negativo en este caso, reescribiremos esto como ΔPEg = −mg|h| para mostrar claramente el signo menos. Por lo tanto, – ΔPEg = ΔKE se convierte en mg|h|=\frac{1}{2}{mv}^2\\.
Resolviendo para v, encontramos que la masa se cancela y que v=\sqrt{2g|h|}\\.
Sustituyendo los valores conocidos,
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\derecho)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
Solución para la Parte 2
de Nuevo −ΔPEg = ΔKE. En este caso, hay una energía cinética inicial, por lo que
\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
por Lo tanto, mg|h|=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
Reorganizar da \frac{1}{2}mv^2=mg|h|+\frac{1}{2}mv+0^2\\.
Esto significa que la energía cinética final es la suma de la energía cinética inicial y la energía potencial gravitacional. La masa se cancela de nuevo, y v = \sqrt{2g / h / +v_0^2}\\.
Esta ecuación es muy similar a la ecuación cinemática v = \sqrt{v_0^2 + 2ad}\\, pero es más general: la ecuación cinemática es válida solo para la aceleración constante, mientras que nuestra ecuación anterior es válida para cualquier camino independientemente de si el objeto se mueve con una aceleración constante. Ahora, sustituyendo los valores conocidos da
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\derecho)\left(20.0\text{ m}\derecho)+\left(5.00\text{ m/s}\derecho)^2}\\\text{ }&&20.4\text{ m/s}\end{array}\\
Discusión e Implicaciones
En primer lugar, tenga en cuenta que las cancelaciones masivas. Esto es bastante consistente con las observaciones hechas en Objetos que caen de que todos los objetos caen a la misma velocidad si la fricción es insignificante. En segundo lugar, solo se considera la velocidad de la montaña rusa; no hay información sobre su dirección en ningún punto. Esto revela otra verdad general. Cuando la fricción es insignificante, la velocidad de un cuerpo que cae depende solo de su velocidad y altura iniciales, y no de su masa o el camino recorrido. Por ejemplo, la montaña rusa tendrá la misma velocidad final, ya sea que caiga 20,0 m en línea recta o tome un camino más complicado como el de la figura. En tercer lugar, y tal vez inesperadamente, la velocidad final en la parte 2 es mayor que en la parte 1, pero por mucho menos de 5,00 m/s. Finalmente, tenga en cuenta que la velocidad se puede encontrar a cualquier altura en el camino simplemente utilizando el valor apropiado de h en el punto de interés.
Hemos visto que el trabajo realizado por o contra la fuerza gravitacional depende solo de los puntos de inicio y final, y no del camino entre ellos, lo que nos permite definir el concepto simplificador de energía potencial gravitacional. Podemos hacer lo mismo con algunas otras fuerzas, y veremos que esto conduce a una definición formal de la ley de conservación de la energía.
Hacer conexiones: Investigación para llevar a casa: Convertir Potencial en Energía Cinética
En este experimento se puede estudiar la conversión de energía potencial gravitacional en energía cinética. En una superficie lisa y nivelada, use una regla del tipo que tenga una ranura a lo largo de su longitud y un libro para hacer una inclinación (consulte la Figura 5). Coloque una canica en la posición de 10 cm de la regla y déjela rodar por la regla. Cuando llegue a la superficie nivelada, mida el tiempo que tarda en rodar un metro. Ahora coloque la canica en las posiciones de 20 cm y 30 cm y mida de nuevo los tiempos necesarios para rodar 1 m sobre la superficie nivelada. Encuentra la velocidad de la canica en la superficie nivelada para las tres posiciones. Trazar la velocidad al cuadrado versus la distancia recorrida por la canica. ¿Cuál es la forma de cada parcela? Si la forma es una línea recta, la gráfica muestra que la energía cinética de la canica en la parte inferior es proporcional a su energía potencial en el punto de liberación.

Figura 5. Una canica rueda por una regla, y se mide su velocidad en la superficie nivelada.
Resumen de la sección
- El trabajo realizado contra la gravedad al levantar un objeto se convierte en energía potencial del sistema objeto-Tierra.
- El cambio en la energía potencial gravitacional, ΔPEg, es ΔPEg = mgh, siendo h el aumento de altura y g la aceleración debida a la gravedad.
- La energía potencial gravitacional de un objeto cerca de la superficie de la Tierra se debe a su posición en el sistema masa-Tierra. Solo las diferencias en la energía potencial gravitacional, ΔPEg, tienen significación física.
- A medida que un objeto desciende sin fricción, su energía potencial gravitacional cambia a energía cinética correspondiente al aumento de velocidad, de modo que ΔKE = −ΔPEg
Preguntas conceptuales
- En el Ejemplo 2, calculamos la velocidad final de una montaña rusa que descendió 20 m de altura y tuvo una velocidad inicial de 5 m/s cuesta abajo. Supongamos que la montaña rusa hubiera tenido una velocidad inicial de 5 m/s cuesta arriba en su lugar, y avanzara cuesta arriba, se detuviera y luego volviera a rodar hasta un punto final 20 m por debajo de la salida. Encontraríamos en ese caso que tenía la misma velocidad final. Explicar en términos de conservación de energía.
- ¿El trabajo que haces en un libro cuando lo subes a un estante depende del camino que tomes? En el tiempo? ¿A la altura del estante? En la misa del libro?
Problemas& Ejercicios
- Una instalación de energía hidroeléctrica (ver Figura 6) convierte la energía potencial gravitacional del agua detrás de una presa en energía eléctrica. a) Cuál es la energía potencial gravitacional en relación con los generadores de un lago de volumen 50.0 km3 (masa = 5,00 × 1013 kg), dado que el lago tiene una altura media de 40,0 m por encima de los generadores? (b) Compare esto con la energía almacenada en una bomba de fusión de 9 megatones.

Figura 6. Instalación hidroeléctrica (crédito: Denis Belevich, Wikimedia Commons)
- (a) Cuánta energía potencial gravitacional (en relación con el suelo sobre el que está construida) se almacena en la Gran Pirámide de Keops, dado que su masa es de aproximadamente 7 × 109 kg y su centro de masa es de 36.¿5 m por encima del suelo circundante? b) ¿Cómo se compara esta energía con la ingesta diaria de alimentos de una persona?
- Supongamos que un kookaburra de 350 g (un gran martín pescador) recoge una serpiente de 75 g y la eleva 2,5 m desde el suelo hasta una rama. (a) ¿Cuánto trabajo hizo el pájaro en la serpiente? (b) ¿Cuánto trabajo hizo para elevar su propio centro de masa a la rama?
- En el ejemplo 2, encontramos que la velocidad de una montaña rusa que había descendido 20,0 m era solo ligeramente mayor cuando tenía una velocidad inicial de 5,00 m/s que cuando comenzó en reposo. Esto implica que ΔPE >> KEi. Confirme esta afirmación tomando la relación de ΔPE a KEi. (Tenga en cuenta que la masa se cancela.)
- Un coche de juguete de 100 g es propulsado por un resorte comprimido que lo pone en movimiento. El coche sigue la pista curva de la Figura 7. Mostrar que la velocidad final del auto de juguete es 0.687 m/s si su velocidad inicial es de 2.00 m/s y costas hasta la pendiente sin fricción, ganando 0.180 m de altitud.

Figura 7. Un coche de juguete se mueve por una pista inclinada. (crédito: Leszek Leszczynski, Flickr)
- En una carrera de esquí alpino, sorprendentemente, se obtiene poca ventaja al comenzar a correr. (Esto se debe a que la energía cinética inicial es pequeña en comparación con la ganancia de energía potencial gravitacional incluso en colinas pequeñas.) Para demostrarlo, encuentra la velocidad final y el tiempo que tarda un esquiador que vuela 70,0 m a lo largo de una pendiente de 30º sin tener en cuenta la fricción: (a) Comenzar desde el descanso. (b) Comenzando con una velocidad inicial de 2,50 m/s. (c) ¿Le sorprende la respuesta? Discuta por qué sigue siendo ventajoso comenzar a correr en eventos muy competitivos.
Glosario
energía potencial gravitacional: la energía que tiene un objeto debido a su posición en un campo gravitacional
Soluciones seleccionadas a problemas & Ejercicios
1. (a) 1,96 × 1016 J; (b) La relación entre la energía potencial gravitacional en el lago y la energía almacenada en la bomba es de 0,52. Es decir, la energía almacenada en el lago es aproximadamente la mitad de la de una bomba de fusión de 9 megatones.
3. a) 1,8 J; b) 8,6 J
5. {v}_{f} = \sqrt{2gh+{v_0}^2}=\sqrt{2 \ left (9.80 \ text{ m/s}^2 \ right) \ left(-0.180 \ text{ m} \ right)+\left (2.00\text{ m/s}\right)^2} = 0.687 \ text{ m / s}\ \