Después de comprender la función exponencial, nuestro siguiente objetivo es el logaritmo natural.

Dado cómo se describe el logaritmo natural en los libros de matemáticas, hay poco de «natural» en él: se define como el inverso de e e^x$, un exponente bastante extraño ya.

Pero hay una explicación fresca e intuitiva: El logaritmo natural te da el tiempo necesario para alcanzar un cierto nivel de crecimiento.

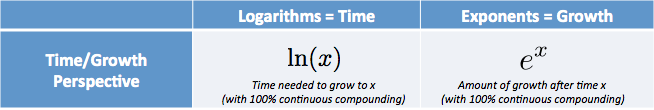
Supongamos que tiene una inversión en osos gomosos (¿quién no?) con una tasa de interés del 100% anual, en continuo crecimiento. Si desea un crecimiento de 10 veces, suponiendo una composición continua, esperaría solo \ \ ln (10) or o 2.302 años. ¿No ves por qué solo se necesitan unos pocos años para obtener un crecimiento de 10 veces? ¿No ves por qué el patrón no es 1, 2, 4, 8? Leer más sobre e.

e y el Logaritmo Natural son gemelos:

• e e^x is es la cantidad que tenemos después de comenzar en 1.0 y en constante crecimiento por $x$ unidades de tiempo
• $\ln(x)$ (Logaritmo Natural) es el tiempo para llegar a la cantidad de $x$, suponiendo que hemos crecido continuamente desde 1.0

No es tan malo, ¿cierto? Mientras los matemáticos se apresuran a darte la explicación larga y técnica, vamos a sumergirnos en la intuitiva.

E es sobre Crecimiento

El número e es sobre crecimiento continuo. Como vimos la última vez, $e^x lets nos permite fusionar la tasa y el tiempo: 3 años con un crecimiento del 100% es lo mismo que 1 año con un crecimiento del 300%, cuando se compone continuamente.

Podemos tomar cualquier combinación de tarifa y tiempo (50% durante 4 años) y convertir la tarifa al 100% para mayor comodidad (nos da el 100% durante 2 años). Al convertir a una tasa del 100%, solo tenemos que pensar en el componente de tiempo:

Intuitivamente, Intu e^x means significa:

• Cuánto crecimiento obtengo después de x unidades de tiempo (y 100% de crecimiento continuo)
• Por ejemplo: después de 3 períodos de tiempo tengo $e^3 = = 20.08 veces la cantidad de «cosas».

$e^x is es un factor de escala, que nos muestra cuánto crecimiento obtendríamos después de units x units unidades de tiempo.

El logaritmo natural es Sobre el tiempo

El logaritmo natural es el inverso de $e^x$, un término sofisticado para lo opuesto. Hablando de fantasía, el nombre latino es logarithmus naturali, dando la abreviatura ln.

Ahora, ¿qué significa esto inverso u opuesto?

• e e^x lets nos permite conectar el tiempo y obtener crecimiento.
• \ \ ln (x) lets nos permite conectar el crecimiento y obtener el tiempo que llevaría.

Por ejemplo:

• $e^3$ es 20.08. Después de 3 unidades de tiempo, terminamos con 20.08 veces con lo que empezamos.
• \ \ ln (20.08) is es aproximadamente 3. Si queremos un crecimiento de 20,08, esperaríamos 3 unidades de tiempo (de nuevo, suponiendo una tasa de crecimiento continuo del 100%).

conmigo? El tronco natural nos da el tiempo necesario para alcanzar nuestro crecimiento deseado.

La aritmética logarítmica No Es Normal

Has estudiado troncos antes, y eran bestias extrañas. ¿Cómo convirtieron la multiplicación en suma? ¿División en resta? Veamos.

¿Qué es $ \ ln(1)?? Intuitivamente, la pregunta es: ¿Cuánto tiempo espero para obtener 1x mi cantidad actual?

Cero. Postal. Nada. ¡Ya estás en 1x tu cantidad actual! No se necesita tiempo para crecer de 1 a 1.

• $\ln(1) = 0$

Ok, ¿qué tal un valor fraccionario? ¿Cuánto tiempo para obtener 1/2 de mi cantidad actual? Suponiendo que está creciendo continuamente al 100%, sabemos que $\ln(2) is es la cantidad de tiempo que se duplica. Si lo invertimos (es decir, tomamos el tiempo negativo) tendríamos la mitad de nuestro valor actual.

• \ \ ln(.5) – – \ln (2)= -.693$

tiene sentido, ¿verdad? Si retrocedemos .693 unidades (segundos negativos, digamos) tendríamos la mitad de nuestra cantidad actual. En general, puede voltear la fracción y tomar el negativo: $\ln(1/3) = – \ln(3) = -1.09$. Esto significa que si retrocedemos 1,09 unidades de tiempo, tendríamos un tercio de lo que tenemos ahora.

Ok, ¿qué tal el logaritmo natural de un número negativo? ¿Cuánto tiempo se tarda en «hacer crecer» su colonia de bacterias de 1 a -3?

Es imposible! No puedes tener una cantidad» negativa » de bacterias, ¿verdad? A lo sumo (er least al menos) puedes tener cero, pero no hay manera de tener una cantidad negativa de los pequeños bichos. Las bacterias negativas no tienen sentido.

• \ \ ln (\text{número negativo}) = \text{indefinido} Und

Indefinido solo significa «no hay cantidad de tiempo que pueda esperar» para obtener una cantidad negativa. (Bueno, si usamos exponenciales imaginarios, hay una solución. Pero hoy seamos realistas.)

La multiplicación logarítmica es muy divertida

¿Cuánto tiempo se tarda en crecer 9 veces su cantidad actual? Claro, podríamos usar ln (9). Pero eso es demasiado fácil, seamos diferentes.

Podemos considerar un crecimiento de 9 veces como triplicar (tomar units\ln(3) units unidades de tiempo) y luego triplicar de nuevo (tomar otro units\ln(3) units unidades de tiempo):

• Tiempo para crecer 9x = \\ln(9) = = Tiempo para triplicar y triplicar de nuevo = \ \ ln(3) + \ ln(3) Interesting

Interesante. Cualquier número de crecimiento, como 20, se puede considerar crecimiento 2 veces seguido de crecimiento 10 veces. O crecimiento de 4 veces seguido de crecimiento de 5 veces. O crecimiento de 3 veces seguido de crecimiento de 6.666 veces. Ver el patrón?

• $\ln(a*b) = \ln(a) + \ln(b)$

El registro de los tiempos de b = log(a) + log(b). Esta relación tiene sentido cuando piensas en términos de tiempo para crecer.

Si queremos crecer 30x, podemos esperar $\ln(30)$ todos a la vez, o simplemente esperar $\ln(3)$, triplicar, a continuación, esperar $\ln(10)$, para crecer 10x de nuevo. El efecto neto es el mismo, por lo que el tiempo neto también debería ser el mismo (y lo es).

¿Qué tal la división? $\ln (5/3) means significa: ¿Cuánto tiempo se tarda en crecer 5 veces y luego tomar 1/3 de eso?

Bien, crecer 5 veces es $\ln (5)$. Crecer 1/3 es units – \ln(3) units unidades de tiempo. Así que

• \\ln(5/3) = \ln(5) – \ ln(3)

Que dice: Crece 5 veces y «retrocede en el tiempo» hasta que tengas un tercio de esa cantidad, por lo que te quedas con un crecimiento de 5/3. En general, tenemos

• $\ln(a/b) = \ln(a) – \ln(b)$

espero que el extraño matemáticas de los logaritmos se empieza a tener sentido: la multiplicación del crecimiento se convierte en adición de tiempo, la división del crecimiento se convierte en resta de tiempo. No memorices las reglas, entiéndelas.

Usando Troncos Naturales Con Cualquier Tasa

«Claro», dices, » Este material de troncos funciona para un crecimiento del 100%, pero ¿qué pasa con el 5% que normalmente obtengo?»

no hay problema. El » tiempo «que obtenemos de $\ln () is es en realidad una combinación de velocidad y tiempo, la» x » de nuestra ecuación e e^x x. Asumimos el 100% para hacerlo simple, pero podemos usar otros números.

Supongamos que queremos un crecimiento de 30 veces: conecte $\ln( 30) get y obtenga 3.4. Esto significa:

• $e^x = \ text{crecimiento}
• e e^{3.4} = 30

E intuitivamente esta ecuación significa que «el rendimiento del 100% durante 3,4 años es un crecimiento de 30 veces». Podemos considerar la ecuación:

se puede modificar el «ritmo» y «el tiempo», mientras la tasa de * tiempo = 3.4. Por ejemplo, supongamos que queremos un crecimiento de 30 veces, ¿cuánto tiempo esperamos suponiendo un retorno del 5%?

• \ \ ln (30) = 3.4
• \\text{rate} * \ text{time} = 3.4
• $.05 * \text{time} = 3.4
• \ \ text{time} = 3.4/.05 = 68 \text{años} Intu

Intuitivamente, creo que » $\ln (30) = 3,4$, por lo que con un crecimiento del 100% tomará 3,4 años. Si doblo la tasa de crecimiento, reduzco a la mitad el tiempo necesario.»

• 100% 3,4 años = 1.0 * 3.4 = 3.4
• 200% 1,7 años = 2.0 * 1.7 = 3.4
• 50% 6,8 años = 0.5 * 6.8 = 3.4
• 5% 68 años = .05 * 68 = 3.4

Genial, ¿eh? El logaritmo natural se puede usar con cualquier tipo de interés o tiempo, siempre y cuando su producto sea el mismo. Puedes mover las variables todo lo que quieras.

Ejemplo impresionante: La Regla de 72

La Regla de 72 es un atajo de matemáticas mentales para estimar el tiempo necesario para duplicar su dinero. Vamos a derivarlo (yay! y aún mejor, vamos a entenderlo intuitivamente.

¿Cuánto tiempo se tarda en duplicar su dinero al 100% de interés, compuesto cada año?

Uh oh. Hemos estado usando logaritmo natural para tasas continuas, ¿pero ahora estás pidiendo intereses anuales? ¿Esto no estropeará nuestra fórmula? Sí, lo hará, pero a tasas de interés razonables como el 5%, el 6% o incluso el 15%, no hay mucha diferencia entre el interés compuesto anual y el completamente continuo. Así que la fórmula en bruto funciona, aproximadamente y fingiremos que estamos recibiendo un interés completamente continuo.

Ahora la pregunta es fácil: ¿Cuánto tiempo se duplica al 100% de interés? ln (2) = .693. Se necesita .693 unidades de tiempo (años, en este caso) para duplicar su dinero con una composición continua con una tasa del 100%.

Ok, ¿qué pasa si nuestro interés no es 100% Y si es 5% o 10%?

Simple. Siempre y cuando rate * time=.693, duplicaremos nuestro dinero:

• tasa * tiempo = .693
• time = .693 / rate

Así que, si solo tuviéramos un crecimiento del 10%, se necesitaría .693 / .10 o 6.93 años para duplicar.

Para simplificar las cosas, multipliquemos por 100 para que podamos hablar de 10 en lugar de.10:

• tiempo hasta el doble = 69,3 / tasa, donde se supone que la tasa está en porcentaje.

Ahora el momento de duplicarse con un crecimiento del 5% es de 69,3/5 o 13,86 años. Sin embargo, 69.3 no es el número más divisible. Vamos a elegir un vecino cercano, 72, que se puede dividir por 2, 3, 4, 6, 8 y muchos más números.

• el tiempo para doble = 72/tasa

que es la regla del 72! Tranquilo, ventoso.

Si desea encontrar el tiempo para triplicar, use ln (3) ~ 109.8 y obtenga

• tiempo para triplicar = 110 / tasa

, que es otra regla práctica útil. La Regla de 72 es útil para las tasas de interés, el crecimiento de la población, los cultivos de bacterias y cualquier cosa que crezca exponencialmente.

¿A dónde ir desde aquí?

Espero que el logaritmo natural tenga más sentido: te indica el tiempo necesario para cualquier cantidad de crecimiento exponencial. Lo considero «natural» porque e es la tasa de crecimiento universal, por lo que ln podría considerarse la forma «universal» de averiguar cuánto tiempo tardan las cosas en crecer.

Cuando vea $\ln (x) think, simplemente piense «la cantidad de tiempo para crecer a x». En el próximo artículo, uniremos e y ln, y el dulce aroma de las matemáticas llenará el aire.

Apéndice: El Logaritmo natural de E

Quick quiz: ¿Qué es $ \ ln (e)??

• El robot matemático dice: Debido a que se definen como funciones inversas, claramente \ \ ln (e) = 1
• El humano intuitivo: ln (e) es la cantidad de tiempo que se tarda en obtener unidades «e» de crecimiento (aproximadamente 2.718). Pero e es la cantidad de crecimiento después de 1 unidad de tiempo, por lo que $\ln (e) = 1$.

Piensa intuitivamente.

Otros Posts De Esta Serie

1. Una Guía Intuitiva De Funciones Exponenciales & e
2. Desmitificar el Logaritmo Natural (ln)
3. Una Guía Visual de Tasas de Interés Simples, Compuestas y Continuas
4. Definiciones Comunes de e (Coloreado)
5. Entender los Exponentes (¿Por qué 0^0 = 1?)
6. Usar Logaritmos en el Mundo Real
7. Cómo Pensar Con Exponentes Y Logaritmos
8. Entender el Crecimiento Discreto vs. Continuo
9. ¿Qué significa realmente un exponente?
10. P: ¿Por qué e es especial? (2.718…, ¿no 2, 3,7 u otro número?)