En otras secciones se mencionó que muchas de las propiedades de sólidos, líquidos y gases podrían explicarse si asumimos que las sustancias están hechas de átomos o moléculas que están en constante movimiento. La ley de Boyle y las otras leyes de gas nos han dado ahora mucha más información cuantitativa sobre los gases, y vale la pena preguntarse si con el modelo anterior podemos hacer predicciones cuantitativas de acuerdo con estas leyes. Al responder a esta pregunta, también obtendremos información importante sobre la naturaleza de la temperatura y de la energía térmica.

La teoría microscópica del comportamiento de los gases basada en el movimiento molecular se denomina teoría cinética de los gases. Sus postulados básicos se enumeran en la Tabla 1:

Postulados de la Teoría Cinética de los Gases de la TABLA \(\pageIndex{1}\).

1 Las moléculas de un gas son pequeñas y muy separadas. La mayor parte del volumen que ocupa un gas es espacio vacío.

2 Moléculas de gas están en movimiento aleatorio constante. Tantas moléculas se mueven en una dirección como en cualquier otra.

3 moléculas pueden chocar entre sí y con las paredes del recipiente. Las colisiones con las paredes explican la presión del gas.

4 Cuando se producen colisiones, las moléculas no pierden energía cinética; es decir, se dice que las colisiones son perfectamente elásticas. La energía cinética total de todas las moléculas permanece constante a menos que haya alguna interferencia externa con el

5 Las moléculas no ejercen fuerzas atractivas o repulsivas entre sí, excepto durante el proceso de colisión. Entre colisiones, se mueven en líneas rectas.

De ellos es posible derivar la siguiente expresión para la presión de un gas en términos de las propiedades de sus moléculas:

\ Donde P, V = presión y volumen del gas

N = número de moléculas

m = masa de cada molécula

(u2)ave = promedio (o media) de los cuadrados de todas las velocidades moleculares individuales. Esta velocidad cuadrada media debe usarse porque la presión es proporcional al cuadrado de la velocidad molecular, y las colisiones moleculares hacen que diferentes moléculas tengan velocidades muy diferentes.

En lugar de preocuparnos por el procedimiento para derivar la Ec. \(\ref{1}\), inspeccionemos la ecuación y veamos que sus características generales son mucho más de lo que esperaríamos. En cierto modo, la capacidad de hacer esto con una fórmula es más útil que la capacidad de derivarla. Figura \(\pageIndex{1}\)

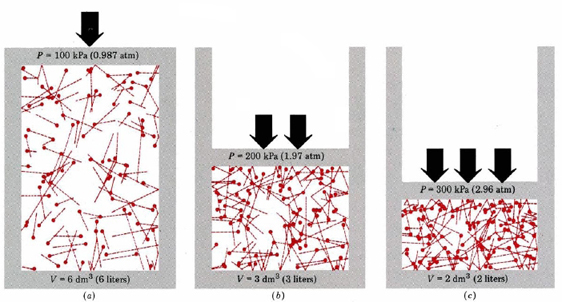En primer lugar, la ecuación nos dice que la presión de un gas es proporcional al número de moléculas dividido por el volumen. Esto se muestra gráficamente en la Figura \(\pageIndex{1}\), donde un ordenador ha dibujado el mismo número de moléculas de gas ocupando cada uno de tres volúmenes diferentes. La «cola» de cada molécula muestra el camino exacto seguido por esa molécula en el microsegundo anterior: cuanto más larga era la cola, más rápido iba la molécula. El promedio de los cuadrados de las longitudes de cola es proporcional a (u2)ave y es el mismo en los tres diagramas. También se asume que todas las moléculas tienen masas iguales.

Como puede ver, reducir el volumen del gas aumenta el número de colisiones por unidad de área en las paredes del contenedor. Cada colisión ejerce fuerza en la pared; la fuerza por unidad de área es presión, por lo que el número de colisiones por unidad de área es proporcional a la presión. Reducir a la mitad el volumen duplica la presión, una predicción que concuerda con los hechos experimentales resumidos en la ley de Boyle. La ecuación \(\ref{1}\) también dice que la presión es proporcional a la masa de cada molécula de gas. Una vez más, esto es lo que esperaríamos. Las moléculas pesadas dan un «empuje»más grande(el término técnico para esto es impulso) contra la pared que las ligeras con la misma velocidad.

Finalmente, la ecuación nos dice que la presión es proporcional al promedio de los cuadrados de las velocidades moleculares. Esta dependencia del cuadrado de velocidad es razonable si nos damos cuenta de que duplicar la velocidad de una molécula tiene dos efectos.

En primer lugar, la molécula puede moverse más lejos en un período de tiempo determinado, duplicando el número de colisiones con las paredes. Esto duplicaría la presión. Segundo, duplicar la velocidad de una molécula duplica el empuje o impulso de cada colisión. Esto duplica la presión de nuevo. Por lo tanto, duplicar la velocidad de una molécula cuadruplica la presión, y para un gran número de moléculas, P es proporcional a la velocidad cuadrada media.