La Ley de Boyle
Robert Boyle (1627-1691), químico inglés, es ampliamente considerado como uno de los fundadores de la ciencia experimental moderna de la química. Descubrió que duplicar la presión de una muestra de gas encerrada mientras mantenía su temperatura constante hacía que el volumen del gas se redujera a la mitad. La ley de Boyle establece que el volumen de una masa dada de gas varía inversamente con la presión cuando la temperatura se mantiene constante. Una relación inversa se describe de esta manera. A medida que una variable aumenta de valor, la otra variable disminuye.
Físicamente, ¿qué está pasando? Las moléculas de gas se están moviendo y están a cierta distancia unas de otras. Un aumento de la presión empuja las moléculas más juntas, reduciendo el volumen. Si la presión disminuye, los gases pueden moverse libremente en un volumen mayor.

Matemáticamente, la ley de Boyle se puede expresar mediante la ecuación:
\
El \(k\) es una constante para una muestra dada de gas y sólo depende de la masa del gas y la temperatura. La siguiente tabla muestra datos de presión y volumen para una cantidad determinada de gas a temperatura constante. La tercera columna representa el valor de la constante \(\left (k \right)\) para estos datos y siempre es igual a la presión multiplicada por el volumen. A medida que una de las variables cambia, la otra cambia de tal manera que el producto de \(P \times V\) siempre permanece igual. En este caso particular, esa constante es \(500\: \ text{atm} \ cdot \ text {mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
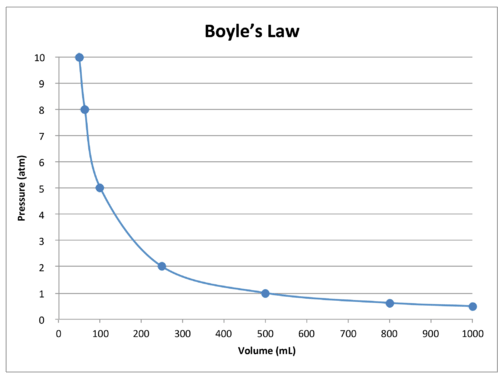
Un gráfico de los datos en la tabla ilustra la relación inversa de la naturaleza de la Ley de Boyle (ver figura de abajo). El volumen se representa en el eje \(x\), con la presión correspondiente en el eje \(y\).
La Ley de Boyle se puede usar para comparar las condiciones cambiantes de un gas. Usamos \(P_1\) y \(V_1\) para representar la presión inicial y el volumen inicial de un gas. Después de realizar un cambio, \(P_2\) y \(V_2\) representan la presión y el volumen finales. La relación matemática de la Ley de Boyle se convierte en:
\
Esta ecuación se puede usar para calcular cualquiera de las cuatro cantidades si se conocen las otras tres.
Ejemplo \(\pageIndex{1}\)
Una muestra de gas de oxígeno tiene un volumen de \(425 \: \text{mL}\) cuando la presión es igual a \(387 \: \text{kPa}\). Se permite que el gas se expanda en un contenedor \(1.75\: \ text{L}\). Calcule la nueva presión del gas.
Solución
Paso 1: Enumere las cantidades conocidas y planifique el problema.
Conocido
- \(P_1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1.75 \: \text{L} = 1750 \: \text{mL}\)
Desconocido
- \(P_2 = ? \ : \ text{kPa}\)
Use la Ley de Boyle para resolver la presión desconocida \(\left (P_2 \right)\). Es importante que los dos volúmenes (\(V_1\) y \(V_2\)) se expresen en las mismas unidades, de modo que \(V_2\) se haya convertido a \(\text{mL}\).
Paso 2: Resolver.
Primero, reorganiza la ecuación algebraicamente para resolver para \(P_2\).
\
Ahora sustituye las cantidades conocidas en la ecuación y resolver.
\
Paso 3: Piense acerca de su resultado.
El volumen ha aumentado a un poco más de 4 veces su valor original, por lo que la presión disminuye en aproximadamente un cuarto. La presión está en \(\text{kPa}\) y el valor tiene tres cifras significativas. Tenga en cuenta que cualquier unidad de presión o volumen se puede usar siempre y cuando sea consistente durante todo el problema.