koordinatplanet
læringsmål(er)
· Plot bestilt par på et koordinatplan.
· givet et ordnet par, bestem dets kvadrant.
introduktion
koordinatplanet blev udviklet for århundreder siden og raffineret af den franske matematiker ren Krist Descartes. Til hans ære kaldes systemet undertiden det kartesiske koordinatsystem. Koordinatplanet kan bruges til at plotte punkter og graflinjer. Dette system giver os mulighed for at beskrive algebraiske forhold i visuel forstand og hjælper os også med at skabe og fortolke algebraiske begreber.
Lær koordinatplanet at kende
du har sandsynligvis brugt et koordinatplan før. Har du for eksempel nogensinde brugt et gitteroverlay til at kortlægge placeringen af et objekt? (Dette gøres ofte med køreplaner, også.)

dette “kort” bruger et vandret og lodret gitter til at formidle information om et objekts placering. Bemærk, at bogstaverne A-F er angivet langs toppen, og tallene 1-6 er angivet langs venstre kant. Den generelle placering af ethvert element på dette kort kan findes ved hjælp af bogstavet og nummeret på dets gitterfirkant. For eksempel kan du finde det element, der findes ved firkant “4F” ved at flytte fingeren langs vandret til bogstav F og derefter lige ned, så du er på linje med 4. Du finder en blå disk er på dette sted på kortet.
koordinatplanet har lignende elementer som gitteret vist ovenfor. Den består af en vandret akse og en lodret akse, antal linjer, der skærer i rette vinkler. (De er vinkelret på hinanden.)
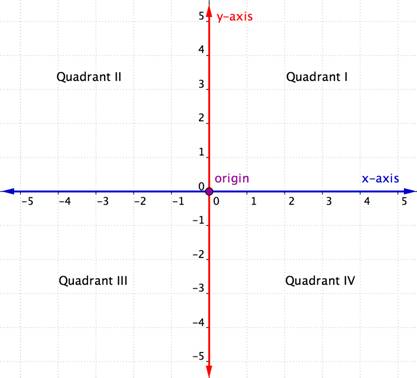
den vandrette akse i koordinatplanet kaldes h-aksen. Den lodrette akse kaldes y-aksen. Det punkt, hvor de to akser krydser hinanden, kaldes oprindelsen. Oprindelsen er på 0 på h-aksen og 0 på y-aksen.
de krydsende h – og y-akser deler koordinatplanet i fire sektioner. Disse fire sektioner kaldes kvadranter. Kvadranter navngives ved hjælp af romertal I, II, III og IV, der begynder med den øverste højre kvadrant og bevæger sig mod uret.
placeringer på koordinatplanet beskrives som ordnede par. Et ordnet par fortæller dig placeringen af et punkt ved at relatere punktets placering langs aksen (den første værdi af det ordnede par) og langs y-aksen (den anden værdi af det ordnede par).
i et ordnet par, f.eks. Bemærk, at koordinaten er angivet før y-koordinaten. Da oprindelsen har en røntgenkoordinat på 0 og en Y-koordinat på 0, skrives det bestilte par (0, 0).
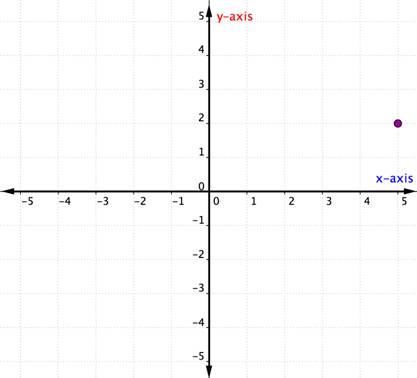
overvej nedenstående punkt.
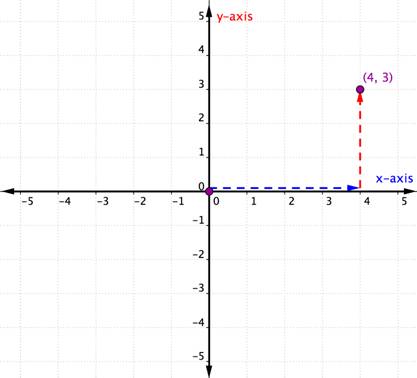
for at identificere placeringen af dette punkt skal du starte ved oprindelsen (0, 0) og bevæge dig til højre langs h-aksen, indtil du er under punktet. Se på etiketten på h-aksen. 4 angiver, at du fra oprindelsen har rejst fire enheder til højre langs h-aksen. Dette er koordinaten, det første nummer i det bestilte par.
fra 4 på h-aksen bevæger sig op til punktet og bemærker det nummer, som det justerer på y-aksen. 3 angiver, at du efter at have forladt h-aksen rejste 3 enheder op i lodret retning, retningen af y-aksen. Dette nummer er Y-koordinaten, det andet nummer i det bestilte par. Med en kn-koordinat på 4 og en y-koordinat på 3 Har du det bestilte par (4, 3).
lad os se på et andet eksempel.
|
Example |
||
|
Problem |
Describe the point shown as an ordered pair. |
|
|
|
||
|
(5, y) |
Begynd ved oprindelsen og bevæg dig langs h-aksen. Dette er koordinaten og skrives først i det bestilte par. |
|
|
(5, 2) |
Flyt fra 5 op til det bestilte par og læs nummeret på Y-aksen. Dette er Y-koordinaten og er skrevet andet i det bestilte par. |
|
|
svar |
punktet vist som et bestilt par er (5, 2). |
|
plotte punkter i koordinatplanet
nu hvor du ved, hvordan du bruger H – og Y-akserne, kan du også plotte et ordnet par. Bare husk, begge processer starter ved oprindelsen-begyndelsen! Eksemplet, der følger, viser, hvordan man tegner det bestilte par (1, 3).
|
Example |
||
|
Problem |
Plot the point (1, 3). |
|
|
|
||
|
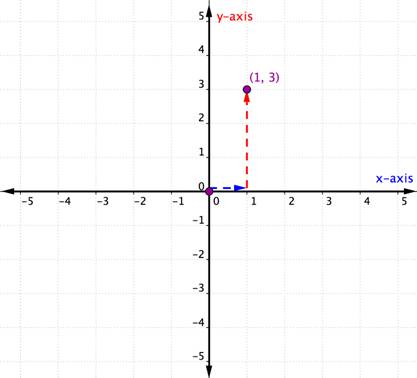
The x-coordinate is 1 because it comes first in the ordered pair. Start ved oprindelsen og flyt en afstand på 1 enhed i en positiv retning (til højre) fra oprindelsen langs h-aksen. |
y-koordinaten er 3, fordi den kommer anden i det bestilte par. Herfra flytte direkte 3 enheder i en positiv retning (op). Hvis du kigger over til y-aksen, skal du være linet op med 3 på den akse. |
|
|
svar |
Tegn et punkt på dette sted og mærke punktet (1, 3). |
|
i det foregående eksempel var både K – og y-koordinaterne positive. Når en (eller begge) af koordinaterne for et ordnet par er negativ, skal du bevæge dig i negativ retning langs en eller begge akser. Overvej eksemplet nedenfor, hvor begge koordinater er negative.
|
Example |
||
|
Problem |
Plot the point (−4, −2). |
|
|
|
||
|
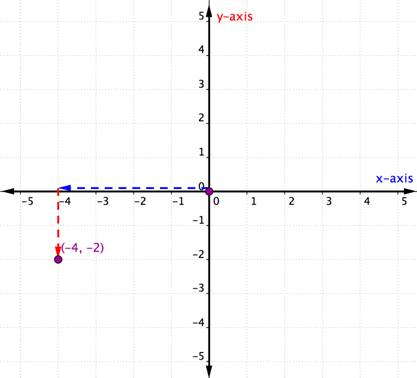
The x-coordinate is −4 because it comes first in the ordered pair. Start ved oprindelsen og flyt 4 enheder i en negativ retning (venstre) langs h-aksen. |
y-koordinaten er -2, fordi den kommer anden i det bestilte par. Flyt nu 2 enheder i negativ retning (ned). Hvis du kigger over til y-aksen, skal du være linet op med -2 på den akse. |
|
|
svar |
Tegn et punkt på dette sted og mærke punktet (-4, -2). |
|
trinene til planlægning af et punkt er opsummeret nedenfor.
trin til planlægning af et ordnet par (h, y) i koordinatplanet
O Bestem k-koordinaten. Begynd ved oprindelsen, bevæg dig vandret, retningen af H-aksen, afstanden givet af H-koordinaten. Hvis koordinaten er positiv, skal du flytte til højre; hvis koordinaten er negativ, skal du flytte til venstre.
O Bestem y-koordinaten. Begynd ved koordinaten, bevæg dig lodret, retningen af y-aksen, afstanden givet af y-koordinaten. Hvis Y-koordinaten er positiv, skal du gå op; hvis Y-koordinaten er negativ, skal du flytte ned.
O Tegn et punkt på slutningsstedet. Mærk punktet med det bestilte par.
hvilket punkt repræsenterer det bestilte par (-2, -3)?
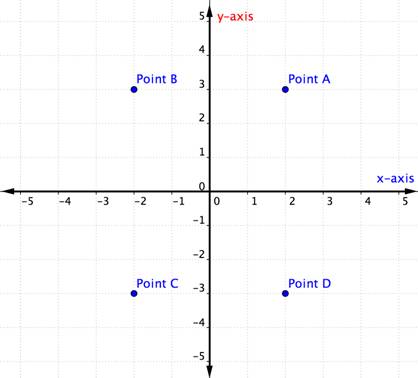
de fire kvadranter
bestilte par inden for en bestemt kvadrant deler visse egenskaber. Se på hver kvadrant i grafen nedenfor. Hvad bemærker du om tegnene på K-og Y-koordinaterne for punkterne inden for hver kvadrant?
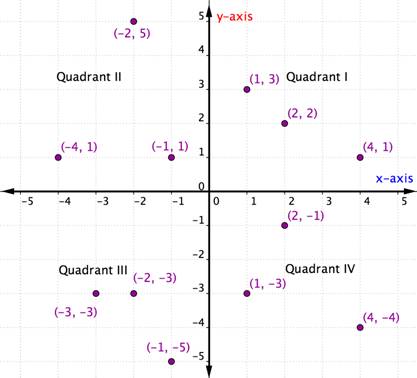
inden for hver kvadrant er tegnene på koordinaterne og Y-koordinaterne for hvert ordnet par de samme. De følger også et mønster, som er skitseret i nedenstående tabel.
når du ved om kvadranterne i koordinatplanet, kan du bestemme kvadranten for et ordnet par uden selv at tegne det ved at se på diagrammet ovenfor. Her er en anden måde at tænke over det.
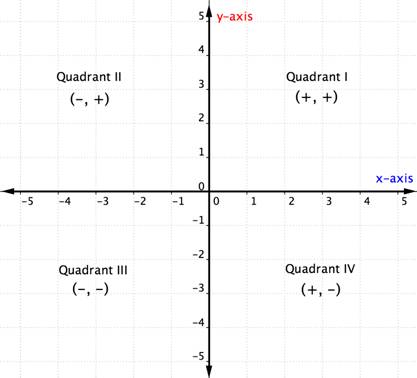
eksemplet nedenfor beskriver, hvordan man bestemmer kvadrantplaceringen af et punkt bare ved at tænke på tegnene på dets koordinater. At tænke på kvadrantplaceringen, før du planlægger et punkt, kan hjælpe dig med at forhindre en fejl. Det er også nyttig viden til at kontrollere, at du har tegnet et punkt korrekt.
Hvad sker der, hvis et ordnet par har en H – eller y-koordinat på nul? Eksemplet nedenfor viser grafen for det bestilte par (0, 4).
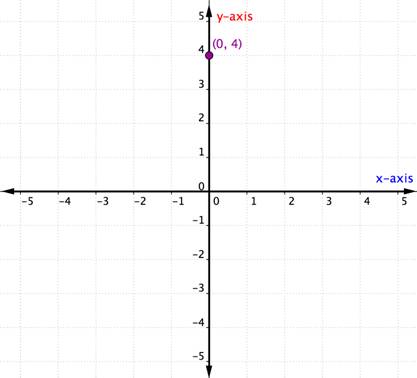
et punkt placeret på en af akserne anses ikke for at være i en kvadrant. Det er simpelthen på en af akserne. Når koordinaten er 0, er punktet placeret på Y-aksen. Tilsvarende vil ethvert punkt, der har en Y-koordinat på 0, være placeret på h-aksen.
hvilken af beskrivelserne nedenfor beskriver bedst placeringen af punktet (8, 0)?
A) kvadrant i
B) Det er på h-aksen
C) det er på y-aksen
D) koordinatplanet
Resume
koordinatplanet er et system til at tegne og beskrive punkter og linjer. Koordinatplanet består af en vandret (h-) akse og en lodret (y-) akse. Skæringspunktet mellem disse linjer skaber oprindelsen, som er punktet (0, 0). Koordinatplanet er opdelt i fire kvadranter. Sammen giver disse funktioner i koordinatsystemet mulighed for grafisk repræsentation og kommunikation om punkter, linjer og andre algebraiske begreber.