nogle interessante ting om vinkler og cirkler.
- indskrevet vinkel
- indskrevne Vinkelteoremer
- eksempel: Hvad er størrelsen af Vinkelpok? (O er cirkelens centrum)
- eksempel: Hvad er størrelsen af vinkel CB?
- en anden god grund til, at det virker
- eksempel: Hvad er størrelsen af vinkel BAC?
- Find en cirkels Center
- cyklisk firkant
- eksempel: Hvad er størrelsen af vinkel?
indskrevet vinkel
først ud, en definition:
indskrevet vinkel: en vinkel lavet af punkter, der sidder på cirkelens omkreds.
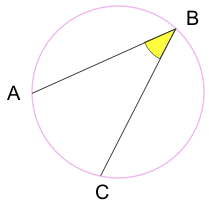
A og C er “slutpunkter”
B er “toppunktet”
leg med det her:
Når du flytter punkt “B”, Hvad sker der med vinklen?
indskrevne Vinkelteoremer
en indskrevet vinkel a-bogstav er halvdelen af den centrale vinkel 2a-bogstav
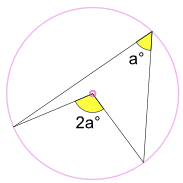
(kaldet vinklen i midten sætning)
og (holder slutpunkterne faste) …
… vinklen a-kursen er altid den samme,
uanset hvor den er på den samme bue mellem endepunkter:
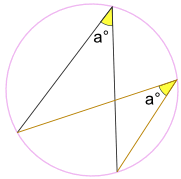
vinkel A-kursen er den samme.
(kaldet vinklerne Subtended af samme bue sætning)
eksempel: Hvad er størrelsen af Vinkelpok? (O er cirkelens centrum)
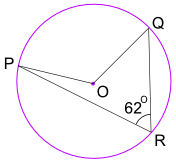
Vinkelpok = 2= 2 × 62° = 124°
eksempel: Hvad er størrelsen af vinkel CB?
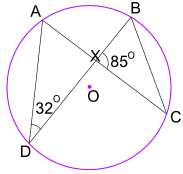
vinkel ADB = 32 purpur er også lig med Vinkel ACB.
og vinkel ACB er også lig med Vinkel.
så i trekant BHC kender vi vinkel BHC = 85 liter, og vinkel BH = 32 liter
brug nu vinkler af en trekant Tilføj til 180 liter :
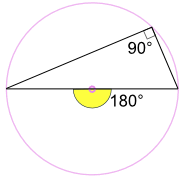
en vinkel indskrevet på tværs af en cirkels diameter er altid en ret vinkel:
(endepunkterne er begge ender af en cirkels diameter,
toppunktet kan være hvor som helst på den anden side af en cirkel omkreds.)
|
hvorfor? Fordi: den indskrevne vinkel 90 lit er halvdelen af den centrale vinkel 180 lit (Ved hjælp af “vinkel ved Midtersætningen” ovenfor) |
 |
en anden god grund til, at det virker
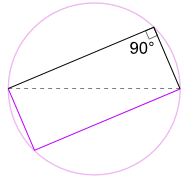
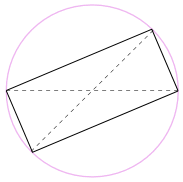
Vi kunne også rotere formen rundt om en cirkel, der ikke er mere end 180 til at lave et rektangel!
det er et rektangel, fordi alle sider er parallelle, og begge diagonaler er ens.
og så er dens indre vinkler alle rette vinkler (90 liter).
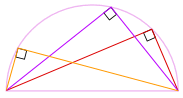
så der går vi! Uanset hvor den vinkel er
på omkredsen, er den altid 90 liter
eksempel: Hvad er størrelsen af vinkel BAC?
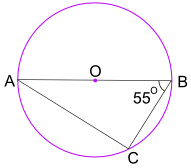
vinklen i Halvcirkelsætningen fortæller os, at vinkel ACB = 90 liter
brug nu vinkler af en trekant Tilføj til 180 liter for at finde vinkel BAC:
Find en cirkels Center
Vi kan bruge denne ide til at finde en cirkels center:
- tegn en ret vinkel fra hvor som helst på cirkelens omkreds, træk derefter diameteren, hvor de to ben rammer cirklen
- gør det igen, men for en anden diameter
hvor diameterne krydser er midten!
cyklisk firkant
|
en “cyklisk” firkant har hvert toppunkt på en cirkels omkreds: |
 |
|
en cyklisk firkant ‘ s modsatte vinkler Tilføj til 180 liter:
|
 |
eksempel: Hvad er størrelsen af vinkel?
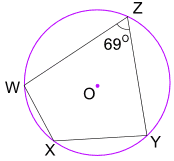
Opposite angles of a cyclic quadrilateral add to 180°

