- Cíle Vzdělávání
- práce proti gravitaci
- Převod Mezi Potenciální Energie a Kinetická Energie
- Použití Potenciální Energie pro Zjednodušení Výpočtů
- Příklad 1. Síla k zastavení pádu
- strategie
- Řešení
- Diskuse
- příklad 2. Zjištění Rychlosti na Horské Dráze z jeho Výška
- strategie
- řešení pro Část 1
- Řešení pro Část 2
- diskuse a důsledky
- Připojení: Take-Home Šetření—Přeměny Potenciální na Kinetickou Energii
- shrnutí sekce
- Koncepční Otázky
- Problémy & Cvičení
- Slovníček pojmů
- Vybrané Řešení Problémů & Cvičení
Cíle Vzdělávání
na konci této části, budete moci:
- Vysvětlit gravitační potenciální energie, pokud jde o práci proti gravitaci.
- ukazují, že gravitační potenciální energie objektu o hmotnosti m ve výšce h na Zemi je dána PEg = mgh.
- ukažte, jak lze znalost potenciální energie jako funkce polohy použít ke zjednodušení výpočtů a vysvětlení fyzikálních jevů.
práce proti gravitaci
lezení po schodech a zvedání předmětů je práce ve vědeckém i každodenním smyslu-je to práce proti gravitační síle— Když je práce, dochází k transformaci energie. Práce provedená proti gravitační síle jde do důležité formy uložené energie, kterou prozkoumáme v této části.

Obrázek 1. a) práce vykonaná při zvedání hmotnosti je uložena v systému hmota-země jako gravitační potenciální energie. b) při pohybu hmotnosti směrem dolů se tato gravitační potenciální energie přenáší na kukačkové hodiny.
vypočítejme práci provedenou při zvedání objektu o hmotnosti m do výšky h, například na obrázku 1. Pokud je předmět zvednut rovně nahoru konstantní rychlostí, pak síla potřebná k jeho zvedání se rovná jeho hmotnosti mg. Práce na hmotě je pak W = Fd = mgh. Definujeme to jako gravitační potenciální energii (PEg) vloženou do (nebo získanou) systému objekt-země. Tato energie je spojena se stavem oddělení mezi dvěma objekty, které se navzájem přitahují gravitační silou. Pro větší pohodlí to označujeme jako kolík získaný objektem, který uznává, že se jedná o energii uloženou v gravitačním poli Země. Proč používáme slovo „systém“? Potenciální energie je vlastností systému spíše než jediného objektu-kvůli jeho fyzické poloze. Gravitační potenciál objektu je způsoben jeho polohou vzhledem k okolí v systému země-objekt. Síla působící na objekt je vnější síla zvenčí systému. Když to dělá pozitivní práci, zvyšuje gravitační potenciální energii systému. Protože gravitační potenciální energie závisí na relativní poloze, potřebujeme referenční úroveň, na které nastavíme potenciální energii rovnou 0. Tento bod obvykle volíme jako zemský povrch, ale tento bod je libovolný; důležitý je rozdíl v gravitační potenciální energii, protože tento rozdíl souvisí s provedenou prací. Rozdíl v gravitační potenciální energii objektu (v systému země-objekt) mezi dvěma příčkami žebříku bude stejný pro první dvě příčky jako pro poslední dvě příčky.
Převod Mezi Potenciální Energie a Kinetická Energie
Gravitační potenciální energie může být přeměněna na jiné formy energie, např. kinetickou energii. Pokud uvolníme hmotu, gravitační síla na ní provede množství práce rovnající se mgh, čímž zvýší její kinetickou energii o stejné množství (větou o pracovní energii). Považujeme za užitečnější zvážit pouze konverzi PEg na KE, aniž bychom výslovně zvážili mezistupeň práce. (Viz Příklad 2.) Tato zkratka usnadňuje řešení problémů pomocí energie (pokud je to možné) spíše než explicitně pomocí sil.
přesněji, definujeme změna gravitační potenciální energie ΔPEg být ΔPEg = mgh, kde pro jednoduchost označme změnu výšky h, spíše než obvyklý Δh. Všimněte si, že h je pozitivní, když je konečná výška větší než počáteční výška a naopak. Například, pokud se zvýší hmotnost 0,500 kg zavěšená na kukačkových hodinách 1.00 m, pak jeho změna gravitační potenciální energie,
\begin{array}{lll}mgh&&(0.500\text{ kg})(9.80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\text {/}^2=4.90\text{ J}\end{array}\\
Všimněte si, že jednotky gravitační potenciální energie se ukáže být joulů, stejně jako pro práci a jiné formy energie. Jak hodiny běží, hmotnost se sníží. Můžeme si myslet, že hmota se postupně vzdává svých 4.90 J gravitační potenciální energie, bez přímého zvážení gravitační síly, která dělá práci.
Použití Potenciální Energie pro Zjednodušení Výpočtů

Obrázek 2. Změna gravitační potenciální energie (ΔPEg) mezi body a A B je nezávislá na dráze.
rovnice ΔPEg = mgh platí pro jakoukoli dráhu, která má změnu výšky h, nejen když je hmota zvednuta rovně nahoru. (Viz Obrázek 2.) Je mnohem snazší vypočítat mgh (jednoduché násobení), než je vypočítat práci provedenou po složité cestě. Myšlenka gravitační potenciální energie má dvojí výhodu, že je velmi široce použitelná a usnadňuje výpočty.
Od teď, budeme uvažovat, že každá změna ve svislé poloze h a hmotnosti m je doprovázena změnou v gravitační potenciální energii mgh, a my se vyhnout ekvivalent, ale obtížnější úkol výpočtu práce, kterou nebo proti gravitační síle.
ΔPEg = mgh pro jakoukoli cestu mezi dvěma body. Gravitace je jedním z malé třídy sil, kde se práce provádí, nebo proti síle závisí pouze na počáteční a koncové body, ne na cestu mezi nimi.
Příklad 1. Síla k zastavení pádu
a 60.0-kg člověk skočí na zem z výšky 3,00 m. Pokud přistane toporně (s jeho kolenní klouby kompresí tím 0.500 cm), výpočet síly na kolenní klouby.
strategie
energie této osoby je v této situaci přivedena na nulu prací, kterou na něm provádí podlaha, když se zastaví. Počáteční kolík se při pádu přemění na KE. Práce na podlaze snižuje tuto kinetickou energii na nulu.
Řešení
práce na osobu podlaze, jak on se zastaví, je dána vztahem W = Fd cos θ = −Fd, se znaménkem minus, protože posunutí při zastavení a síla od podlahy jsou v opačných směrech (cos θ = cos 180 ° = -1). Podlaha odstraňuje energii ze systému, takže dělá negativní práci.
kinetická energie, kterou má člověk po dosažení podlahy, je množství potenciální energie ztracené pádem výškou h: ke = – ΔPEg = −mgh.
vzdálenost d, že osoba, kolena ohnout, je mnohem menší, než je výška h pádu, takže další změna gravitační potenciální energie během koleno ohnout je ignorována.
práce, kterou provádí podlaha na osobě, zastaví osobu a přinese kinetickou energii osoby na nulu: W = – ke = mgh.
kombinace této rovnice s výrazem pro W dává-Fd = mgh.
Připomenout, že h je negativní, protože člověk padl, síly na kolenní klouby, je dána tím,
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\right)\left(9.80\text{ m/s}^2\right)\left(-3.00\text{ m}\right)}{5.00\krát 10^{-3}\text{ m}}=3.53\krát 10^5\text{ N}\\
Diskuse
Tak velké síly (500 krát více, než je hmotnost člověka) během krátkého času dopadu je dost, aby zlomit kosti. Mnohem lepší způsob, jak tlumit šok, je ohýbání nohou nebo válcování na zemi, čímž se prodlužuje doba, po kterou síla působí. Ohybový pohyb 0,5 m tímto způsobem získá sílu 100krát menší než v příkladu. Klokanův skok ukazuje tuto metodu v akci. Klokan je jediný živočich, pro použití hopping pro pohyb, ale šok v plovoucím je čalouněná tím, ohýbání zadních nohou v každém skoku. (Viz Obrázek 3.)

obrázek 3. Práce vykonaná zemí na klokanu snižuje jeho kinetickou energii na nulu, když přistane. Avšak působením síly země na zadní nohy na delší vzdálenost se sníží dopad na kosti. (kredit: Chris Samuel, Flickr)
příklad 2. Zjištění Rychlosti na Horské Dráze z jeho Výška
- Co je konečná rychlost na horské dráze je znázorněno na Obrázku 4, pokud začíná z klidu na vrcholu 20.0 m hill a práce třecí síly je zanedbatelný?
- jaká je jeho konečná rychlost (opět za předpokladu zanedbatelného tření), pokud je její počáteční rychlost 5,00 m/s?
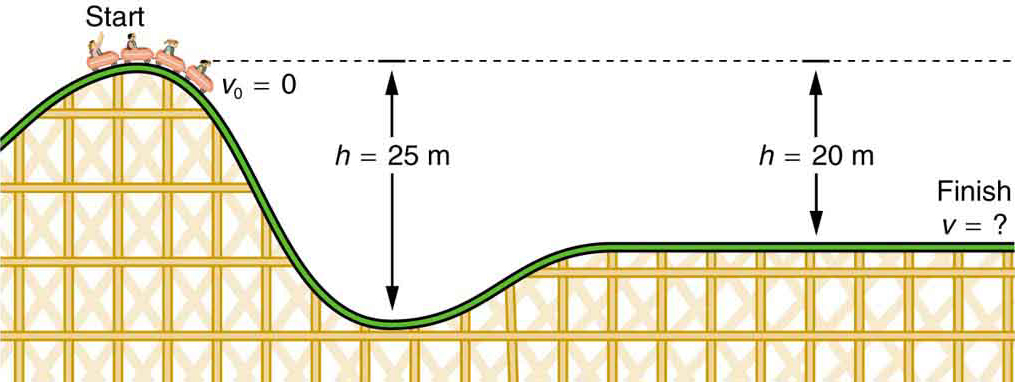
obrázek 4. Rychlost horské dráhy se zvyšuje, jak ji gravitace táhne z kopce a je největší v nejnižším bodě. Při pohledu na energii je gravitační potenciální energie systému horská dráha-Země přeměněna na kinetickou energii. Pokud je práce prováděná třením zanedbatelná, převede se veškerý ΔPEg na KE.
strategie
horská dráha při sjezdu ztrácí potenciální energii. Zanedbáváme tření, tak, aby zbývající síla, kterou působí trati je normálová síla, která je kolmá ke směru pohybu a nemá žádnou práci. Čistá práce na horské dráze se pak provádí pouze gravitací. Ztráta gravitační potenciální energie z pohybu směrem dolů ve vzdálenosti h se rovná zisku kinetické energie. To lze zapsat ve formě rovnice jako-ΔPEg = ΔKE. Pomocí rovnic pro PEg a KE můžeme vyřešit konečnou rychlost v, což je požadované množství.
řešení pro Část 1
zde je počáteční kinetická energie nulová, takže \Delta \ text{KE}=\frac{1}{2}mv^2\\. Rovnice pro změnu potenciální energie uvádí, že ΔPEg = mgh. Protože h je v tomto případě záporné, přepíšeme to jako ΔPEg = – mg / h|, abychom jasně ukázali znaménko mínus. Takže-ΔPEg = ΔKE se stává mg / h / = \ frac{1}{2}{mv}^2\\.
řešení pro v, zjistíme, že hmotnost ruší a že v= \ sqrt{2g / h/}\\.
po Dosazení známých hodnot,
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
Řešení pro Část 2
Znovu −ΔPEg = ΔKE. V tomto případě je počáteční kinetické energie,
\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
tedy mg / h/= \ frac{1}{2}mv^2 – \frac{1}{2}mv_0^2\\.
přeskupení dává \ frac{1}{2}mv^2=mg / h / + \ frac{1}{2}mv + 0^2\\.
to znamená, že konečná kinetická energie je součtem počáteční kinetické energie a gravitační potenciální energie. Hmotnost se opět zruší a v=\sqrt{2g|h / +v_0^2}\\.
Tato rovnice je velmi podobná rovnice kinematiky v=\sqrt{v_0^2+2ad}\\, ale to je obecnější—kinematika, rovnice je platná pouze pro konstantní zrychlení, vzhledem k tomu, že naše rovnice je platná pro jakoukoli cestu, bez ohledu na to, zda se objekt pohybuje s konstantním zrychlením. Nyní, dosazením známých hodnot dává
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left(5.00\text{ m/s}\right)^2}\\\text{ }&&20.4 \ text{ m / s} \ end{array}\\
diskuse a důsledky
nejprve si všimněte, že hmotnost se ruší. To je zcela v souladu s pozorováním u padajících předmětů, že všechny objekty padají stejnou rychlostí, pokud je tření zanedbatelné. Za druhé, zvažuje se pouze rychlost horské dráhy, v žádném okamžiku neexistují žádné informace o jejím směru. To odhaluje další obecnou pravdu. Při tření je zanedbatelné, rychlost padající tělo, závisí pouze na jeho počáteční rychlosti a výšce, a nikoli na jeho hmotnosti nebo cesta přijata. Například horská dráha bude mít stejné konečné rychlosti ať to padá 20.0 m rovně dolů nebo má složitější cestu, jako ten na obrázku. Třetí, a možná nečekaně, konečná rychlost v části 2 je větší než v části 1, ale daleko méně než 5,00 m/s. A konečně, na vědomí, že rychlost lze nalézt v jakékoliv výšce podél způsob, jak jednoduše pomocí odpovídající hodnota h na bod zájmu.
Jsme viděli, že práce, kterou nebo proti gravitační síla závisí jen na počáteční a koncové body, a ne na cestě mezi, což nám umožňuje definovat zjednodušení pojem gravitační potenciální energie. Můžeme udělat totéž pro několik dalších sil a uvidíme, že to vede k formální definici zákona zachování energie.
Připojení: Take-Home Šetření—Přeměny Potenciální na Kinetickou Energii
Jeden může studovat přeměnu gravitační potenciální energie na kinetickou energii v tomto experimentu. Na hladkém, rovném povrchu použijte pravítko typu, které má podél své délky drážku a knihu, abyste vytvořili sklon (viz obrázek 5). Umístěte mramor do polohy 10 cm na pravítko a nechte jej převrátit pravítkem. Když narazí na rovný povrch, změřte čas potřebný k převrácení jednoho metru. Nyní umístěte mramor do polohy 20 cm a 30 cm a znovu změřte dobu potřebnou k převrácení 1 m na rovný povrch. Najděte rychlost mramoru na rovném povrchu pro všechny tři polohy. Rychlost spiknutí na druhou oproti vzdálenosti ujeté mramorem. Jaký je tvar každého pozemku? Pokud je tvar přímka, graf ukazuje, že kinetická energie mramoru ve spodní části je úměrná jeho potenciální energii v bodě uvolnění.

obrázek 5. Mramor se valí po pravítku a měří se jeho rychlost na rovném povrchu.
shrnutí sekce
- práce vykonaná proti gravitaci při zvedání objektu se stává potenciální energií systému objekt-země.
- změna gravitační potenciální energie, ΔPEg, je ΔPEg = mgh, kde h je zvýšení výšky a g tíhové zrychlení.
- gravitační potenciální energie objektu v blízkosti zemského povrchu je způsobena jeho polohou v systému hmota-země. Pouze rozdíly v gravitační potenciální energii, ΔPEg, mají fyzický význam.
- Jako objekt sestupuje bez tření, jeho gravitační potenciální energie mění na kinetickou energii odpovídající zvyšující se rychlostí, tak, že ΔKE = −ΔPEg
Koncepční Otázky
- V Příkladu 2, jsme spočítali, konečná rychlost na horské dráze, která sestoupila 20 m na výšku a měl počáteční rychlost 5 m/s kopce. Předpokládám, že horská dráha měla počáteční rychlost 5 m/s do kopce místo, a to dobíhá do kopce, zastavil se, a pak se vrátit zpět dolů do konečného bodu 20 m pod start. V tom případě bychom zjistili, že má stejnou konečnou rychlost. Vysvětlete, pokud jde o zachování energie.
- závisí práce, kterou děláte na knize, když ji zvednete na polici, na zvolené cestě? Na čas? Na výšku police? O hmotnosti knihy?
Problémy & Cvičení
- vodní elektrárny (viz Obrázek 6) převádí gravitační potenciální energie vody za přehradou na elektrickou energii. a) jaká je gravitační potenciální energie vzhledem k generátorům jezera o objemu 50.0 km3 (hmotnost = 5,00 × 1013 kg), vzhledem k tomu, že jezero má průměrnou výšku 40,0 m nad generátory? b) srovnejte to s energií uloženou v 9megatonové fúzní bombě.

obrázek 6. Vodní zařízení (credit: Denis Ruské, Wikimedia Commons)
- (a) Jak velkou gravitační potenciální energie (vzhledem k zemi, na kterých je postaven) je uložen v cheopsovy Pyramidy, vzhledem k tomu, že jeho hmotnost je asi 7 × 109 kg a jeho těžiště je 36.5 m nad okolní zemí? b) jak se tato energie porovnává s denním příjmem potravy člověka?
- Předpokládejme, že 350 g kookaburra (velký ledňáček) zvedne 75 g hada a zvedne ho 2,5 m od země k větvi. a) kolik práce udělal pták na hada? b) kolik práce odvedla, aby se do pobočky dostalo vlastní těžiště?
- v příkladu 2 jsme zjistili, že rychlost horské dráhy, která sestoupila 20,0 m, byla jen o něco větší, když měla počáteční rychlost 5,00 m / s, než když začala z klidu. To znamená, že ΔPE >> KEi. Potvrďte toto tvrzení poměrem ΔPE ke KEi. (Všimněte si, že mass ruší.)
- 100-g autíčko je poháněno stlačenou pružinou, která ho nastartuje do pohybu. Vůz sleduje zakřivenou stopu na obrázku 7. Ukázat, že konečná rychlost autíčka je 0.687 m/s, jestliže jeho počáteční rychlost je 2,00 m/s a to pobřeží se tření svahu, získává 0.180 m nadmořské výšky.

Obrázek 7. Autíčko se pohybuje po šikmé dráze. (kredit: Leszek Leszczynski, Flickr)
- v závodě sjezdového lyžování se překvapivě získává malá výhoda získáním běžeckého startu. (Je to proto, že počáteční kinetická energie je malá ve srovnání se ziskem gravitační potenciální energie na i malých kopcích.) Prokázat to, najít konečnou rychlost a čas potřebný pro lyžaře, kteří nebe 70.0 m po 30º sklon zanedbání tření: (a) od zbytku. (b) počínaje počáteční rychlostí 2,50 m / s. (c) překvapuje vás odpověď? Diskutujte o tom, proč je stále výhodné začít s velmi konkurenčními událostmi.
Slovníček pojmů
gravitační potenciální energie: energie, objekt má díky své poloze v gravitačním poli,
Vybrané Řešení Problémů & Cvičení
1. a) 1,96 × 1016 J; B) poměr gravitační potenciální energie v jezeře k energii uložené v bombě je 0,52. To znamená, že energie uložená v jezeře je přibližně polovina energie v 9 megatunové fúzní bombě.
3. a) 1,8 J; b) 8,6 j
5. {v}_{f}=\sqrt{2gh+{v_0}^2}=\sqrt{2\left(9.80\text{ m/s}^2\right)\left(-0.180\text{ m}\right)+\left(2.00\text{ m/s}\right)^2}=0.687\text{ m/s}\\