Po pochopení exponenciální funkce, náš další cíl je přirozený logaritmus.

vzhledem k tomu, jak je přirozený log popsán v matematických knihách, je o něm málo „přirozeného“: je definován jako inverzní hodnota $E^x$, což je již dost podivný exponent.

ale je tu čerstvé, intuitivní vysvětlení: přirozený protokol vám dává čas potřebný k dosažení určité úrovně růstu.

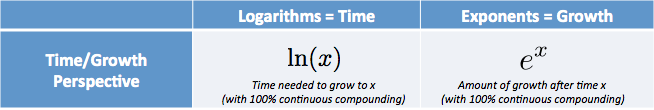
Předpokládejme, že máte investici do gumových medvědů (kdo ne?) s úrokovou sazbou 100% ročně, která neustále roste. Pokud chcete růst 10x za předpokladu nepřetržitého míchání, čekali byste pouze $\ln (10)$ nebo 2.302 let. Nechápu, proč to trvá jen několik let, aby si 10x růst? Nechápu, proč ten vzor není 1, 2, 4, 8? Přečtěte si více o e.

e a přirozený protokol jsou dvojčata:

• $e^x$ je částka, kterou máme po spuštění na 1.0 a neustále roste na $x$ jednotky času
• $\ln(x)$ (Přirozený Logaritmus), je čas k dosažení částky $x$, za předpokladu, že bychom rostla nepřetržitě od 1.0

to Není špatný, ne? Zatímco matematici se snaží poskytnout vám dlouhé, technické vysvětlení, pojďme se ponořit do intuitivního.

E je o růstu

číslo e je o nepřetržitém růstu. Jak jsme viděli minule, $e^x$ nám umožňuje sloučení rychlost a čas: 3 roky na 100% růst je stejný jako 1 rok na 300% růstu, když se neustále zhoršuje.

můžeme vzít libovolnou kombinaci rychlosti a času (50% po dobu 4 let) a převést sazbu na 100% pro pohodlí (což nám dává 100% po dobu 2 let). Převedením na 100%, jsme jen přemýšlet o době, kdy součásti:

Intuitivně, $e^x$ znamená:

• Jak růst, mohu dostat po x jednotek času (a 100% kontinuální růst)
• Pro příklad: po 3 obdobích mám $e^3$ = 20.08 krát množství „věci“.

$e^x$ je škálovací faktor, který nám ukazuje, kolik růstu bychom získali po $x$ jednotek času.

přirozený Log je o čase

přirozený log je inverzní hodnota $E^x$, což je efektní výraz pro opak. Když už mluvíme o Fantazie, latinský název je logaritmus naturali, dávat zkratku ln.

Co znamená tato inverzní nebo opačná věc?

• $e^x$ nám umožňuje zapojit čas a získat růst.
• $\ln (x)$ nám umožňuje zapojit růst a získat čas, který by to trvalo.

například:

• $e^3$ je 20.08. Po 3 jednotkách času skončíme s 20.08 krát to, s čím jsme začali.
• $\ln (20.08)$ je asi 3. Pokud chceme růst 20,08, počkáme 3 jednotky času (opět za předpokladu 100% nepřetržitého tempa růstu).

se mnou? Přirozený log nám dává čas potřebný k dosažení našeho požadovaného růstu.

logaritmická aritmetika není normální

už jste studovali protokoly a byly to podivné bestie. Jak proměnili násobení v sčítání? Rozdělení na odčítání? Podívejme se.

Co je $\ln (1)$? Intuitivně je otázka: jak dlouho čekám, až dostanu 1x svou aktuální částku?

nula. Zip. Naďa. Jste již na 1x své aktuální částky! Růst z 1 na 1 netrvá dlouho.

• $\ln(1) = 0$

Ok, co takhle zlomková hodnota? Jak dlouho se dostat 1/2 mé aktuální částky? Za předpokladu, že neustále rostete na 100%, víme, že $\ln (2)$ je množství času na zdvojnásobení. Vezmeme-li záporný čas), měli bychom polovinu naší současné hodnoty.

• $\ln (.5) = – \ln (2) = -.693$

dává smysl, že? Pokud půjdeme pozpátku .693 jednotek (záporných sekund, řekněme) bychom měli polovinu naší současné částky. Obecně můžete zlomek převrátit a vzít negativní: $\ln (1/3) = – \ln (3) = -1,09$. To znamená, že kdybychom se vrátili o 1,09 jednotky času, měli bychom třetinu toho, co máme nyní.

Ok, co takhle přirozený logaritmus záporného čísla? Kolik času trvá „růst“ kolonie bakterií od 1 do -3?

je to nemožné! Nemůžete mít „negativní“ množství bakterií, že? Nanejvýš (er… nejméně) můžete mít nulu, ale neexistuje žádný způsob, jak mít záporné množství malých zvířátek. Negativní bakterie prostě nedává smysl.

• $\ln (\text{záporné číslo}) = \text{undefined}$

Undefined znamená pouze „není čas, který můžete čekat“, abyste získali zápornou částku. (Pokud použijeme imaginární exponenciály, existuje řešení. Ale dnes to udržme skutečné.)

logaritmické násobení je mocná Zábava

Jak dlouho trvá růst 9x vaší aktuální částky? Jistě, mohli bychom použít ln (9). Ale to je příliš snadné, buďme jiní.

můžeme považovat růst 9x za ztrojnásobení (přičemž $\ln (3)$ jednotky času) a pak ztrojnásobení (přičemž další $\ln (3)$ jednotky času):

• čas na růst 9x = $ \ln (9)$ = čas na triple A triple again = $\ln (3) + \ln (3)$

zajímavé. Jakékoli číslo růstu, jako 20, lze považovat za 2x růst následovaný 10x růstem. Nebo 4x růst následovaný 5x růstem. Nebo 3x růst následovaný růstem 6.666 x. Vidíš ten vzor?

• $\ln (a*b) = \ln (a) + \ln (b)$

log a krát B = log(a) + log (b). Tento vztah má smysl, když si myslíte, že z hlediska času na růst.

Pokud chceme růst 30x, můžeme počkat $\ln (30)$ najednou, nebo jednoduše počkat $ \ ln (3)$, až se ztrojnásobí, pak počkat $\ln (10)$, abychom znovu rostli 10x. Čistý efekt je stejný ,takže čistý čas by měl být stejný (a to je).

a co dělení? $\ln (5/3)$ znamená: Jak dlouho trvá růst 5krát a pak to trvá 1/3?

no, růst 5 krát je $\ln (5)$. Rostoucí 1/3 je $-\ln (3)$ jednotky času. Takže

• $\ln(5/3) = \ln (5 – – \ln (3)$

který říká: růst 5krát a „vrátit se v čase“, dokud nebudete mít třetinu této částky, takže vám zůstane růst 5/3. Obecně máme

• $\ln (a/b) = \ln(a) – \ln (b)$

doufám, že podivná matematika logaritmů začíná dávat smysl: násobení růstu se stává přidáním času, dělení růstu se stává odečtením času. Nezapamatujte si pravidla, pochopte je.

pomocí přirozených protokolů s libovolnou rychlostí

„jistě,“ říkáte, “ tento protokol funguje pro 100% růst, ale co 5%, které normálně dostávám?“

není to žádný problém. „Čas“, který dostaneme zpět z $\ln ()$, je ve skutečnosti kombinací rychlosti a času, “ x “ z naší rovnice $E^x$. Jen předpokládáme 100%, aby to bylo jednoduché, ale můžeme použít jiná čísla.

Předpokládejme, že chceme růst 30x: připojte $\ln (30)$ a získejte 3.4. TED:

• $e^x = \text{růst}$
• $e^{3.4} = 30$

A intuitivně tato rovnice znamená „100% návratnost za 3,4 roky je 30x růst“. Můžeme uvažovat rovnici:

můžeme změnit „rychlost“ a „čas“, dokud rychlost * čas = 3.4. Předpokládejme například, že chceme růst 30x-jak dlouho budeme čekat za předpokladu 5% návratnosti —

• $\ln(30) = 3.4$
• $ \ text{rate} * \text{time} = 3.4$
• $.05 * \text{time} = 3.4$
• $\text{time} = 3.4 / .05 = 68 \ text{years} $

intuitivně si myslím, že “ $\ln (30) = 3, 4$, takže při 100% růstu to bude trvat 3, 4 roku. Pokud zdvojnásobím rychlost růstu, snížím potřebný čas na polovinu.“

• 100% za 3,4 roky = 1.0 * 3.4 = 3.4
• 200% na 1,7 let = 2.0 * 1.7 = 3.4
• 50% 6,8 let = 0.5 * 6.8 = 3.4
• 5% na 68 let = .05 * 68 = 3.4

Cool, co? Přirozený protokol lze použít s jakoukoli úrokovou sazbou nebo časem, pokud je jejich produkt stejný. Můžete kroutit proměnnými, jak chcete.

Úžasné příklad: Pravidlo 72

Pravidlo 72 je duševní matematika zkratka pro odhad času potřebného k zdvojnásobit své peníze. Budeme to odvodit (Jupí!) a ještě lépe to pochopíme intuitivně.

Jak dlouho trvá zdvojnásobit své peníze na 100% úrok, složený každý rok?

Uh oh. Používali jsme přirozený protokol pro nepřetržité sazby, ale teď žádáte o roční úrok? Nezkazí to náš vzorec? Ano, to bude, ale za rozumné úrokové sazby 5%, 6%, nebo dokonce 15%, tam není moc rozdíl mezi roční compounded a plně kontinuální zájem. Takže hrubý vzorec funguje, uh, zhruba a budeme předstírat, že máme plně nepřetržitý zájem.

nyní je otázka snadná: jak dlouho zdvojnásobit 100% úrok? ln (2) = .693. Chce to .693 jednotek času (roky, v tomto případě) zdvojnásobit své peníze s nepřetržitým složením se sazbou 100%.

Ok, co když náš zájem není 100% Co když je to 5% nebo 10%?

jednoduché. Tak dlouho, jak rychlost * čas = .693, zdvojnásobíme naše peníze:

• rate * time = .693
• čas = .693 / sazba

takže kdybychom měli jen 10% růst, trvalo by to .693 / .10 nebo 6,93 let na dvojnásobek.

pro zjednodušení věci vynásobme 100, takže můžeme mluvit o 10 spíše než.10:

• čas na dvojnásobek = 69,3 / sazba, kde se předpokládá sazba v procentech.

nyní je čas zdvojnásobit při 5% růstu 69,3/5 nebo 13,86 let. 69,3 však není nejvíce dělitelné číslo. Vybereme blízkého souseda, 72, který lze rozdělit na 2, 3, 4, 6, 8 a mnoho dalších čísel.

• čas na dvojnásobek = 72 / rychlost

což je pravidlo 72! V klidu.

Pokud chcete najít čas na triple, použijte ln(3) ~ 109.8 a dostat

• čas triple = 110 / cena

Což je další užitečné pravidlo. Pravidlo 72 je užitečné pro úrokové sazby, populační růst, bakteriální kultury a vše, co roste exponenciálně.

kam odtud?

doufám, že přirozený log dává větší smysl – řekne vám čas potřebný pro jakékoli množství exponenciálního růstu. Považuji to za“ přirozené“, protože e je univerzální tempo růstu, takže ln lze považovat za „univerzální“ způsob, jak zjistit, jak dlouho trvá růst.

Když uvidíte $\ln (x)$, jen si pomyslete „množství času na růst na x“. V dalším článku spojíme e a ln a sladká vůně matematiky naplní vzduch.

Dodatek: přirozený Log E

Rychlý kvíz: Co je $\ln (e)$?

• matematický robot říká: protože jsou definovány jako inverzní funkce, jasně $\ln (e) = 1$
• intuitivní člověk: ln (e) je doba potřebná k získání“ e “ jednotek růstu (asi 2.718). Ale e je množství růstu po 1 jednotce času, takže $\ln (e) = 1$.

myslete intuitivně.

Další Příspěvky V Této Sérii

1. Intuitivní Průvodce Exponenciální Funkce & e
2. Demystifikací Přirozený Logaritmus (ln)
3. Vizuální Průvodce na Jednoduché, Složené a Kontinuální Úrokové Sazby
4. Společné Definice e (Obarvené)
5. Porozumění Exponenty (Proč 0^0 = 1?)
6. Pomocí Logaritmu v Reálném Světě
7. Jak to Myslíš S Exponenty A Logaritmy
8. Porozumění Diskrétní vs. Kontinuální Růst
9. Co exponentem vážně?
10. otázka: proč je e speciální? (2.718…, ne 2, 3.7 nebo jiné číslo?)