boyleův Zákon
Robert Boyle (1627 – 1691), anglický chemik, je široce považován za jednoho ze zakladatelů moderní experimentální vědy chemie. Zjistil, že zdvojnásobení tlaku uzavřeného vzorku plynu při zachování jeho konstantní teploty způsobilo snížení objemu plynu o polovinu. Boyleův zákon uvádí, že objem dané hmotnosti plynu se mění nepřímo s tlakem, když je teplota udržována konstantní. Tímto způsobem je popsán inverzní vztah. Jak jedna proměnná zvyšuje hodnotu, druhá proměnná klesá.
fyzicky, co se děje? Molekuly plynu se pohybují a jsou v určité vzdálenosti od sebe. Zvýšení tlaku tlačí molekuly blíže k sobě a snižuje objem. Pokud je tlak snížen, plyny se mohou volně pohybovat ve větším objemu.

matematicky lze Boyleův zákon vyjádřit rovnicí:
\
\(k\) je konstanta pro daný vzorek plynu a závisí pouze na hmotnosti plynu a teplotě. Níže uvedená tabulka ukazuje údaje o tlaku a objemu pro nastavené množství plynu při konstantní teplotě. Třetí sloupec představuje hodnotu konstanty \(\left (k \right)\) pro tato data a vždy se rovná tlaku vynásobenému objemem. Jak se mění jedna z proměnných, ostatní se mění tak, že součin \(P \krát V\) zůstává vždy stejný. V tomto konkrétním případě je tato konstanta \(500 \: \ text{atm} \cdot \text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
graf z údajů v tabulce dále ukazuje inverzní vztah povahy boyleův Zákon (viz obrázek níže). Objem je vynesen na \(x\)-ose, s odpovídajícím tlakem na \(y\)-ose.
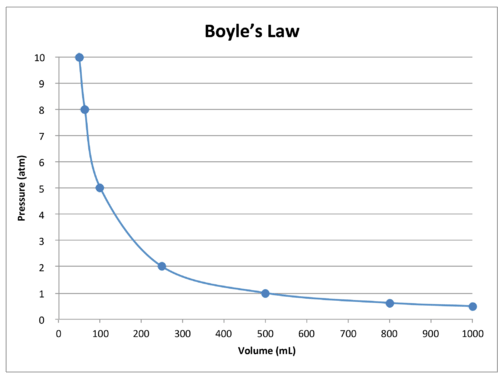
Boyleův zákon lze použít k porovnání měnících se podmínek pro plyn. Použijeme \(P_1\) a \(V_1\) pro stanovení počátečního tlaku a počátečního objemu plynu. Po provedení změny, \(P_2\) a \(V_2\) stát pro konečný tlak a objem. Matematický vztah Boyleova zákona se stává:
\
tato rovnice může být použita k výpočtu kterékoli ze čtyř veličin, pokud jsou známy další tři.
příklad \(\PageIndex{1}\)
vzorek plynného kyslíku má objem \(425 \: \text{mL}\), když je tlak roven \(387 \: \ text{kPa}\). Plyn se nechá expandovat do nádoby \(1.75 \: \ text{L}\). Vypočítejte nový tlak plynu.
řešení
Krok 1: seznam známých veličin a naplánujte problém.
Známý
- \(P_1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1.75 \: \text{L} = 1750 \: \text{mL}\)
Neznámý
- \(P_2 = ? \ : \ text{kPa}\)
použijte Boyleův zákon k vyřešení neznámého tlaku \(\left (P_2 \ right)\). Je důležité, aby dva svazky (\(V_1\) a \(V_2\)) byly vyjádřeny ve stejných jednotkách, takže \(V_2\) byl převeden na \(\text{mL}\).
Krok 2: vyřešit.
nejprve uspořádejte rovnici algebraicky tak, aby se vyřešila pro \(P_2\).
\
nyní nahraďte známé veličiny do rovnice a vyřešte.
\
Krok 3: Přemýšlejte o svém výsledku.
objem se zvýšily se mírně nad 4 násobek původní hodnoty, a tak se sníží tlak asi o čtvrtinu. Tlak je v \(\text{kPa}\) a hodnota má tři významné hodnoty. Všimněte si, že jakékoli tlakové nebo objemové jednotky lze použít, pokud jsou v celém problému konzistentní.